GEOMETRÍA

FIGURAS GEOMÉTRICAS - CURVAS

en verde: línea tangente
en azul: línea secante
en rojo: cuerda

Tangente proviene del latín «tangens»=que toca.¹​ La tangente a una curva en un punto P, es una recta que toca a la curva solo en dicho punto llamado punto de tangencia. Se puede decir que la tangente «forma un ángulo nulo» con la curva en la vecindad de dicho punto. Esta noción se puede generalizar, desde la recta tangente a un círculo o una curva, a «figuras tangentes» en dos dimensiones (es decir, figuras geométricas con un único punto de contacto, por ejemplo la circunferencia inscrita), hasta los espacios tangentes, en donde se clasifica el concepto de «tangencia» en más dimensiones.

Geometría en el plano[editar]

Recta tangente a una curva[editar]

Una recta es tangente a una curva en un punto común si en dicho punto tiene la misma pendiente que la curva. La recta tangente es un caso particular de espacio tangente a una variedad diferenciable de dimensión 1, ${\displaystyle \mathbb {R} ^{1}}$.

Construcción Geométrica[editar]

Intuitivamente, la tangente T_A es la posición límite de la recta o el límite de las rectas secantes a la curva C, que pasan por los puntos A y M_i cuando se aproximan indefinidamente por M₁, M₂, M₃, M₄ ...

Construcción analítica[editar]

Artículo principal: Derivada

Analíticamente, si C viene dada por una función f(x), tal que, ${\displaystyle A=(a,f(a))}$ y ${\displaystyle M_{i}=(m_{i},f(m_{i}))}$, entonces la recta ${\displaystyle AM_{i}}$ cuando ${\displaystyle \lim _{i\to \infty }m_{i}=a}$ tendrá como coeficiente director o pendiente:

${\displaystyle \lim _{m_{i}\to a}{\frac {f(m_{i})-f(a)}{m_{i}-a}}}$

Que por definición es ${\displaystyle f'(a)}$ la derivada de f en a.

La recta tangente, ${\displaystyle T_{A}}$, a la función es:

${\displaystyle T_{A}(x)=f'(a)(x-a)+f(a)}$

Circunferencias tangentes[editar]

Artículo principal: Problema de Apolonio

ponemos circunferencia de centro ${\displaystyle C_{i}\;}$ y radio ${\displaystyle r_{i}\;}$, es tangente en un punto ${\displaystyle P\;}$ a otra circunferencia de centro ${\displaystyle C_{j}\;}$ y radio ${\displaystyle r_{j}\;}$ si el los dos centros de las circunferencias y el punto de tangencia están sobre la misma recta, y el punto ${\displaystyle P\;}$ de tangencia es la intersección de las dos circunferencias.

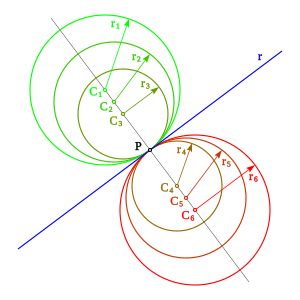
Así partiendo de una circunferencia y un punto P, de la misma, trazando una recta que pase por el centro de la circunferencia y el punto P, cualquier circunferencia con centro en esta recta, que pase por P, será tangente a la circunferencia dada en ese punto.

Circunferencia tangente a una recta[editar]

Dada una recta r y un punto P de la misma, trazando la perpendicular a la recta r por P, cualquier circunferencia con centro en esta perpendicular que pase por P es tangente a r en el punto P.

Por el razonamiento inverso podemos trazar la recta tangente a una circunferencia en un punto P dado. Su ecuación se llama ecuación de la desdoblada.

Plano tangente[editar]

Artículo principal: Espacio tangente

En geometría diferencial, espacio tangente es el conjunto asociado a cada punto de una variedad diferenciable formado por todos los vectores tangentes a dicho punto. Es un espacio vectorial de la misma dimensión que la dimensión de la variedad.

Hay varias formas de entender este concepto. Primero vamos a explicar utilizando la gráfica de al lado. Empecemos suponiendo que tenemos una curva ${\displaystyle \scriptstyle \gamma }$ en la variedad M que pasa por alguna posición elegida cualquiera: ${\displaystyle \scriptstyle x\in M}$. Es decir un mapeo ${\displaystyle \scriptstyle \gamma \ :\ ]-\varepsilon ,\varepsilon [\to M}$ diferenciableque satisface ${\displaystyle \scriptstyle \gamma (0)=x}$ y ${\displaystyle \scriptstyle \gamma '(0)=v}$. Resulta que el conjunto de todos estos vectores forman el espacio tangente ${\displaystyle \scriptstyle T_{x}M}$de x en M.

teorema de Barbier es aquel que define las características que ha de cumplir una curva para ser de longitud constante. Según el teorema, una curva es de longitud constante si su perímetro es igual a la distancia a la que se encuentran las rectas paralelas, con respecto a las que su longitud es constante, multiplicada por pi.

Este teorema fue publicado por vez primera por el astrónomo y matemático francés Joseph-Émile Barbier (1839–1889) en 1860.

Ejemplos[editar]

La circunferencia[editar]

La circunferencia es la curva de longitud constante más evidente: puede ser rotada entre dos segmentos paralelos separados por una distancia constante. La circunferencia cumple el teorema de Barbier, ya que su perímetro (π•d) es igual a la distancia que separa las paralelas multiplicadas por π, es decir π•d).

El Triángulo de Reuleaux[editar]

Trazado del triángulo Reuleaux a partir de un triángulo equilátero.

El Triángulo de Reuleaux es un caso de curva de longitud constante no tan evidente como el del círculo. La construcción de este triángulo se hace a partir de un triángulo equilátero ABC, dibujando los arcos BC usando como centro el vértice A, CA con centro en B, y AB con centro en C. Analizando el Teorema de Barbier, el valor del perímetro del Triángulo de Reuleaux es tres veces la longitud de un arco cuyo radio es la distancia entre las paralelas. Dicho arco tiene un ángulo de 60º, es decir, π/3. Por lo tanto, su perímetro es 3•(d•π/3), es decir, π•d, valor que conicide con la distancia entre las paralelas multiplicada por π (π•d).

teorema de la pelota de tenis establece que cualquier función continuamente diferenciable en la superficie de una esfera que la divide en dos zonas de igual área sin tocarse o cruzarse, debe tener al menos cuatro puntos de inflexión, puntos en los que la curva no gira localmente a un solo lado de su recta tangente.¹​

El teorema de la pelota de tenis fue publicado por primera vez con este nombre por Vladímir Arnold en 1994.²​³​ A menudo se la atribuye a Arnold, pero un resultado estrechamente relacionado aparece anteriormente en un documento de 1968 de Beniamino Segre, y el teorema de la pelota de tenis es un caso especial del teorema expuesto en un artículo de 1977 de Joel L. Weiner.⁴​⁵​ El nombre del teorema proviene de la forma estándar de una pelota de tenis, cuya costura forma una curva que cumple las condiciones del teorema; el mismo tipo de curva también se utiliza para las costuras en las bolas de béisbol.

Precisamente, un punto de inflexión de una curva doblemente diferenciable (${\displaystyle C^{2}}$) en la superficie de una esfera es un punto ${\displaystyle p}$ con la siguiente propiedad: sea ${\displaystyle I}$ el componente conexo que contiene ${\displaystyle p}$, resultado de la intersección de la curva dada con su círculo máximo tangente en ${\displaystyle p}$ (para la mayoría de las curvas, el conjunto ${\displaystyle I}$solo contendrá a ${\displaystyle p}$, pero también podría ser un arco de círculo máximo). Entonces, para que ${\displaystyle p}$ sea un punto de inflexión, cada entorno de ${\displaystyle I}$ debe contener puntos de la curva que pertenecen a ambos hemisferios separados por este círculo máximo.

El teorema establece que cada curva ${\displaystyle C^{2}}$ que divide la esfera en dos componentes de área igual tiene al menos cuatro puntos de inflexión definidos de esta manera.⁶​

Ejemplos[editar]

La pelota de tenis y las costuras de béisbol se pueden modelar matemáticamente mediante una curva hecha de cuatro arcos semicirculares, con exactamente cuatro puntos de inflexión donde se juntan los pares de estos arcos.⁷​

Un círculo máximo también biseca la superficie de la esfera, y tiene infinitos puntos de inflexión, uno en cada punto de la curva. Sin embargo, la condición de que la curva divida el área de la superficie de la esfera por igual es una parte necesaria del teorema. Otras curvas que no dividen el área por igual, como los círculos que no son círculos máximos, pueden no tener puntos de inflexión en absoluto.¹​

Prueba por acortamiento de la curva[editar]

Una prueba del teorema de la pelota de tenis es utilizar el procedimiento de la contracción de una curva, un proceso para mover continuamente los puntos de la curva hacia sus centros de curvatura local. Se puede demostrar que la aplicación de este acortamiento a la curva dada preserva la diferenciabilidad y la propiedad de dividir en dos mitades iguales el área de la curva. Además, a medida que la curva se acorta, su número de puntos de inflexión nunca aumenta. Este flujo eventualmente hace que la curva se transforme en un círculo máximo, y la convergencia a este círculo puede ser aproximada por una serie de Fourier. Debido a que el acortamiento de la curva no cambia ningún otro círculo máximo, el primer término de esta serie es cero, y si este hecho se combina con el teorema de Sturm sobre el número de ceros de la serie de Fourier, se demuestra que a medida que la curva se acerca a este círculo máximo, tiene al menos cuatro puntos de inflexión. Por lo tanto, la curva original también tiene al menos cuatro puntos de inflexión.⁸​⁹​

Teoremas relacionados[editar]

Una generalización del teorema de la pelota de tenis se aplica a cualquier curva suave y simple en la esfera que no esté contenida en un hemisferio cerrado. Al igual que en el teorema de la pelota de tenis original, dichas curvas deben tener al menos cuatro puntos de inflexión.⁵​¹⁰​ Si una curva en una esfera posee simetría central, debe tener al menos seis puntos de inflexión.¹⁰​

Un teorema estrechamente relacionado de Segre (1968) también se refiere a curvas esféricas cerradas simples. Si, para una de estas curvas, ${\displaystyle o}$ es un punto de un tramo convexo de una curva suave sobre una esfera que no es un vértice de la curva, entonces al menos cuatro puntos de la curva poseen un plano osculador que pasa por ${\displaystyle o}$. En particular, para una curva no contenida en un hemisferio, este teorema se puede aplicar con ${\displaystyle o}$ en el centro de la esfera. Cada punto de inflexión de una curva esférica tiene un plano de osculación que pasa a través del centro de la esfera, pero esto también podría ser cierto para algunos otros puntos.⁴​⁵​

Este teorema es análogo al teorema de los cuatro vértices, dado que cada curva de Jordan suave en el plano tiene cuatro vértices (puntos extremos de curvatura). También es análogo a un teorema de August Möbius, en el que se afirma que cada curva suave no contraíble en el plano proyectivo tiene al menos tres puntos de inflexión.