PROBLEMAS MATEMÁTICOS

Claude Gaspard Bachet de Méziriac, matemático francés, escribió el primer tratado de matemáticas recreativasde que se tenga noticia.

Su obra titulada Entretenidos problemas que se plantean con los números fue publicada en 1612 y fue en ella donde Bachet propuso el problema de las pesas, cuyo enunciado es el siguiente:

Un mercader tenía una pesa de 40 kg que al caer al piso se rompió y se dividió en cuatro partes desiguales. Llevó estos pesos a una balanza y comprobó que cada uno tenía un peso que era igual a un número entero de kilogramos y al emplearlas para pesar observó que con estas cuatro pesas podía pesar cargas de objetos cuyo peso fuera un número entero cualquiera de kilogramos entre 1 y 40. ¿Cuántos kilogramos pesa cada una de las cuatro pesas?

Soluciones[editar]

La solución dada por Bachet es la siguiente: tenemos en primer lugar que los objetos que se van a pesar tienen un peso entero de kilogramos. Llámese a uno de los platillos de la balanza, platillo de las pesas y al otro platillo de las cargas. Una cuestión importante es que las pesas pueden colocarse en ambos platillos, esto es, tanto en el de las pesas como en el de las cargas. Por ejemplo con dos pesas, una de 1 kg y otra de 3 kg se pueden realizar las siguientes pesadas:

Platillo de las cargas	Platillo de las pesas	Total pesada
--	1 kg	1 kg
1 kg	3 kg	2 kg
--	3 kg	3 kg
--	1 kg y 3 kg	4 kg

Sean A, B, C... un conjunto dado de pesas y supóngase que adecuadamente distribuidas se pueden pesar con ellas objetos que pesen desde 1 kg hasta n kg. Sea P una nueva pesa cuyo peso p sea tal que excede al peso total n de las pesas dadas en n+1 kg; es decir, p - n = n + 1, o sea p = 2 n + 1. Obsérvese también que ahora será posible pesar los objetos dados, desde un 1 kg hasta p + n = 3n + 1, si a las pesas A, B, C... le añadimos la pesa P.

Como con el conjunto dado A, B, C... se pueden pesar objetos cuyos pesos varíen desde 1 kg hasta n kg, entonces para pesar un objeto cuyo peso sea:

(p + x) kg o (p - x) kg; 0 < x < n

Se colocará la pesa P en el platillo de las pesas y se distribuirán las pesas A, B, C... entre ambos platillos, hasta lograr que las últimas pesas ofrezcan a uno de los dos platillos un exceso de x kg. Entonces se ve fácilmente que si solo tenemos dos pesas, y se quiere pesar entre las posibles cargas de 1 a 40 kg los objetos menos pesados, se podrá considerar que la pesa A sea de 1 kg y la otra B sea de 3 kg. De este modo, se podrán pesar objetos con pesos de 1 kg, 2 kg, 3 kg y 4 kg.

Si se selecciona una tercera pesa C, de modo que su peso c sea c = 2n + 1, se tiene:

c = 2 × 4 + 1 = 9 kg.

Así, con las pesas A, B y C se pueden pesar objetos desde 1 kg hasta C + 4 = 9 + 4 = 13 kg.

Si se toma finalmente, la cuarta pesa D, porción más pesada de la pesa rota, su peso será:

d = 2 × 13 + 1 = 27 kg.

De este modo, las cuatro pesas que se formaron al dividirse la pesa dada; es decir, A, B, C y D permiten pesar cargas que van desde 1 kg hasta:

27 + 13 = 3 × 13 + 1 = 40 kg.

Por tanto las cuatro pesas que se formarán al dividirse la pesa dada son: 1, 3, 9 y 27 kg.

El problema del mono y los cocos es un problema de álgebra recreativa en cuya resolución se emplean típicamente ecuaciones diofánticas.

Enunciado[editar]

El enunciado de este problema es el siguiente: Cinco hombres y un mono naufragan en una isla desierta. Los hombres pasan todo el primer día recogiendo cocos. Por la noche, uno de ellos despierta y, desconfiado, decide separar su parte. Divide los cocos en cinco montones, toma su parte y, como sobra un coco, se lo da al mono. Poco después, un segundo náufrago se despierta y hace lo mismo. Al dividir los cocos en cinco montones, vuelve a sobrar un coco y también se lo da al mono. Uno tras otro, el tercero, cuarto y quinto náufragos hacen lo mismo. Al día siguiente por la mañana, dividen los cocos en cinco montones sin que sobre ninguno. ¿Cuántos se habían recolectado inicialmente?

Una variación de este planteamiento es que en el reparto final sobra un coco en lugar de no sobrar ninguno.

Planteamiento[editar]

El planteamiento algebraico del problema es de relativa sencillez. Representando por X_i {i = 1...5} al número de cocos que toma cada uno de los náufragos y X₆ el total de las existencias, se origina el siguiente sistema de ecuaciones:

${\displaystyle \left\{{\begin{array}{rcr}X_{6}&=&5X_{1}+1\\4X_{1}&=&5X_{2}+1\\4X_{2}&=&5X_{3}+1\\4X_{3}&=&5X_{4}+1\\4X_{4}&=&5X_{5}+1\end{array}}\right|\quad \longrightarrow \quad \left\{{\begin{array}{rrrrrrcr}-5X_{1}&&&&&+X_{6}&=&1\\4X_{1}&-5X_{2}&&&&&=&1\\&4X_{2}&-5X_{3}&&&&=&1\\&&4X_{3}&-5X_{4}&&&=&1\\&&&4X_{4}&-5X_{5}&&=&1\end{array}}\right.}$

Con las restricciones adicionales:

Para todo X_i Entero; para todo X_i > 0

Obligando a que el número de cocos ha de estar expresado por un número natural.

El sistema anterior constituye un claro ejemplo de ecuaciones diofánticas para las que no se conoce un algoritmode resolución sistemática. No obstante, es de relativa sencillez mediante procedimientos informáticos usuales.

Tratamiento informático[editar]

Esta clase de problemas se prestan a una representación matricial muy compacta, que facilita la resolución posterior.

FIGURA I

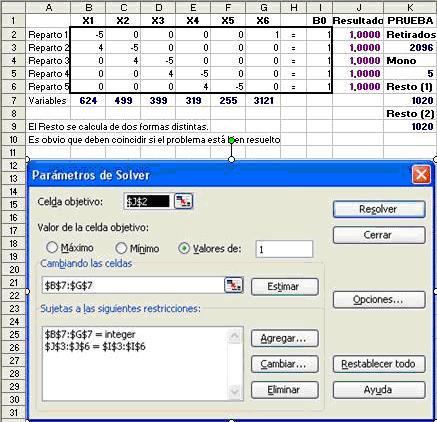
La Figura I es una imagen de la "Hoja de Cálculo" utilizada. La parte superior corresponde al planteamiento del problema para su tratamiento matemático. En el inferior se ha copiado la pantalla propia del "Solver", donde puede apreciarse la estructura típica de esta clase de problemas, formada por:

• Función objetivo.
• Variables.
• Restricciones.

El manejo del programa es sencillo, variando en algunos detalles según fabricantes. En el aquí representado, una segunda pantalla permite refinar el tratamiento matemático más adecuado a cada situación

Resultado[editar]

Por último, el resultado obtenido ha sido:

${\displaystyle {\begin{array}{rcr}X_{1}&=&624\\X_{2}&=&499\\X_{3}&=&399\\X_{4}&=&319\\X_{5}&=&255\\X_{6}&=&3121\end{array}}}$