el algoritmo de antepasados comunes más bajos fuera de línea de Tarjan es un algoritmopara calcular los antepasados comunes más bajos para pares de nodos en un árbol, basado en la estructura de datos de búsqueda de unión . El antepasado común más bajo de dos nodos d y e en un árbol con raíz T es el nodo g que es un antepasado de ambos d y e y que tiene la mayor profundidad en T . Lleva el nombre de Robert Tarjan, quien descubrió la técnica en 1979. El algoritmo de Tarjan es un algoritmo fuera de línea; es decir, a diferencia de otros algoritmos de antepasados comunes más bajos, requiere que todos los pares de nodos para los que se desea el antepasado común más bajo se especifiquen de antemano. La versión más simple del algoritmo usa la estructura de datos de búsqueda de unión, que a diferencia de otras estructuras de datos de antepasados comunes más bajas puede tomar más tiempo constante por operación cuando el número de pares de nodos es similar en magnitud al número de nodos. Un refinamiento posterior de Gabow y Tarjan (1983)acelera el algoritmo hasta el tiempo lineal .
Pseudocódigo [ editar ]
El pseudocódigo siguiente determina el antepasado común más bajo de cada par en P , dada la raíz r de un árbol en el que los hijos del nodo n están en el conjunto n.children . Para este algoritmo fuera de línea, el conjunto Pdebe especificarse por adelantado. Utiliza las funciones MakeSet , Find y Union de un bosque de conjuntos disjuntos . MakeSet (u) elimina u a un conjunto único, Find (u) devuelve el representante estándar del conjunto que contiene u , y Union (u, v) fusiona el conjunto que contiene ucon el conjunto que contiene v . TarjanOLCA ( r ) se llama por primera vez en la raíz r .
función TarjanOLCA (u) MakeSet (u); u.ancestor: = u; para cada v en u.children do TarjanOLCA (v); Unión (u, v); Encuentra (u) .ancestor: = u; u.color: = negro; para cada v tal que {u, v} en P haga si v.color == negro Imprimir "El antepasado común más bajo de Tarjan" + u + "y" + v + "es" + Find (v) .ancestor + ".";
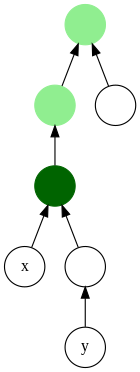
Cada nodo es inicialmente blanco y tiene un color negro después de él y todos sus hijos han sido visitados. El antepasado común más bajo del par {u, v} está disponible como Find (v) .ancestor inmediatamente (y solo inmediatamente) después de que u sea de color negro, siempre que v ya sea negro. De lo contrario, estará disponible más adelante como Find (u) .ancestor , inmediatamente después de que v sea de color negro.
Para referencia, aquí están las versiones optimizadas de MakeSet , Find y Union para un bosque de conjuntos disjuntos :
función MakeSet (x) x.parent: = x x.rank: = 1 funcion union (x, y) xRoot: = Buscar (x) yRoot: = Buscar (y) si xRoot.rank> yRoot.rank yRoot.parent: = xRoot de lo contrario si xRoot.rankxRoot.parent: = yRoot más si xRoot.rank == yRoot.rank yRoot.parent: = xRoot xRoot.rank: = xRoot.rank + 1 función Buscar (x) si x.parent! = x x.parent: = Buscar (x.parent) volver x.parent
Este artículo trata sobre los antepasados comunes más bajos en teoría de grafos y ciencias de la computación. Para el ancestro común de un conjunto de especies en árboles evolutivos, vea el ancestro común más reciente . Para un antepasado común de todas las formas de vida, vea el último ancestro común universal .
En teoría de gráficos y ciencias de la computación , el antepasado común más bajo( LCA ) de dos nodos v y w en un árbol o gráfico acíclico dirigido (DAG) T es el nodo más bajo (es decir, el más profundo) que tiene tanto v y w como descendientes, donde Defina que cada nodo sea un descendiente de sí mismo (por lo tanto, si v tiene una conexión directa desde w , w es el antepasado común más bajo).
El LCA de v y w en T es el ancestro compartido de v y w que se encuentra más alejado de la raíz. El cálculo de los antepasados comunes más bajos puede ser útil, por ejemplo, como parte de un procedimiento para determinar la distancia entre pares de nodos en un árbol: la distancia de v a w se puede calcular como la distancia de la raíz a v , más la distancia desde la raíz hasta w , menos el doble de la distancia desde la raíz hasta su ancestro común más bajo ( Djidjev, Pantziou y Zaroliagis, 1991). En ontologías , el antepasado común más bajo también se conoce comoantepasado menos común .
En una estructura de datos de árbol donde cada nodo apunta a su padre, el ancestro común más bajo puede determinarse fácilmente encontrando la primera intersección de las rutas de v y w a la raíz. En general, el tiempo de cálculo requerido para este algoritmo es O (h) donde h es la altura del árbol (longitud de la ruta más larga desde una hoja hasta la raíz). Sin embargo, existen varios algoritmos para procesar árboles para que los ancestros comunes más bajos se puedan encontrar más rápidamente. El algoritmo de antepasados comunes más bajos fuera de línea de Tarjan , por ejemplo, preprocesa un árbol en tiempo lineal para proporcionar consultas LCA de tiempo constante. En los DAG generales, existen algoritmos similares, pero con una complejidad súper lineal.
Historia [ editar ]
Alfred Aho , John Hopcroft y Jeffrey Ullman ( 1973 ) definieron el problema de los antepasados comunes más bajos , pero Dov Harel y Robert Tarjan ( 1984 ) fueron los primeros en desarrollar una estructura de datos de antepasados comunes más bajos de la manera más eficiente. Su algoritmo procesa cualquier árbol en tiempo lineal, utilizando una descomposición de ruta pesada , de modo que las siguientes consultas de antepasados comunes más bajas puedan responderse en tiempo constante por consulta. Sin embargo, su estructura de datos es compleja y difícil de implementar. Tarjan también encontró un algoritmo más simple pero menos eficiente, basado en la estructura de datos de union-find , paracalcular los antepasados comunes más bajos de un lote fuera de línea de pares de nodos .
Baruch Schieber y Uzi Vishkin ( 1988 ) simplificaron la estructura de datos de Harel y Tarjan, lo que llevó a una estructura implementable con los mismos límites de tiempo de consulta y preprocesamiento asintóticos. Su simplificación se basa en el principio de que, en dos tipos especiales de árboles, los antepasados comunes más bajos son fáciles de determinar: si el árbol es una ruta, entonces el antepasado común más bajo se puede calcular simplemente desde el mínimo de los niveles de los dos consultados. Nodos, mientras que si el árbol es un árbol binario completo.Los nodos pueden indexarse de tal manera que los antepasados comunes más bajos se reduzcan a simples operaciones binarias en los índices. La estructura de Schieber y Vishkin descompone cualquier árbol en una colección de caminos, de manera que las conexiones entre los caminos tienen la estructura de un árbol binario y combinan estas dos técnicas de indexación más simples.
Omer Berkman y Uzi Vishkin ( 1993 ) descubrieron una forma completamente nueva de responder a las consultas de antepasados comunes más bajas, logrando nuevamente un tiempo de preprocesamiento lineal con tiempo de consulta constante. Su método consiste en formar un recorrido de Euler de un gráfico formado a partir del árbol de entrada al duplicar cada borde, y usar este recorrido para escribir una secuencia de números de nivel de los nodos en el orden en que el recorrido los visita; una consulta de antepasado común más baja puede luego transformarse en una consulta que busca el valor mínimo que ocurre dentro de algún subintervalo de esta secuencia de números. Entonces manejan este rango mínimo de consulta.problema al combinar dos técnicas, una técnica basada en la precomputación de las respuestas a intervalos grandes que tienen tamaños que tienen potencias de dos y la otra basada en la búsqueda de tablas para consultas de intervalos pequeños. Este método fue presentado más tarde en una forma simplificada por Michael Bender y Martin Farach-Colton ( 2000 ). Como se observó anteriormente en Gabow, Bentley y Tarjan (1984) , el problema del rango mínimo puede a su vez transformarse nuevamente en un problema común más bajo de antepasados utilizando la técnica de los árboles cartesianos .
Una variante del problema es el problema LCA dinámico en el que la estructura de datos debe estar preparada para manejar consultas LCA entremezcladas con operaciones que cambian el árbol (es decir, reorganizar el árbol agregando y eliminando bordes). Esta variante se puede resolver utilizando O ( logN) tiempo para todas las modificaciones y consultas. Esto se hace manteniendo el bosque utilizando la estructura de datos de árboles dinámicos con particiones por tamaño; esto mantiene una descomposición de cada árbol, y permite que las consultas de LCA se realicen en tiempo logarítmico en el tamaño del árbol.
Sin el preprocesamiento, también puede mejorar el tiempo de cálculo del algoritmo en línea ingenuo a O (registro h ) almacenando las rutas a través del árbol utilizando listas de acceso aleatorio sesgado-binario, mientras que permite que el árbol se amplíe en tiempo constante ( Edward Kmett (2012) ). Esto permite que las consultas de LCA se realicen en tiempo logarítmico en la altura del árbol.
Extensión a gráficos acíclicos dirigidos [ editar ]
Aunque se estudió originalmente en el contexto de los árboles, la noción de antepasados comunes más bajos se puede definir para los gráficos acíclicos dirigidos (DAG), utilizando cualquiera de las dos definiciones posibles. En ambos, se asume que los bordes del DAG apuntan de padres a hijos.
- Dado G = ( V , E ) , Aït-Kaci et al. (1989) definen un poset ( V , ≤) tal que x ≤ y si f x está en el cierre transitivo reflexivo de y . Los antepasados comunes más bajos de x e y son los elementos mínimos bajo ≤ del conjunto de antepasados comunes { z ∈ V | x ≤ z y y ≤ z }.
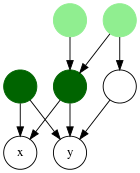
- Bender et al. (2005) dieron una definición equivalente, donde los antepasados comunes más bajos de x e y son los nodos de grado cero en el subgrafo de Ginducidos por el conjunto de ancestros comunes de x e y .
En un árbol, el antepasado común más bajo es único; en un DAG de n nodos, cada par de nodos puede tener tanto como n -2 LCA ( Bender et al. 2005 ), mientras que la existencia de un LCA para un par de nodos ni siquiera está garantizada en DAG conectados arbitrariamente.
Un algoritmo de fuerza bruta para encontrar los antepasados comunes más bajos está dado por Aït-Kaci et al. (1989) : encuentra todos los ancestros de x e y , luego devuelve el elemento máximo de la intersección de los dos conjuntos. Existen mejores algoritmos que, de forma análoga a los algoritmos de LCA en los árboles, preprocesan una gráfica para permitir consultas de LCA de tiempo constante. El problema de la existencia de LCA se puede resolver de manera óptima para DAG dispersos mediante un algoritmo O (| V || E |) debido a Kowaluk y Lingas (2005) .
Dash et al. (2013) presentan un marco unificado para el preprocesado de gráficos acíclicos dirigidos (DAG) para calcular el límite inferior mínimo de dos vértices en tiempo constante. Su marco utiliza un preprocesamiento adaptativo en el que los costos asintóticos dependen del número de bordes (cruzados) que no son de árbol en el DAG. En consecuencia, es posible lograr tiempos de procesamiento previo casi lineales para DAG dispersos con búsquedas de LCA de tiempo constante. Una biblioteca de su trabajo está disponible para uso público en. [1]
Couto et al. (2011) presentan a DiShIn un método que extiende el cálculo del LCA a todos los ancestros disyuntivos en medidas de similitud semántica. Define a un antepasado como disyuntivo si la diferencia entre el número de rutas distintas de los dos nodos a ese antepasado es diferente de usar cualquier antepasado común inferior.
Aplicaciones [ editar ]
El problema de computar los antepasados comunes más bajos de clases en una jerarquía de herencia surge en la implementación de sistemas de programación orientados a objetos ( Aït-Kaci et al. 1989 ). El problema de LCA también encuentra aplicaciones en modelos de sistemas complejos que se encuentran en la computación distribuida ( Bender et al. 2005 ).
ordenamiento topológico o ordenamiento topológico de un gráfico dirigidoes un ordenamiento lineal de sus vértices, de modo que para cada borde dirigido uv desde el vértice u al vértice v, u aparece antes de v en el ordenamiento. Por ejemplo, los vértices del gráfico pueden representar tareas a realizar, y los bordes pueden representar restricciones de que una tarea debe realizarse antes que otra; en esta aplicación, un ordenamiento topológico es solo una secuencia válida para las tareas. Un ordenamiento topológico es posible si y solo si el gráfico no tieneCiclos dirigidos , es decir, si se trata de un gráfico acíclico dirigido (DAG). Cualquier DAG tiene al menos un ordenamiento topológico, y se conocen algoritmos para construir un ordenamiento topológico de cualquier DAG en tiempo lineal .
Ejemplos [ editar ]
La aplicación canónica de la clasificación topológica consiste en programar una secuencia de trabajos o tareas en función de sus dependencias . Los trabajos están representados por vértices, y hay un borde de x a y si el trabajo x debe completarse antes de que pueda comenzar el trabajo y (por ejemplo, al lavar la ropa, la lavadora debe terminar antes de poner la ropa en la secadora) . Luego, un ordenamiento topológico da un orden en el que realizar los trabajos. Una aplicación estrechamente relacionada de los algoritmos de clasificación topológica se estudió por primera vez a principios de la década de 1960 en el contexto de la técnica PERT para la programación en la gestión de proyectos ( Jarnagin 1960); en esta aplicación, los vértices de un gráfico representan los hitos de un proyecto, y los bordes representan tareas que deben realizarse entre un hito y otro. La clasificación topológica forma la base de los algoritmos de tiempo lineal para encontrar la ruta crítica del proyecto, una secuencia de hitos y tareas que controlan la duración del cronograma general del proyecto.
En ciencias de la computación, las aplicaciones de este tipo surgen en la programación de instrucciones , el ordenamiento de la evaluación de la celda de fórmula cuando se vuelven a calcular los valores de fórmula en las hojas de cálculo , la síntesis lógica , la determinación del orden de las tareas de compilación a realizar en los archivos make , la serialización de datos y la resolución de dependencias de símbolos en los vinculadores . También se utiliza para decidir en qué orden cargar tablas con claves externas en las bases de datos.
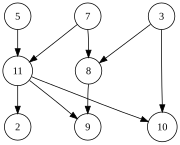
La gráfica que se muestra a la izquierda tiene muchos tipos topológicos válidos, que incluyen:
- 5, 7, 3, 11, 8, 2, 9, 10 (visual de izquierda a derecha, de arriba a abajo)
- 3, 5, 7, 8, 11, 2, 9, 10 (vértice disponible con el número más pequeño primero)
- 5, 7, 3, 8, 11, 10, 9, 2 (el menor número de bordes primero)
- 7, 5, 11, 3, 10, 8, 9, 2 (el vértice más grande disponible primero)
- 5, 7, 11, 2, 3, 8, 9, 10 (intentando de arriba a abajo, de izquierda a derecha)
- 3, 7, 8, 5, 11, 10, 2, 9 (arbitrario)
Algoritmos [ editar ]
Los algoritmos habituales para la clasificación topológica tienen un tiempo de ejecución lineal en el número de nodos más el número de bordes, asintóticamente, 
El algoritmo de Kahn [ editar ]
Uno de estos algoritmos, descrito por primera vez por Kahn (1962) , funciona al elegir vértices en el mismo orden que el ordenamiento topológico eventual. Primero, busque una lista de "nodos de inicio" que no tengan bordes entrantes e insértelos en un conjunto S; al menos uno de estos nodos debe existir en un gráfico acíclico no vacío. Entonces:
L ← Lista vacía que contendrá los elementos ordenados.
S ← Conjunto de todos los nodos sin borde entrante
mientras que S no es vacío hacer
eliminar un nodo n de S
agregue n a la cola de L
para cada nodo m con un borde e de n a m do
quitar el borde e de la gráfica
si m no tiene otros bordes entrantes entonces
inserte m en S
si el gráfico tiene aristas ,
devuelva el error (el gráfico tiene al menos un ciclo)
o
devuelva L (un orden ordenado topológicamente)
Si la gráfica es un DAG , una solución estará contenida en la lista L (la solución no es necesariamente única). De lo contrario, la gráfica debe tener al menos un ciclo y, por lo tanto, una clasificación topológica es imposible.
Reflejando la no singularidad de la clasificación resultante, la estructura S puede ser simplemente un conjunto o una cola o una pila. Dependiendo del orden en que los nodos n se eliminan del conjunto S, se crea una solución diferente. Una variación del algoritmo de Kahn que rompe los lazos lexicográficamente forma un componente clave del algoritmo de Coffman-Graham para la programación paralela y el dibujo de gráficos en capas .
Búsqueda en profundidad primero [ editar ]
Un algoritmo alternativo para la clasificación topológica se basa en la búsqueda en profundidad . El algoritmo recorre cada nodo de la gráfica, en un orden arbitrario, iniciando una búsqueda en profundidad que termina cuando llega a cualquier nodo que ya ha sido visitado desde el principio de la clasificación topológica o el nodo no tiene bordes salientes (es decir, un nodo). nodo de la hoja):
L ← Lista vacía que contendrá los nodos ordenados
mientras haya nodos sin una marca permanente .
seleccione un nodo sin marcar n
visita (n)
visita de la función (nodo n)
si n tiene una marca permanente, luego regrese
si n tiene una marca temporal y luego se detiene (no un DAG)
marca n con una marca temporal
para cada nodo m con un borde de n a m hacer
visita (m)
quitar marca temporal de n
marca n con una marca permanente
añadir n a la cabeza de L
Cada nodo n se añade a la lista de salida L solo después de considerar todos los demás nodos que dependen de n (todos los descendientes de n en el gráfico). Específicamente, cuando el algoritmo agrega el nodo n , se garantiza que todos los nodos que dependen de n ya están en la lista de salida L: fueron agregados a L bien por la llamada recursiva a visit () que terminó antes de la llamada a visit n , o por una llamada a visitar () que comenzó incluso antes de la llamada a visitar n . Dado que cada borde y nodo se visitan una vez, el algoritmo se ejecuta en tiempo lineal. Este algoritmo basado en la búsqueda en profundidad es el descrito por Cormen et al. (2001); Parece haber sido descrito por primera vez en forma impresa por Tarjan (1976) .
Algoritmos paralelos [ editar ]
En una máquina paralela de acceso aleatorio , se puede construir un ordenamiento topológico en tiempo O (log 2n ) utilizando un número polinomial de procesadores, lo que coloca el problema en la clase de complejidad NC 2 ( Cook 1985 ). Un método para hacer esto es cuadrar repetidamente la matriz de adyacencia de la gráfica dada, logarítmicamente muchas veces, usando la multiplicación de la matriz de mínimo más con la maximización en lugar de la minimización. La matriz resultante describe las distancias de camino más largas en el gráfico. La clasificación de los vértices por la longitud de sus caminos de entrada más largos produce un ordenamiento topológico ( Dekel, Nassimi y Sahni 1981).
Aplicación para encontrar el camino más corto [ editar ]
El ordenamiento topológico también se puede usar para calcular rápidamente las rutas más cortas a través de un gráfico acíclico dirigido ponderado . Sea V la lista de vértices en tal gráfica, en orden topológico. A continuación, el siguiente algoritmo calcula la ruta más corta desde alguna fuente vértice s a todos los otros vértices: [1]
- Sea d una matriz de la misma longitud que V ; esto mantendrá las distancias de recorrido más cortas desde s . Establezca d [ s ] = 0 , todos los demás d [ u ] = ∞ .
- Sea p una matriz de la misma longitud que V , con todos los elementos inicializados a cero . Cada p [ u ] mantendrá al predecesor de u en el camino más corto de s a u .
- Recorre los vértices u ordenados en V , comenzando desde s :
- Para cada vértice v que sigue directamente a u (es decir, existe un borde de u a v ):
- Sea w el peso del borde de u a v .
- Relaje el borde: si d [ v ]> d [ u ] + w , establezca
- d [ v ] ← d [ u ] + w ,
- p [ v ] ← u .
En una gráfica de n vértices y m bordes, este algoritmo toma Θ ( n + m ) , es decir, lineal , tiempo. [1]
Unicidad [ editar ]
Si una ordenación topológica tiene la propiedad de que todos los pares de vértices consecutivos en el orden ordenado están conectados por bordes, estos bordes forman un camino hamiltoniano dirigido en el DAG . Si existe una ruta hamiltoniana, el ordenamiento topológico es único; Ningún otro orden respeta los bordes del camino. A la inversa, si un ordenamiento topológico no forma una ruta hamiltoniana, el DAG tendrá dos o más ordenamientos topológicos válidos, ya que en este caso siempre es posible formar un segundo ordenamiento válido intercambiando dos vértices consecutivos que no están conectados por un borde el uno al otro Por lo tanto, es posible probar en tiempo lineal si existe una ordenación única, y si existe una ruta hamiltoniana, a pesar de la dureza NPdel problema de la trayectoria hamiltoniana para gráficos dirigidos más generales ( Vernet y Markenzon 1997 ).
Relación con órdenes parciales [ editar ]
Los ordenamientos topológicos también están estrechamente relacionados con el concepto de una extensión lineal de un orden parcial en matemáticas. En términos de alto nivel, hay un complemento entre los gráficos dirigidos y las órdenes parciales. [2]
Un conjunto parcialmente ordenado es solo un conjunto de objetos junto con una definición de la relación de desigualdad "≤", que satisface los axiomas de reflexividad ( x ≤ x ), antisimetría (si x ≤ y y y ≤ x entonces x = y ) y transitividad (Si x ≤ y y y ≤ z , entonces x ≤ z ). Un orden total es un orden parcial en el que, por cada dos objetos x e y en el conjunto, ya sea x ≤ y o y ≤ x . Los pedidos totales son familiares en informática, ya que los operadores de comparación necesarios para realizar algoritmos de clasificación de comparación . Para conjuntos finitos, los pedidos totales pueden identificarse con secuencias lineales de objetos, donde la relación "≤" es verdadera siempre que el primer objeto precede al segundo objeto en el orden; de este modo se puede usar un algoritmo de clasificación de comparación para convertir un orden total en una secuencia. Una extensión lineal de un orden parcial es un orden total que es compatible con él, en el sentido de que, si x ≤ y en el orden parcial, entonces x ≤ y también en el orden total.
Uno puede definir un orden parcial de cualquier DAG dejando que el conjunto de objetos sean los vértices del DAG, y definiendo x ≤ y para que sea verdadero, para cualquiera de los dos vértices x e y , siempre que exista una ruta dirigida de x a y ; es decir, siempre que y sea accesible desde x. Con estas definiciones, un ordenamiento topológico del DAG es lo mismo que una extensión lineal de este orden parcial. A la inversa, cualquier orden parcial en un conjunto finito puede definirse como la relación de accesibilidad en un DAG. Una forma de hacerlo es definir un DAG que tenga un vértice para cada objeto en el conjunto parcialmente ordenado, y un borde xy para cada par de objetos para los cuales x ≤ y . Una forma alternativa de hacer esto es usar la reducción transitiva del ordenamiento parcial; en general, esto produce DAG con menos aristas, pero la relación de accesibilidad en estos DAG sigue siendo el mismo orden parcial. Al usar estas construcciones, uno puede usar algoritmos de ordenamiento topológico para encontrar extensiones lineales de órdenes parciales.
No hay comentarios:
Publicar un comentario