LISTAS RELACIONADAS CON LAS MATEMÁTICAS - ALGORITMOS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Una gráfica y dos de sus cortes. La línea de puntos en rojo es un corte con tres bordes que se cruzan. La línea discontinua en verde es un corte mínimo de este gráfico, que solo cruza dos bordes.

En informática y teoría de gráficos , el algoritmo de Karger es un algoritmo aleatorio para calcular un corte mínimo de un gráficoconectado . Fue inventado por David Karger y publicado por primera vez en 1993. ^[1]

La idea del algoritmo se basa en el concepto de contracción de un borde.$${\ displaystyle (u, v)} en un grafo no dirigido $${\ displaystyle G = (V, E)}. Hablando de manera informal, la contracción de un borde fusiona los nodos.$${\ displaystyle u} y $${\ displaystyle v}en uno, reduciendo el número total de nodos del gráfico en uno. Todos los otros bordes que conectan$${\ displaystyle u} o $${\ displaystyle v}se "vuelven a unir" al nodo combinado, produciendo efectivamente un multigraph . El algoritmo básico de Karger contrae iterativamente bordes elegidos al azar hasta que solo quedan dos nodos; Esos nodos representan un corte en la gráfica original. Al iterar este algoritmo básico un número suficiente de veces, se puede encontrar un corte mínimo con alta probabilidad.

El problema de corte mínimo global [ editar ]

Artículo principal: Corte mínimo

Un corte $${\ displaystyle (S, T)} en un grafo no dirigido $${\ displaystyle G = (V, E)} Es una partición de los vértices. $${\ displaystyle V} en dos conjuntos no vacíos, desunidos $${\ displaystyle S \ cup T = V}. El cutset de un corte consiste en los bordes.$${\ displaystyle \ {\, uv \ en E \ colon u \ en S, v \ en T \, \}}entre las dos partes. El tamaño (o peso ) de un corte en un gráfico no ponderado es la cardinalidad del cutset, es decir, el número de bordes entre las dos partes,

$${\ displaystyle w (S, T) = | \ {\, uv \ en E \ colon u \ en S, v \ en T \, \} | \ ,.}

Existen $${\ displaystyle 2 ^ {| V |}} Formas de elegir para cada vértice si pertenece a $${\ displaystyle S} o para $${\ displaystyle T}, pero dos de estas elecciones hacen $${\ displaystyle S} o $${\ displaystyle T}Vacíos y no dan lugar a cortes. Entre las opciones restantes, intercambiar los roles de$${\ displaystyle S} y $${\ displaystyle T}no cambia el corte, por lo que cada corte se cuenta dos veces; por lo tanto, hay$${\ displaystyle 2 ^ {| V | -1} -1}distintos cortes. El problema de corte mínimo es encontrar un corte de tamaño más pequeño entre estos cortes.

Para gráficos ponderados con ponderaciones de borde positivas. $${\ displaystyle w \ colon E \ rightarrow \ mathbf {R} ^ {+}} El peso del corte es la suma de los pesos de los bordes entre vértices en cada parte.

$${\ displaystyle w (S, T) = \ sum _ {uv \ en E \ colon u \ en S, v \ en T} w (uv) \ ,,}

que concuerda con la definición no ponderada de $${\ displaystyle w = 1}.

Un corte a veces se denomina "corte global" para distinguirlo de un "corte global".$${\ displaystyle s}-$${\ displaystyle t} cortar ”para un par de vértices dado, que tiene el requisito adicional de que $${\ displaystyle s \ en S} y $${\ displaystyle t \ in T}. Cada corte global es un$${\ displaystyle s}-$${\ displaystyle t} cortar para algunos $${\ displaystyle s, t \ en V}. Por lo tanto, el problema de corte mínimo se puede resolver en tiempo polinomial mediante la iteración de todas las opciones de$${\ displaystyle s, t \ en V} y resolviendo el mínimo resultante. $${\ displaystyle s}-$${\ displaystyle t}problema de corte usando el teorema de corte mínimo de flujo máximo y un algoritmo de tiempo polinomial para el flujo máximo , como el algoritmo push-reetiquetado , aunque este enfoque no es óptimo. Los mejores algoritmos deterministas para el problema de corte mínimo global incluyen el algoritmo Stoer-Wagner , que tiene un tiempo de ejecución de$${\ displaystyle O (mn + n ^ {2} \ log n)}. ^[2]

Algoritmo de contracción [ editar ]

La operación fundamental del algoritmo de Karger es una forma de contracción del borde . El resultado de contraer el borde.$${\ displaystyle e = \ {u, v \}} es nuevo nodo $${\ displaystyle uv}. Cada borde$${\ displaystyle \ {w, u \}} o $${\ displaystyle \ {w, v \}} para $${\ displaystyle w \ notin \ {u, v \}} a los puntos finales del borde contratado se sustituye por un borde $${\ displaystyle \ {w, uv \}}al nuevo nodo. Finalmente, los nodos contratados.$${\ displaystyle u} y $${\ displaystyle v}Con todos sus bordes incidentes se eliminan. En particular, el gráfico resultante no contiene auto-bucles. El resultado de la contratación de ventaja.$${\ displaystyle e} se denota $${\ displaystyle G / e}.

El algoritmo de contracción contrata repetidamente bordes aleatorios en el gráfico, hasta que solo quedan dos nodos, momento en el que solo hay un corte único.

Ejecución exitosa del algoritmo de Karger en un gráfico de 10 vértices. El corte mínimo tiene tamaño 3.

   contrato de trámite ($${\ displaystyle G = (V, E)}
  
):
    mientras {\ displaystyle | V |> 2}
  

       escoger $${\ displaystyle e \ en E}
  
 uniformemente al azar
       $${\ displaystyle G \ leftarrow G / e}
  

   devuelve el único corte en$${\ displaystyle G}
  

Cuando el gráfico se representa mediante listas de adyacencia o una matriz de adyacencia , se puede implementar una única operación de contracción de borde con un número lineal de actualizaciones a la estructura de datos, para un tiempo total de ejecución de$${\ displaystyle O (| V | ^ {2})}. Alternativamente, el procedimiento se puede ver como una ejecución del algoritmo de Kruskal para construir el árbol de expansión mínimo en un gráfico donde los bordes tienen pesos$${\ displaystyle w (e_ {i}) = \ pi (i)} de acuerdo con una permutación aleatoria $${\ displaystyle \ pi}. Eliminar el borde más pesado de este árbol da como resultado dos componentes que describen un corte. De esta manera, el procedimiento de contracción se puede implementar como el algoritmo de Kruskal en el tiempo.$${\ displaystyle O (| E | \ log | E |)}.

Las opciones de bordes aleatorios en el algoritmo de Karger corresponden a una ejecución del algoritmo de Kruskal en un gráfico con rangos de bordes aleatorios hasta que solo quedan dos componentes.

El mejor uso de implementaciones conocidas. $${\ displaystyle O (| E |)} tiempo y espacio, o $${\ displaystyle O (| E | \ log | E |)} tiempo y $${\ displaystyle O (| V |)}espacio, respectivamente. ^[1]

Probabilidad de éxito del algoritmo de contracción [ editar ]

En una grafica $${\ displaystyle G = (V, E)} con $${\ displaystyle n = | V |} vértices, el algoritmo de contracción devuelve un corte mínimo con una probabilidad polinomialmente pequeña $${\ displaystyle {\ binom {n} {2}} ^ {- 1}}. Cada grafica tiene$${\ displaystyle 2 ^ {n-1} -1}cortes, ^[3] entre los cuales a lo sumo$${\ displaystyle {\ tbinom {n} {2}}}Pueden ser cortes mínimos. Por lo tanto, la probabilidad de éxito de este algoritmo es mucho mejor que la probabilidad de elegir un corte al azar, que es como máximo$${\ displaystyle {\ tbinom {n} {2}} / (2 ^ {n-1} -1)}

Por ejemplo, el gráfico del ciclo en$${\ displaystyle n} vértices tiene exactamente $${\ displaystyle {\ binom {n} {2}}}Cortes mínimos, dados por cada elección de 2 aristas. El procedimiento de contracción encuentra cada uno de estos con la misma probabilidad.

Para establecer el límite de la probabilidad de éxito en general, vamos a $${\ displaystyle C} denota los bordes de un corte mínimo específico de tamaño $${\ displaystyle k}. El algoritmo de contracción devuelve$${\ displaystyle C} si ninguno de los bordes al azar pertenece al cutset de $${\ displaystyle C}. En particular, la primera contracción del borde evita$${\ displaystyle C}, lo que pasa con probabilidad $${\ displaystyle 1-k / | E |}. El grado mínimo de$${\ displaystyle G} Por lo menos $${\ displaystyle k} (De lo contrario, un vértice de grado mínimo induciría un corte más pequeño), por lo que $${\ displaystyle | E | \ geq nk / 2}. Por lo tanto, la probabilidad de que el algoritmo de contracción elija un borde de$${\ displaystyle C} es

$${\ displaystyle {\ frac {k} {| E |}} \ leq {\ frac {k} {nk / 2}} = {\ frac {2} {n}}.

La probabilidad $${\ displaystyle p_ {n}} que el algoritmo de contracción en una $${\ displaystyle n}El gráfico de vértices evita $${\ displaystyle C} satisface la recurrencia $${\ displaystyle p_ {n} \ geq \ left (1 - {\ frac {2} {n}} \ right) p_ {n-1}}, con $${\ displaystyle p_ {2} = 1}, que se puede ampliar como

$${\ displaystyle p_ {n} \ geq \ prod _ {i = 0} ^ {n-3} {\ Bigl (} 1 - {\ frac {2} {ni}} {\ Bigr)} = \ prod _ { i = 0} ^ {n-3} {\ frac {ni-2} {ni}} = {\ frac {n-2} {n}} \ cdot {\ frac {n-3} {n-1} } \ cdot {\ frac {n-4} {n-2}} \ cdots {\ frac {3} {5}} \ cdot {\ frac {2} {4}} \ cdot {\ frac {1} { 3}} = {\ binom {n} {2}} ^ {- 1} \ ,.}

Repitiendo el algoritmo de contracción [ editar ]

10 repeticiones del procedimiento de contracción. La quinta repetición encuentra el corte mínimo de tamaño 3.

Repitiendo el algoritmo de contracción. $${\ displaystyle T = {\ binom {n} {2}} \ ln n} veces con opciones aleatorias independientes y devolviendo el corte más pequeño, la probabilidad de no encontrar un corte mínimo es

$${\ displaystyle \ left [1 - {\ binom {n} {2}} ^ {- 1} \ right] ^ {T} \ leq {\ frac {1} {e ^ {\ ln n}}} = { \ frac {1} {n}} \ ,.}

El tiempo total de ejecución para $${\ displaystyle T} repeticiones para una gráfica con $${\ displaystyle n}vértices y $${\ displaystyle m} bordes es $${\ displaystyle O (Tm) = O (n ^ {2} m \ log n)}.

Algoritmo de Karger-Stein [ editar ]

Una extensión del algoritmo de Karger debido a David Karger y Clifford Stein logra una mejora de un orden de magnitud. ^[4]

La idea básica es realizar el procedimiento de contracción hasta que el gráfico alcance $${\ displaystyle t} vértices.

   contrato de trámite ($${\ displaystyle G = (V, E)}
  
, $${\ displaystyle t}
  
):
    mientras {\ displaystyle | V |> t}
  

       escoger $${\ displaystyle e \ en E}
  
 uniformemente al azar
       $${\ displaystyle G \ leftarrow G / e}
  

   regreso $${\ displaystyle G}
  

La probabilidad $${\ displaystyle p_ {n, t}} Que este procedimiento de contracción evita un corte específico. $${\ displaystyle C} en una $${\ displaystyle n}-vertex gráfico es

$${\ displaystyle p_ {n, t} \ geq \ prod _ {i = 0} ^ {nt-1} {\ Bigl (} 1 - {\ frac {2} {ni}} {\ Bigr)} = {\ binom {t} {2}} {\ Bigg /} {\ binom {n} {2}} \ ,.}

Esta expresión es de aproximadamente $${\ displaystyle t ^ {2} / n ^ {2}} y se vuelve menos que $${\ displaystyle {\ frac {1} {2}}} alrededor $${\ displaystyle t = n / {\ sqrt {2}}}. En particular, la probabilidad de que un borde de$${\ displaystyle C}Se contrae crece hacia el final. Esto motiva la idea de cambiar a un algoritmo más lento después de un cierto número de pasos de contracción.

   procedimiento fastmincut ($${\ displaystyle G = (V, E)}
  
):
    si $${\ displaystyle | V | \ leq 6}
  
:
        devolver mincut ($${\ displaystyle V}
  
)
    Otra cosa :
       $${\ displaystyle t \ leftarrow \ lceil 1+ | V | / {\ sqrt {2}} \ rceil}
  

       $${\ displaystyle G_ {1} \ leftarrow}
  
 contrato($${\ displaystyle G}
  
, $${\ displaystyle t}
  
)
       $${\ displaystyle G_ {2} \ leftarrow}
  
 contrato($${\ displaystyle G}
  
, $${\ displaystyle t}
  
)
        return min {fastmincut ($${\ displaystyle G_ {1}}
  
), fastmincut ($${\ displaystyle G_ {2}}
  
)}

Análisis [ editar ]

La probabilidad $${\ displaystyle P (n)} El algoritmo encuentra un cutset específico. $${\ displaystyle C} Está dada por la relación de recurrencia.

$${\ displaystyle P (n) = 1- \ left (1 - {\ frac {1} {2}} P \ left ({\ Bigl \ lceil} 1 + {\ frac {n} {\ sqrt {2}} } {\ Bigr \ rceil} \ right) \ right) ^ {2}}

con solucion $${\ displaystyle P (n) = \ Omega \ left ({\ frac {1} {\ log n}} \ right)}. El tiempo de ejecución de fastmincut satisface

$${\ displaystyle T (n) = 2T \ left ({\ Bigl \ lceil} 1 + {\ frac {n} {\ sqrt {2}}} {\ Bigr \ rceil} \ right) + O (n ^ {2 })}

con solucion $${\ displaystyle T (n) = O (n ^ {2} \ log n)}. Para lograr la probabilidad de error$${\ displaystyle O (1 / n)}, el algoritmo se puede repetir $${\ displaystyle O (\ log n / P (n))} tiempos, para un tiempo total de ejecución de $${\ displaystyle T (n) \ cdot {\ frac {\ log n} {P (n)}} = O (n ^ {2} \ log ^ {3} n)}. Esto es una mejora de un orden de magnitud sobre el algoritmo original de Karger.

Encontrando todos los min-cortes [ editar ]

Teorema: con alta probabilidad podemos encontrar todos los cortes mínimos en el tiempo de ejecución de$${\ displaystyle O (n ^ {2} \ ln ^ {3} n)}.

Prueba: sabemos que$${\ displaystyle P (n) = O \ left ({\ frac {1} {\ ln n}} \ right)}Por lo tanto, después de ejecutar este algoritmo. $${\ displaystyle O (\ ln ^ {2} n)} veces la probabilidad de perder un corte mínimo específico es

$${\ displaystyle \ Pr [{\ text {falta un corte mínimo}}] = (1-P (n)) ^ {O (\ ln ^ {2} n)} \ leq \ left (1 - {\ frac {c} {\ ln n}} \ right) ^ {\ frac {3 \ ln ^ {2} n} {c}} \ leq e ^ {- 3 \ ln n} = {\ frac {1} { n ^ {3}}}}.

Y hay a lo sumo $${\ displaystyle {\ binom {n} {2}}} Los cortes mínimos, por lo tanto, la probabilidad de perder cualquier corte mínimo es

$${\ displaystyle \ Pr [{\ text {perder cualquier corte mínimo}}] \ leq {\ binom {n} {2}} \ cdot {\ frac {1} {n ^ {3}}} = O \ left ({\ frac {1} {n}} \ derecha).}

La probabilidad de fallos es considerablemente pequeña cuando n es lo suficientemente grande.

Límite de mejora [ editar ]

Para determinar un corte mínimo, uno tiene que tocar todos los bordes del gráfico al menos una vez, lo cual es $${\ displaystyle \ Theta (n ^ {2})}Tiempo en una gráfica densa . El algoritmo de corte mínimo de Karger-Stein toma el tiempo de ejecución de$${\ displaystyle O (n ^ {2} \ ln ^ {O (1)} n)}, que está muy cerca de eso.

 algoritmo push-reetiquetado (alternativamente, el algoritmo preflow-push ) es un algoritmo para calcular flujos máximos . El nombre "push-reetiquetado" proviene de las dos operaciones básicas utilizadas en el algoritmo. A lo largo de su ejecución, el algoritmo mantiene un "preflujo" y lo convierte gradualmente en un flujo máximo moviendo el flujo localmente entre nodos vecinos utilizando operaciones de empuje bajo la guía de una red admisible mantenida por operaciones de etiquetado . En comparación, el algoritmo Ford-Fulkerson realiza aumentos globales que envían flujos siguiendo las rutas desde la fuente hasta el sumidero. ^[1]

El algoritmo push-reetiqueta se considera uno de los algoritmos de flujo máximo más eficientes. El algoritmo genérico tiene una complejidad de tiempo O ( V  ² E ) fuertemente polinómica , que es asintóticamente más eficiente que el algoritmo Edmonds-Karp O ( VE  ² ) . ^[2] Las variantes específicas de los algoritmos logran complejidades de tiempo aún más bajas. La variante basada en la regla de selección de nodo de etiqueta más alta tiene una complejidad de tiempo O ( V  ² √ E ) y generalmente se considera como el punto de referencia para los algoritmos de flujo máximo. ^[3] [4] La complejidad del tiempo de la subcubic O ( registro de VE ( V  ² / E )) se puede lograr utilizando árboles dinámicos , aunque en la práctica es menos eficiente. ^[2]

El algoritmo push-reetiquetado se ha ampliado para calcular los flujos de costos mínimos . ^[5] La idea de las etiquetas de distancia ha llevado a un algoritmo de ruta de aumento más eficiente, que a su vez puede incorporarse nuevamente al algoritmo push-reetiquetado para crear una variante con un rendimiento empírico aún mayor.

Historia [ editar ]

El concepto de preflujo fue diseñado originalmente por Alexander V. Karzanov y se publicó en 1974 en Soviet Mathematical Dokladi 15. Este algoritmo de flujo previo también usaba una operación de empuje; sin embargo, usó distancias en la red auxiliar para determinar dónde empujar el flujo en lugar de un sistema de etiquetado. ^[2] [7]

El algoritmo push-relabel fue diseñado por Andrew V. Goldberg y Robert Tarjan . El algoritmo se presentó inicialmente en noviembre de 1986 en STOC '86: Actas del decimoctavo simposio anual de la ACM sobre Teoría de la computación, y luego oficialmente en octubre de 1988 como un artículo en el Journal of the ACM. Ambos documentos detallan una forma genérica del algoritmo que termina en O ( V  ² E ) junto con una implementación secuencial O ( V  ³ ) , una O ( registro de VE ( V  ² / E ))Implementación utilizando árboles dinámicos, e implementación paralela / distribuida. ^[2] [8] . Una explicación en ^[9] Goldberg-Tarjan introdujo las etiquetas de distancia incorporándolas en el algoritmo de flujo máximo paralelo de Yossi Shiloach y Uzi Vishkin ^[10] .

Conceptos [ editar ]

Definiciones y notaciones [ editar ]

Artículo principal: Red de flujo

Dejar:

• G = ( V , E ) sea ​​una red con función de capacidad c : V × V → ℝ _∞ ,
• F = ( G , c , s , t ) una red de flujo , donde s ∈ V y t ∈ V son losvértices fuente y sumideroelegidosrespectivamente,
• f  : V × V → ℝ denota un flujo previo en F ,
• x _f  : V → ℝ denota lafunción de exceso con respecto al flujo f , definido porx _f ( u ) = ∑ _v ∈ V f ( v , u ) - ∑ _v ∈ V f ( u , v ) ,
• c _f  : V × V → ℝ _∞ denota la función de capacidad residual con respecto al flujo f , definido porc _f  ( e ) = c ( e ) - f  ( e ) ,

y

• G _f ( V , E _f  ) denota la red residual de G con respecto al flujo f .

El algoritmo push-reetiquetado utiliza una función de etiquetado válido de entero no negativo que utiliza etiquetas de distancia , o alturas , en nodos para determinar qué arcos deben seleccionarse para la operación push. Esta función de etiquetado se denota por 𝓁: V → ℕ . Esta función debe cumplir las siguientes condiciones para ser considerada válida:

Etiquetado válido :

𝓁 ( u ) ≤ 𝓁 ( v ) + 1 para todos ( u , v ) ∈ E _f

Condición de la fuente :

𝓁 ( s ) = | V  |

Conservación del sumidero :

𝓁 ( t ) = 0

En el algoritmo, los valores de etiqueta de s y t son fijos. 𝓁 ( u ) es un límite inferior de la distancia no ponderada de u a t en G _f   si t es accesible desde u . Si u ha sido desconectado de t , entonces 𝓁 ( u ) - | V  | es un límite inferior de la distancia no ponderada de u a s . Como resultado, si existe una función de etiquetado válida, no hay rutas s - t en G_f   porque no hay caminos que puedan ser más largos que| V  | - 1.

Un arco ( u , v ) ∈ E _f   se llama admisible si 𝓁 ( u ) = 𝓁 ( v ) + 1 . La red admisible G _f ( V , E _f  ) se compone del conjunto de arcos e ∈ E _f   que son admisibles. La red admisible es acíclica.

Operaciones [ editar ]

Inicialización [ editar ]

El algoritmo comienza creando un gráfico residual, inicializando los valores de preflujo a cero y realizando un conjunto de operaciones de saturación de empuje en arcos residuales que salen de la fuente, ( s , v ) donde v ∈ V \ { s } . De manera similar, las etiquetas se inicializan de tal manera que la etiqueta en la fuente es el número de nodos en el gráfico, 𝓁 ( s ) = | V  | , y todos los demás nodos reciben una etiqueta de cero. Una vez que se completa la inicialización, el algoritmo realiza repetidamente las operaciones de inserción o de reetiquetado contra los nodos activos hasta que no se pueda realizar ninguna operación aplicable.

Pulse [ editar ]

La operación de inserción se aplica en un arco de salida admisible ( u , v ) de un nodo activo u en G _f . Mueve las unidades de flujo mín { x _f ( u ), c _f ( u , v )} de u a v .

empujar (u, v):
    afirmar x f [u]> 0 y 𝓁 [u] == 𝓁 [v] + 1
    Δ = min (x f [u], c [u] [v] - f [u] [v])
    f [u] [v] + = Δ
    f [v] [u] - = Δ
    x f [u] - = Δ
    x f [v] + = Δ

Una operación de empuje que hace que f  ( u , v ) alcance a c ( u , v ) se denomina empuje de saturación, ya que consume toda la capacidad disponible del arco residual. De lo contrario, todo el exceso en el nodo se empuja a través del arco residual. Esto se llama un empuje insaturante o no saturante .

Reetiquetar [ editar ]

La operación de reetiquetado se aplica en un nodo activo u sin ningún tipo de arcos admisibles en G _f . Modifica 𝓁 ( u ) para que sea el valor mínimo, de manera que se cree un arco exterior admisible. Tenga en cuenta que esto siempre aumenta 𝓁 ( u ) y nunca crea un arco pronunciado, que es un arco ( u , v ) tal que c _f  ( u , v )> 0 , y 𝓁 ( u )> 𝓁 ( v ) + 1 .

reetiquetar (u):
    afirmar x f [u]> 0 y 𝓁 [u] <= 𝓁 [v] para todos v tales que c [u] [v] - f [u] [v]> 0
    𝓁 [u] = min (𝓁 [v] para todo v tal que c [u] [v] - f [u] [v]> 0) + 1

Efectos de empuje y reetiquetar [ editar ]

Después de una operación de empujar o volver a etiquetar, 𝓁 sigue siendo una función de etiquetado válida con respecto a f .

Para una operación de empuje en un arco admisible ( u , v ) , puede agregar un arco ( v , u ) a E _f , donde 𝓁 ( v ) = 𝓁 ( u ) - 1 ≤ 𝓁 ( u ) + 1 ; también puede eliminar el arco ( u , v ) de E _f , donde elimina efectivamente la restricción 𝓁 ( u ) ≤ 𝓁 ( v ) + 1 .

Para ver que una operación de reetiquetado en el nodo u conserva la validez de 𝓁 ( u ) , observe que esto está garantizado trivialmente por definición para los arcos de salida de u en G _f . Para los in-arcos de u en G _f , el aumento de 𝓁 ( u ) solo puede satisfacer las restricciones con menos fuerza, no violarlas.

El algoritmo genérico push-reetiquetar [ editar ]

El algoritmo genérico push-reetiquetado se usa solo como prueba de concepto y no contiene detalles de implementación sobre cómo seleccionar un nodo activo para las operaciones push y reetiquetado. Esta versión genérica del algoritmo terminará en O ( V ² E ) .

Desde 𝓁 ( s ) = | V  | , 𝓁 ( t ) = 0 , y no hay rutas más largas que | V  | - 1 en G _f , con el fin de 𝓁 ( s ) para satisfacer la condición válida etiquetado s debe estar desconectado de t . En la inicialización, el algoritmo cumple este requisito al crear un flujo previo f que satura todos los arcos de salida de s , después de lo cual 𝓁 ( v ) = 0es trivialmente válido para todos v ∈ V \ { s, t } . Después de la inicialización, el algoritmo ejecuta repetidamente una operación de inserción o reetiquetado aplicable hasta que no se apliquen tales operaciones, momento en el que el flujo previo se ha convertido en un flujo máximo.

genérico-push-reetiquetar (G, c, s, t):
    cree un flujo previo f que sature todos los arcos de salida de s
    vamos a 𝓁 [s] = | V |
    vamos a 𝓁 [v] = 0 para todos v ∈ V \ {s}
    Mientras que hay una operación de empuje o reetiquetado aplicable
        ejecutar la operación

Corrección [ editar ]

El algoritmo mantiene la condición de que 𝓁 es un etiquetado válido durante su ejecución. Esto puede comprobarse si se examinan los efectos de las operaciones de inserción y etiquetado en la función de etiqueta . La operación de reetiquetado aumenta el valor de la etiqueta en el mínimo asociado más uno que siempre cumplirá con la restricción 𝓁 ( u ) ≤ 𝓁 ( v ) + 1 . La operación de empuje puede enviar el flujo de u a v si ( u ) = 𝓁 ( v ) + 1 . Esto puede agregar ( v , u ) a G _f  y puede eliminar (u , v ) de G _f  . La adición de ( v , u ) aG _f  no afectará el etiquetado válido ya que 𝓁 ( v ) = 𝓁 ( u ) - 1 . La eliminación de ( u , v ) de G _f  elimina la restricción correspondiente, ya que la propiedad de etiquetado válida 𝓁 ( u ) ≤ 𝓁 ( v ) + 1 solo se aplica a los arcos residuales en G _f  . ^[8]

Si existe un preflujo fy un etiquetado válido 𝓁 para f , entonces no hay un camino de aumento de s a t en el gráfico residual G _f  . Esto puede comprobarse mediante una contradicción basada en las desigualdades que surgen en la función de etiquetado cuando se supone que existe un camino de aumento. Si el algoritmo termina, entonces todos los nodos en V \ { s , t } no están activos. Esto significa que todos los v ∈ V \ { s , t } no tienen exceso de flujo, y sin exceso el preflujo fobedece a la restricción de conservación del flujo y puede considerarse un flujo normal. Este flujo es el flujo máximo de acuerdo con el teorema de corte mínimo de flujo máximo, ya que no hay una ruta de aumento desde s hasta t . ^[8]

Por lo tanto, el algoritmo devolverá el flujo máximo al terminar.

Complejidad temporal [ editar ]

Para limitar la complejidad del tiempo del algoritmo, debemos analizar el número de operaciones de inserción y de reetiquetado que ocurren dentro del bucle principal. Los números de reetiquetado, saturación de empuje y no saturación de las operaciones de empuje se analizan por separado.

En el algoritmo, la operación de reetiquetado se puede realizar a lo sumo (2 |  V  | - 1) (|  V  | - 2) <2 font="" nbsp="">V  | ²veces Esto se debe a que el valor de etiquetado 𝓁 ( u ) para cualquier nodo u nunca puede disminuir, y el valor máximo de la etiqueta es a lo sumo 2 | V  | - 1 para todos los nodos. Esto significa que la operación de reetiquetado podría realizarse potencialmente 2 | V  | - 1 vez para todos los nodos V \ { s , t } (es decir, |  V  | - 2). Esto resulta en un límite deO ( V  ² ) para la operación de reetiquetado.

Cada pulsación de saturación en un arco admisible ( u , v ) elimina el arco de G _f  . Para que el arco se vuelva a insertar en G _f  para otro empuje de saturación, v primero debe volver a etiquetarse, seguido de un empuje en el arco ( v , u ) , y luego se debe volver a etiquetar u . En el proceso, 𝓁 ( u ) aumenta en al menos dos. Por lo tanto, hay pulsaciones de saturación de O ( V ) en ( u , v ), y el número total de empujes de saturación es como máximo 2 | V  || E  | . Esto da como resultado un límite de tiempo de O ( VE ) para las operaciones de empuje de saturación.

El límite del número de empujes no saturantes se puede lograr a través de un argumento potencial . Utilizamos la función potencial Φ = ∑ _{[ u ∈ V ∧ x f  ( u )> 0]} 𝓁 ( u ) (es decir, Φ es la suma de las etiquetas de todos los nodos activos). Es obvio que Φ es 0 inicialmente y permanece no negativo durante la ejecución del algoritmo. Ambos etiqueta de nuevo y empuja saturando pueden aumentar Φ . Sin embargo, el valor de Φdebe ser igual a 0 en la terminación ya que no puede haber ningún nodo activo al final de la ejecución del algoritmo. Esto significa que durante la ejecución del algoritmo, los empujes no saturantes deben compensar la diferencia de las operaciones de etiquetado y saturación para que Φ termine con un valor de 0.

La operación de reetiquetado puede aumentar Φ como máximo (2 |  V  | - 1) (|  V  | - 2) . Una pulsación de saturación en ( u , v ) activa v si estaba inactiva antes de la pulsación, aumentando Φ como máximo 2 | V  | - 1 . Por lo tanto, la contribución total de todas las operaciones de saturación de empuje a Φ es como máximo (2 |  V  | - 1) (2 |  V  ||  E  |) . Un impulso no saturante ( u , v ) siempre se desactiva.u , pero también puede activar v como en un impulso de saturación. Como resultado, disminuye Φ al menos 𝓁 ( u ) - 𝓁 ( v ) = 1 . Desde etiqueta de nuevo y empuja saturando aumentan Φ , el número total de pulsaciones nonsaturating debe compensar la diferencia de (2 |  V  | - 1) (|  V  | - 2) + (2 |  V  | - 1) (2 |  V  ||  E  |) ≤ 4 | V  | ² | E  | . Esto resulta en un límite de tiempo de O ( V  ² E ) Para las operaciones de empuje no saturantes.

En resumen, el algoritmo ejecuta las reclasificaciones O ( V  ² ) , las pulsaciones de saturación O ( VE ) y las pulsaciones no saturantes O ( V  ² E ) . Las estructuras de datos se pueden diseñar para seleccionar y ejecutar una operación aplicable en O (1) tiempo. Por lo tanto, la complejidad del tiempo del algoritmo es O ( V  ² E ) . ^[1] [8]

Ejemplo [ editar ]

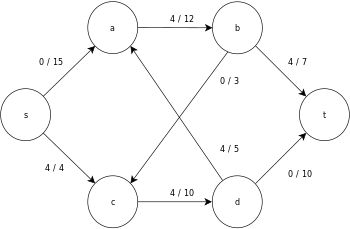
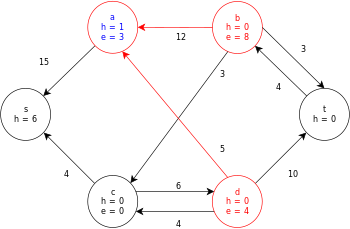
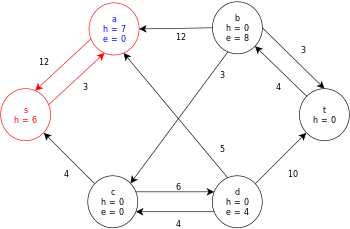
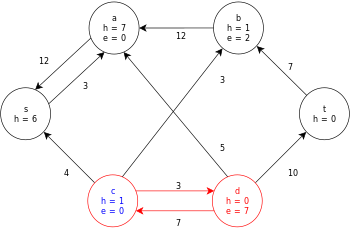
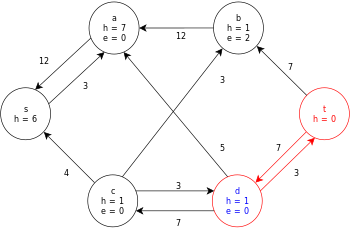
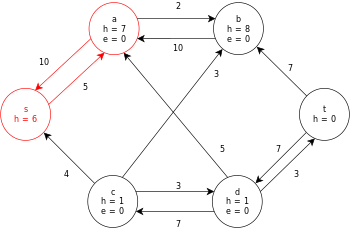
La siguiente es una ejecución de muestra del algoritmo genérico de cambio de marca, como se definió anteriormente, en el siguiente diagrama de flujo de red simple.

Gráfico de red de flujo inicial

Gráfico de red de flujo máximo final

En el ejemplo, los valores h y e denotan la etiqueta 𝓁 y el exceso x _f  , respectivamente, del nodo durante la ejecución del algoritmo. Cada gráfico residual en el ejemplo solo contiene los arcos residuales con una capacidad mayor que cero. Cada gráfico residual puede contener múltiples iteraciones del bucle de operación de ejecución .

Operación (s) de algoritmo	Grafica residual
Inicialice el gráfico residual estableciendo el preflujo en los valores 0 e inicializando el etiquetado.
El empuje inicial de saturación se realiza en todos los arcos de preflujo fuera de la fuente, s .
El nodo a se vuelve a etiquetar para empujar su exceso de flujo hacia el fregadero, t . El exceso en a se empuja entonces a b, luego d en dos empujes de saturación subsiguientes; Lo que todavía deja un poco de exceso.
Una vez más, a se vuelve a etiquetar para empujar su exceso a lo largo de su último residuo positivo restante (es decir, empujar el exceso de nuevo a s ). El nodo a se elimina del conjunto de nodos activos.
Vuelva a etiquetar b y luego empuje su exceso haciat y c .
Vuelva a etiquetar c y luego empuje su exceso haciad .
Vuelva a etiquetar d y luego empuje su exceso a t .
Esto deja al nodo b como el único nodo activo restante, pero no puede empujar su exceso de flujo hacia el sumidero. Vuelva a etiquetar b y luego empuje su exceso hacia la fuente, s , a través del nodo a .
Empuje el último bit de exceso en una vuelta a la fuente, s . No quedan nodos activos. El algoritmo finaliza y devuelve el flujo máximo del gráfico (como se ve arriba).

El ejemplo (pero con un flujo inicial de 0) se puede ejecutar aquí de forma interactiva.