INSTRUMENTOS DE MEDICIÓN

groma o gruma (por deformación, quizá vía el etrusco, de la palabra griega gnomon ( γνὠμων) que significaba “escuadra”) era el aparato de nivelación esencial de los agrimensores de la antigua Roma.

Descripción[editar]

Consistía en una pértiga vertical que soportaba a su extremidad superior un travesaño situado sobre un pivote: el travesaño podía así girar en el plano horizontal. Cada brazo del travesaño soportaba en su extremidad una plomada.

La groma servía para comprobar las alineaciones y la corrección de las direcciones perpendiculares. Por abuso del lenguaje, este término vino a designar el centro de un campamento militar romano o el foro en la fundación de una ciudad, o la intersección del cardo y del decumanus , ya que el ángulo recto formado por las direcciones de estas dos arterias, era comprobado con la groma por los agrimensores.

Arqueólogos e historiadores han discutido durante largo tiempo sobre los instrumentos topográficos utilizados por los romanos basándose en el hallazgo de varios trozos de metal en las ruinas de la antigua Pompeya y otras zonas del Imperio Romano.
En una excavación en Bavaria se encontró una cruz de hierro perforada por el centro en cuyos extremos había restos de unos ganchos de hierro: era la groma romana. Actualmente se sabe que la groma era el instrumento topográfico más utilizado por los romanos.
El diseño y el principio de la groma es simple: Consistía en 2 brazos (de aproximadamente 1 m. de longitud) cruzados perpendicularmente. Estos brazos iban atados a una tabla que se balanceaba fijada a un cuerpo de madera, compensando así la groma para facilitar su empleo. Junto al pie del operario estaba el ferramentum, un “pie de hierro ” que tenía cuatro grandes alas para dotarla de estabilidad, y una punta aguda al final para clavarla en el suelo si era necesario. Del final de cada uno de los cuatro extremos colgaba una cuerda con o sin plomada. Había una quinta plomada que iba atada al umbilicus soli (el centro de la cruz) y servía para situar el instrumento sobre el punto base para la medición.
La groma se utilizaba para observar y establecer líneas directas y Ángulos rectos. El topógrafo observaba la diagonal a través de un par de cuerdas para proyectar rectas o trazar líneas perpendiculares a la línea definida por el par de plomadas, trabajando solo en el plano horizontal sin considerar las diferencias de cota.
Este sencillo instrumento servía para establecer alineaciones de caminos, creando calles para ciudades y campos militares, y sobre todo, para parcelar determinadas extensiones de terreno. Su punto débil era el viento que desviaba las plomadas y hacia muy difícil el trabajo durante días tempestuosos.

hipsómetro (del gr. ὕψος, altitud y μέτρον, medida) es un instrumento de medición utilizado para determinar la altitud sobre el nivel del mar de un lugar a partir de la temperatura de ebullición de un líquido.¹​ Por extensión, también se denominan hipsómetros a un tipo de instrumentos con los que puede obtenerse la elevación de un punto sobre un nivel de referencia basándose en métodos de medición directa (mediante trigonometría).

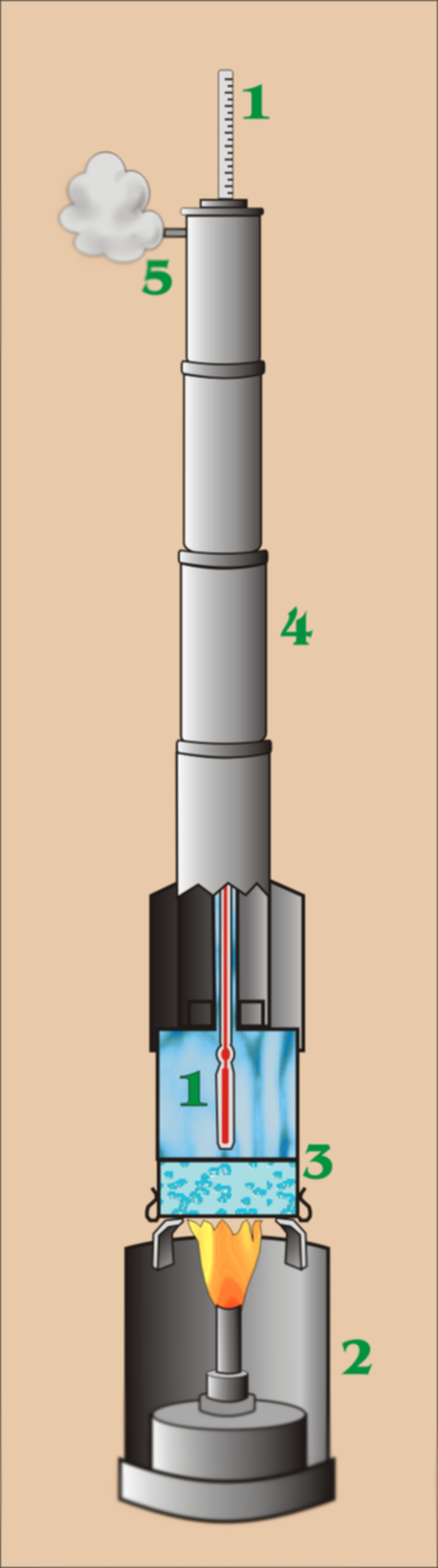
El hipsómetro de presión, como se muestra en el dibujo de la derecha, emplea el principio de que el punto de ebullición de un líquido disminuye al disminuir la presión atmosférica, y que la presión barométrica a su vez se reduce con la altura del punto de observación.

El instrumento consiste en un recipiente cilíndrico en el que un líquido, habitualmente agua, se hierve. Por la camisa exterior circula el vapor, mientras que en el compartimento central se coloca un termómetro. Para deducir la altura sobre el nivel del mar del punto observado, es necesario conocer la relación existente entre el punto de ebullición y la presión, y también entre la presión y la altura barométrica.

Un dispositivo basado en la reducción del punto de ebullición del agua fue ideado por el científico colombiano Francisco José de Caldas.²​ Su hipsómetro utiliza la dependencia existente entre el punto de ebullición de los líquidos y la presión atmosférica. A medida que aumenta la altitud, disminuye la temperatura necesaria para que el agua alcance el punto de ebullición. En 1817, un año después de la muerte del Sabio Caldas, William Hyde Wollastonpresentó un hipsómetro mejorado en el que el termómetro dejaba de encontrarse inmerso en agua y pasaba a estar expuesto únicamente a su vapor.

En 1845, Henri Victor Regnault presentó el hipsómetro transportable, de dimensiones reducidas.³​

Hipsómetro de escala[editar]

Es conocido desde la Grecia clásica que es posible medir por semejanza de triángulos la altura de un objeto sin necesidad de acceder hasta su punto más alto si se puede medir su sombra.⁴​ Un simple hipsómetro de escala permite calcular la altura de un edificio o un árbol leyendo la medida de una plomada sobre una regla con la que se apunta a la parte superior de un objeto cuando se conoce la distancia desde el objeto hasta el observador. Los hipsómetros modernos usan una combinación de telémetro láser y clinómetro para medir distancias a la parte superior e inferior de los objetos y el ángulo entre las líneas desde el observador hasta cada uno de estos dos puntos para calcular la altura.

Aquí se ilustra un ejemplo de un hipsómetro de escala. Consiste en una mira de observación, una escala horizontal fija y una escala vertical ajustable con una línea de plomada adjunta. El principio de funcionamiento de un hipsómetro de escala se basa en la idea geométrica de los triángulos semejantes.

En primer lugar, se sitúa la escala vertical ajustable a una distancia adecuada, para que la lectura de la plomada quede dentro de la regla. A continuación, como en el paso 1 de la ilustración, se toma una visual dirigida a la parte superior del objeto cuya altura debe determinarse, y se registra la lectura en la escala horizontal h' (según se indica en la figura (c)). El cálculo a partir de este valor dará finalmente la altura h comprendida entre la línea horizontal desde el ojo del observador hasta la parte superior del objeto cuya altura se quiere determinar. Del mismo modo, como en el paso 2 de la ilustración, se realiza una observación sobre la base del objeto cuya altura quiere determinarse, y se registra la lectura en la escala horizontal d' (según se indica en la figura (f)). El cálculo de este valor dará la distancia desde la base del objeto a la línea horizontal donde se sitúa el ojo del observador. Finalmente, se debe medir la distancia x del observador al objeto.

Al observar la geometría involucrada en el paso 1, se obtiene el esquema (a): dos triángulos en ángulo recto, que se muestran aquí con los mismos ángulos pequeños en color amarillo. A continuación, en el esquema (b) se observa que los dos triángulos tienen ángulos idénticos: cada uno tiene un ángulo recto, el mismo ángulo pequeño marcado en amarillo y el mismo ángulo grande marcado en naranja. Por lo tanto, en el esquema (c) se observa que al usar el principio de los triángulos semejantes, dado que los dos triángulos tienen ángulos idénticos, los lados estarán en proporción: la distancia al objeto x es proporcional a x' , la altura establecida en la escala vertical del hipsómetro; y la altura h del objeto por encima de la línea del ojo de los observadores es proporcional a h' , la lectura de la escala horizontal del hipsómetro.

Dado que:

tangente (ángulo pequeño amarillo) = lado opuesto / lado adyacente

entonces

tangente (ángulo pequeño amarillo) = h / x = h' / x'

y por lo tanto

h = h' x / x'

Del mismo modo, la geometría involucrada en el paso 2 da como resultado el esquema (d): dos triángulos rectángulos. A continuación, en el esquema se observa que los dos triángulos tienen ángulos idénticos: cada uno tiene un ángulo recto, el mismo ángulo pequeño se muestra en amarillo y el mismo ángulo grande se muestra en naranja. Por lo tanto, en el esquema (f) se aprecia que al usar de nuevo el principio de los triángulos semejantes, dado que los dos triángulos tienen ángulos idénticos, los lados estarán en proporción: la distancia x al objeto es proporcional a x' , la altura establecida en la escala vertical del hipsómetro; y la profundidad d de la visual del objeto por debajo de la línea horizontal es proporcional a d' , la lectura de la escala horizontal del hipsómetro.

Dado que:

tangente (ángulo pequeño) = lado opuesto / lado adyacente

entonces

tangente (ángulo pequeño) = d / x = d' / x'

y por lo tanto

d = d' x / x'

En consecuencia, la altura total del objeto es:

h + d = (h' + d' ) x / x'