CONCEPTOS FÍSICOS

CONCEPTOS FUNDAMENTALES

posición de una partícula indica su localización en el espacio o en el espacio-tiempo. Se representa mediante sistemas de coordenadas.

En mecánica clásica, la posición de una partícula en el espacio se representa como una magnitud vectorial respecto a un sistema de coordenadas de referencia. En relatividad general, la posición no es representable mediante un vector euclidiano, ya que en el espacio-tiempo es curvo en esa teoría, por lo que la posición necesariamente debe representarse mediante un conjunto de coordenadas curvilíneas arbitrarias, que en general no pueden ser interpretadas como las componentes de un vector físico genuino. En mecánica cuántica, la representación de la posición de una partícula es aún más compleja, debido a los efectos de no localidad relacionados con el problema de la medida de la mecánica cuántica.

En general, en un sistema físico o de otro tipo, se utiliza el término posición para referirse al estado físico o situación distinguible que exhibe el sistema. Así es común hablar de la posición del sistema en un diagrama que ilustre variables de estado del sistema.

Posición de un punto P en un sistema de coordenadas cartesianas.

Vector posición en mecánica clásica[editar]

En mecánica clásica, debido al carácter euclídeo del espacio, la posición de una partícula se representa mediante el vector de posición o radio vector, usualmente simbolizado con la letra ${\displaystyle \mathbf {r} }$ o mediante las coordenadas del punto geométrico del espacio en el que se encuentra la partícula.

La diferencia del vector posición entre dos posiciones distintas recibe el nombre de vector desplazamiento y se le designa por ${\displaystyle \Delta \mathbf {r} \,}$ (desplazamiento finito) o por ${\displaystyle d\mathbf {r} \,}$ (desplazamiento infinitesimal).

Sistemas de referencia[editar]

Vector de posición de una partícula en el sistema de coordenadas cartesianas.

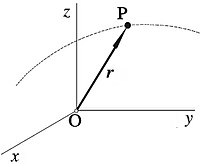
Podemos representar la posición de una partícula o de un punto del espacio, respecto de un sistema de ejes, mediante las coordenadas cartesianas (x,y,z) del punto, o mediante el vector de posición de dicho punto respecto al origen "O" del sistema de coordenadas (Figura 1). Dicho vector de posición se define como el vector que tiene como origen el punto "O" y como extremo el punto "P", es decir, el vector aplicado en el punto "O" que tiene como componentes las coordenadas cartesianas x, y, z, del punto "P". Escribiremos

${\displaystyle \mathbf {r} ={\mbox{OP}}=x\mathbf {i} +y\mathbf {j} +z\mathbf {k} \,}$

siendo ${\displaystyle \mathbf {i} ,\mathbf {j} ,\mathbf {k} \,}$ los versores asociados a los ejes coordenados respectivos. En general, un sistema de referencia queda definido por un origen y una base vectorial asociada. Si la base vectorial es ortogonal (i.e., si los tres versores que la definen son perpendiculares entre sí), el sistema de referencia también es ortogonal.

Traslación y rotación del sistema de referencia[editar]

Vectores de posición de una partícula en dos sistema de coordenadas cartesianas paralelos entre sí pero con distinto origen.

Componentes del vector de posición de una partícula en dos sistema de coordenadas cartesianas con distinto origen rotados entre sí.

Merece particular atención considerar el vector de posición cuando cambia por traslación el sistema de referencia, pues entonces cambia el vector de posición del punto P. Entre los vectores de posición del punto P respecto a los sistemas de referencia de origen en O y en O′ existe la relación

${\displaystyle \mathbf {r} ={\mbox{OO}}'+\mathbf {r} '\,}$

y, consecuentemente, las componentes del vector de posición no son invariantes en las traslaciones del sistema de referencia.

De mismo modo, las componentes del vector de posición no son invariantes en las rotaciones del sistema de referencia, transformando sus componentes mediante la correspondiente matriz de rotación.

Derivada temporal del vector de posición[editar]

Cuando la partícula permanece en reposo en el sistema de referencia, sus coordenadas no cambian en el transcurso del tiempo y su vector de posición será constante:

${\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k} }$

Si la posición de una partícula puntual P cambia con el tiempo, en un instante dado se representa por:

${\displaystyle \mathbf {r} (t)=x(t)\mathbf {i} +y(t)\mathbf {j} +z(t)\mathbf {k} }$

En un sistema de referencia fijo, la base coordenada para expresar la posición de vectores tiene la propiedad de permanecer fija, con lo cual el vector velocidad respecto a un sistema inercial puede obtenerse simplemente derivando las componentes del vector de posición respecto al tiempo:

${\displaystyle \mathbf {v} (t)={\frac {d\mathbf {r} (t)}{dt}}={\frac {dx(t)}{dt}}\mathbf {i} +{\frac {dy(t)}{dt}}\mathbf {j} +{\frac {dz(t)}{dt}}\mathbf {k} }$

Esto contrasta con el caso de un sistema de referencia móvil, en los que aparecen términos adicionales asociados al movimiento del referencial.

Derivada del vector de posición en referenciales en rotación[editar]

Velocidad absoluta y velocidad relativa de una partícula en movimiento con respecto a dos referenciales.

Cuando el movimiento de la partícula se describe a un sistema de referencia móvil (x,y,z) en rotación con respecto de un referencial fijo (X,Y,Z) con el que comparte el mismo origen, el vector de posición será el mismo en ambos referenciales y vendrá expresado por:

${\displaystyle \mathbf {r} (t)=x(t)\mathbf {i} (t)+y(t)\mathbf {j} (t)+z(t)\mathbf {k} (t)}$

en el referencial móvil (x,y,z). Puesto que los versores cartesianos (i,j,k)son función del tiempo, al derivar el vector posición con respecto al tiempo aparecerán términos relacionados se obtiene:

${\displaystyle {\frac {d\mathbf {r} (t)}{dt}}=\left({\frac {dx}{dt}}\mathbf {i} +{\frac {dy}{dt}}\mathbf {j} +{\frac {dz}{dt}}\mathbf {k} \right)+{\boldsymbol {\omega }}\times \mathbf {r} }$

siendo ${\displaystyle {\boldsymbol {\omega }}\,}$ la velocidad angular asociada a la rotación del referencial móvil con respecto al referencial fijo.

En términos de la geometría diferencial los términos adicionales tienen que ver con la conexión asociada al sistema de coordenadas o referencia escogido:

${\displaystyle {\begin{cases}{\cfrac {d\mathbf {i} (t)}{dt}}=\left(\Gamma _{j1}^{1}\mathbf {i} +\Gamma _{j1}^{2}\mathbf {j} +\Gamma _{j1}^{3}\mathbf {k} \right)v^{j}\\\\{\cfrac {d\mathbf {j} (t)}{dt}}=\left(\Gamma _{j2}^{1}\mathbf {i} +\Gamma _{j2}^{2}\mathbf {j} +\Gamma _{j2}^{3}\mathbf {k} \right)v^{j}\\\\{\cfrac {d\mathbf {k} (t)}{dt}}=\left(\Gamma _{j3}^{1}\mathbf {i} +\Gamma _{j3}^{2}\mathbf {j} +\Gamma _{j3}^{3}\mathbf {k} \right)v^{j}\end{cases}}}$

Donde:

${\displaystyle \Gamma _{ij}^{k}\,}$ son los símbolos de Christoffel que caracterizan la conexión.

${\displaystyle v^{j}\,}$ son las componentes de la velocidad.

Posición en mecánica relativista[editar]

En la teoría especial de la relatividad el espacio-tiempo de Minkowski tiene geometría pseudoeuclídea pero en lo esencial existe una biyección entre ese espacio y ${\displaystyle \scriptstyle \mathbb {R} ^{4}}$ por lo que puede definirse un cuadrivector posición análogo en muchos aspectos al vector posición de la mecánica clásica:

${\displaystyle \mathbf {X} =(X^{0},X^{1},X^{2},X^{3})=(ct,x,y,z)\,}$

La derivada de este vector respecto al tiempo propio resulta ser la cuadrivelocidad que es el análogo relativista de la velocidad de la mecánica clásica:

${\displaystyle \mathbf {U} ={\frac {d\mathbf {X} }{d\tau }}=(U^{0},U^{1},U^{2},U^{3})=\gamma (c,v_{x},v_{y},v_{z})\,}$

Sin embargo en la teoría general de la relatividad las cosas se complican debido a que en ese contexto el espacio-tiempo generalmente es curvo. En ese caso no existe una biyección directa entre el espacio-tiempo y el espacio euclídeo tridimensional y por tanto no resulta posible describir la posición de un punto del espacio-tiempo mediante un vector euclídeo. Aunque como el espacio-tiempo cuatridimensional es localmente difeomórfico con el espacio eclídeo tridimensional, pueden emplearse coordenadas curvilíneas que tienen leyes de transformación tensorial similares a un cuadrivector, aunque las cuatro coordenadas de un punto no pueden ser identificadas con un cuadrivector.

Posición en mecánica cuántica[editar]

En mecánica cuántica no-relativista para la mayoría de los sistemas no puede hablarse de la posición de una determinada partícula o incluso de su trayectoria. Esto es una consecuencia del principio de incertidumbre de Heisenberg. En esta teoría las coordenadas intervienen sólo como argumento de la función de onda que describe un sistema, pero en general esas coordenadas no designan la posición de ninguna partícula.

 relación masa carga ( ^m⁄_Q) es una magnitud física usada en la electrodinámica de las partículas cargadas. Como implica su nombre la relación masa carga de un objeto resulta de dividir la masa del objeto entre su carga eléctrica. Esta magnitud generalmente solo es útil cuando el objeto es una partícula. Para objetos macroscópicos la carga total, la densidad de carga, la masa total o la densidad de la masa suelen ser magnitudes más útiles. En el sistema internacional de unidades se mide en kg/C. El concepto (m/Q) aparece en los campos de la microscopía electrónica, espectrometría de masas, tubos de rayos catódicos, física del acelerador, física nuclear, espectroscopia electrónica Auger, cosmología y óptica ionica.¹​ La importancia de la relación carga masa resulta de que, según la electrodinámica clásica, dos partículas con la misma relación masa carga se desplazan con la misma trayectoria en el vacío cuando son sometidas a campos magnéticos.

En algunos campos se usa su inversa la relación carga masa ( ^Q⁄_m). El CODATA recomendó en 2010 un valor para el electrón de  ^e⁄_me= 1,758820088±39×10¹¹ C/kg.

Origen[editar]

Según la física clásica, cuando una partícula cargada se desplaza por campos eléctricos o magnéticos se aplican las dos leyes siguientes:

${\displaystyle \mathbf {F} =Q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}$		(ley de la fuerza de Lorentz)
${\displaystyle \mathbf {F} =m\mathbf {a} =m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}}$		(segunda ley de Newton del movimiento)

Donde F es la fuerza aplicada a la partícula cargada (ion), m es la masa de la partícula, a es la aceleración, Q es la carga eléctrica, E es el campo eléctrico, y v × B es el producto vectorial de la velocidad del ion y la inducción magnética.

Al combinar las dos ecuaciones de campo anteriores surge la ecuación:

${\displaystyle \left({\frac {m}{Q}}\right)\mathbf {a} =\mathbf {E} +\mathbf {v} \times \mathbf {B} }$.

Esta ecuación diferencial es la ecuación clásica para el movimiento de una partícula cargada en el vacío. Junto con las condiciones iniciales de la partícula determina el movimiento de la partícula en el espacio con el tiempo. Tiene como consecuencia que dos partículas con la misma relación m/Q se desplazarán de la misma forma a través del campo.^{nota 1}​Por ello la relación masa carga es una magnitud física importante en los ámbitos científicos donde las partículas cargadas interactúan con campos magnéticos o eléctricos.

Excepciones[editar]

Existen algunos efectos no clásicos derivados de la mecánica cuántica como el efecto Stern–Gerlach que hace que la trayectoria de iones con idéntica m/Q se bifurque.

Símbolos y unidades[editar]

Los símbolos recomendados por la IUPAC para la masa y a carga son m y Q, respectivamente,³​^:4:14 aunque el uso de la minúscula q para la carga también es común. La carga es una magnitud escalar, lo que significa que puede ser tanto positiva (+) como negativa (−). La unidad del SI para la carga es el culombio (C), aunque se utilizan otras unidades para expresar la carga en términos de la carga elemental (e). La unidad del sistema internacional para la magnitud física m/Q es el kilogramo por culombio (Kg/C).

Espectrometría de masas[editar]

Las unidades y notación anterior se utilizan en la física y en el campo de espectrometría de masas, aunque cuando se presentan los datos de un espectro de masas también es corriente usar la notación m/z como variable.⁴​ Esta notación facilita la interpretación de los datos ya que está más relacionada numéricamente con la unidad de masa atómica del analito.¹​ La m se refiere al número de masa atómica o molecular y z al número de carga del ion. Por ello m/z es una magnitud adimensional. Por ejemplo una molécula doblemente ionizada (z = 2 e) de masa atómica de 1000 unidades (m = 1000 u) con sus dos cargas tendrá m/z = 500.

Historia[editar]

En el siglo XIX se midieron las relaciones masa carga de algunos iones por métodos electroquímicos. En 1897 J. J. Thomson midió por primera vez la relación masa carga del electrón.⁵​ Así demostró que el electrón era una partícula con masa y carga, y que su relación masa carga era mucho más pequeña que la del ion del hidrógeno H⁺. En 1898 Wilhelm Wien separó los iones de los rayos canales según su relación masa carga con un dispositivo óptico iónico que superponía un campos eléctricos y magnéticos (efecto Wien). En 1901 Walter Kaufman midió el incremento de la masa electromagnética de los electrones de alta velocidad (experimentos Kaufmann–Bucherer–Neumann), o incremento de masa relativista en términos modernos. En 1913 Thomson midió la relación masa carga de iones con un instrumento espectrógrafo de parábola.⁶​ Actualmente el instrumento usado para medir la relación masa carga se denomina espectrómetro de masas.

Aplicaciones[editar]

En algunos experimentos la relación carga masa es la única magnitud que se puede medir directamente. Con frecuencia la carga se puede deducir a partir de consideraciones teóricas, así que la relación carga masa proporciona un método para calcular la masa de las partículas.

A menudo la relación carga masa se determina observando la desviación de las partículas cargadas sometidas a un campo magnético externo controlado. La ecuación del ciclotrón, combinada con otra información como la energía cinética de la partícula, nos da la relación carga masa. El espectrómetro de masas se basa en este principio. El mismo principio se utiliza para obtener información en los experimentos que se realizan con la cámara de niebla.

La relación entre las fuerzas electrostáticas con las gravitatorias entre dos partículas puede proporcionar el producto de sus relaciones masa carga. De lo que resulta que las fuerzas gravitatorias son despreciables a nivel subatómico, debido a lo extremadamente pequeñas que son las masas de las partículas subatómicas.

El electrón[editar]

El cociente carga elemental-masa del electrón, ^e⁄_me, es una magnitud fundamental para la física experimental. Es importante porque la masa del electrón, m_e, es difícil de medir directamente, por lo que se obtiene a partir de las medidas de la carga elemental y la relación ^e⁄_me. La relación ^Q⁄_m del electrón fue calculada por primera vez por J. J. Thomson en 1897, con más precisión por Dunnington, mediante cálculos del momento angular y desviaciones debidas a un campo magnético perpendicular. Sus mediciones convencieron a Thomson de que los rayos catódicos eran partículas iguales, y le llevaron a descubrir el electrón.

El CODATA recomendó en 2006 el valor de ^e⁄_me = 1,758820150(44)×10¹¹ C/kg.²​

Se puede medir con el método del tubo de haz fino: se calienta un cátodo para que emita electrones. Los electrones son acelerados por un potencial conocido, para que los electrones tengan una velocidad conocida. La trayectoria del haz puede verse cuando los electrones son acelerados a través del gas de helio enrarecido, ya que algunos electrones chocan hacen que la senda se ilumine. un par de bobinas de Helmholtz producen un campo magnético uniforme y mensurable perpendicular al haz de electrones. Este campo desvía el haz de electrones a una trayectoria circular. Se calcula e/m midiendo el potencial de aceleración (voltios) y la corriente (amperios) de las bobinas de Helmholtz, y el radio del haz de electrones.⁷​

Efecto Zeeman[editar]

La relación carga masa del electrón también puede medirse mediante el efecto Zeeman, que consiste en el desdoblamiento de las líneas de los espectro cuando el elemento está en presencia de un campo magnético B:

${\displaystyle \Delta E={\frac {e\hbar B}{2m}}(m_{j,f}g_{J,f}-m_{j,i}g_{J,i})}$

Aquí m_j son valores cuánticos enteros que oscilan del -j al j, con j como el valor propio del operador del momento angula total angular J, siendo:²​

${\displaystyle \mathbf {J} =\mathbf {L} +\mathbf {S} }$

Donde S es el operador del espín con valor propio s y L es el operador del momento angular con valor propio l. Siendo g_J el factor de Landé, que se calcula así:

${\displaystyle g_{J}=1+{\frac {j(j+1)+s(s+1)-l(l+1)}{2j(j+1)}}}$

El incremento de energía se puede expresar en términos de frecuencia ν y longitud de onda λ:

${\displaystyle \Delta E=h\Delta \nu =hc\Delta \left({\frac {1}{\lambda }}\right)=hc{\frac {\Delta \lambda }{\lambda ^{2}}}}$

Las medias del efecto Zeeman generalmente implican el uso de un interferómetro Fabry-Pérot, con luz proveniente de una fuente situada en un campo magnético que pasa entre los dos espejos del interferómetro. Si δD es el cambio que se necesita para que la separación del espejo para llevar el anillo de orden m (emésimo) de la longitud de onda λ + Δλ a que coincida con el de la longitud de onda λ, y ΔD lleva al anillo (m + 1) de longitud de onda λ a que coincida con el anillo de orden m, entonces:

${\displaystyle \Delta \lambda =\lambda ^{2}{\frac {\delta D}{2D\Delta D}}}$.

Sustituyendo en la anterior:

${\displaystyle hc{\frac {\Delta \lambda }{\lambda ^{2}}}=hc{\frac {\delta D}{2D\Delta D}}={\frac {e\hbar B}{2m}}(m_{j,f}g_{J,f}-m_{j,i}g_{J,i})\ .}$

Operando es posible conseguir la relación carga masa del electrón como:

${\displaystyle {\frac {e}{m}}={\frac {4\pi c}{B(m_{j,f}g_{J,f}-m_{j,i}g_{J,i})}}{\frac {\delta D}{D\Delta D}}\ .}$