CONCEPTOS FÍSICOS

CONCEPTOS FUNDAMENTALES

Onda estacionaria. Los puntos rojos son los nodos de la onda.

Un nodo es un punto en un onda estacionaria donde la onda tiene un amplitud (física) mínima. Por ejemplo, en una cuerda vibrante como la de una guitarra, los extremos de la cuerda son nodos. Al cambiar la posición del nodo final pulsando un traste, el guitarrista cambia la longitud efectiva de la cuerda vibrante y por lo tanto la nota producida. El opuesto de un nodo es un anti-nodo, un punto donde la amplitud de la onda estacionaria es máxima. Estos puntos se sitúan a mitad de camino entre los nodos.

Explicación[editar]

Patrón de la interferencia de dos ondas (de arriba a abajo). El punto representa el nodo.

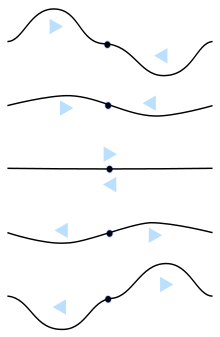
Una onda estacionaria se produce cuando dos trenes de ondas sinusoidales de la misma frecuencia se mueven en direcciones opuestas en el mismo espacio e interfieren entre sí.²​ Se forman cuando las ondas se reflejan en un límite físico, como el sonido reflejado desde una pared o la radiación electromagnética reflejada desde el final de una línea de transmisión, y particularmente cuando las ondas están confinadas en un oscilador en resonancia, rebotando hacia adelante y hacia atrás entre dos límites, como en un tubo de órgano o una cuerda de un instrumento musical.

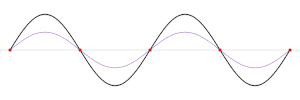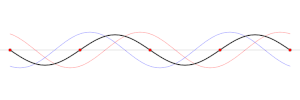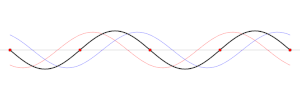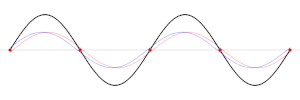
En una onda estacionaria, los nodos son una serie de ubicaciones a intervalos igualmente espaciados donde la amplitud de la onda (y por lo tanto, su movimiento) es cero (véase la animación anterior). En estos puntos, las dos ondas se suman con fases opuestas y se anulan mutuamente. Se localizan a intervalos separados por la mitad de una longitud de onda (λ / 2). A mitad de camino entre cada par de nodos se presentan ubicaciones donde la amplitud es máxima. Estos puntos se llaman antinodos. En estos puntos, las dos ondas se suman con la misma fase y se refuerzan mutuamente.

En los casos en que los dos trenes de onda opuestos no tienen la misma amplitud, no se cancelan a la perfección, por lo que la amplitud de la onda estacionaria en los nodos no es cero, sino simplemente un mínimo. Esto ocurre cuando el reflejo en el límite es imperfecto, lo que se indica mediante una razón de onda estacionaria finita, la relación entre la amplitud de la onda en el antinodo y la amplitud en el nodo.

En la resonancia de una superficie bidimensional o membrana, como un parche de tambor o placa de metal vibrante, los nodos se convierten en líneas nodales, líneas en la superficie donde la superficie está inmóvil, dividiendo la superficie en regiones separadas que vibran con la fase opuesta. Estos pueden hacerse visibles rociando arena en la superficie, y los intrincados patrones de líneas resultantes se llaman patrones de Ernst Chladni.

En líneas de transmisión de corriente alterna, un nodo de voltaje es un antinodo de intensidad y un antinodo de voltaje es un nodo de intensidad.

Los nodos son los puntos de desplazamiento cero, no los puntos donde se cruzan dos ondas constituyentes.

Condiciones de frontera[editar]

La posición de los nodos en relación con el límite que refleja las ondas depende de las condiciones finales, o lo que es lo mismo, se trata de un problema de condición de frontera. Aunque hay muchos tipos de condiciones finales, los extremos de los resonadores suelen ser uno de los dos tipos que provocan una reflexión total:

• Límite fijo: ejemplos de este tipo de límite son el punto de conexión de una cuerda de guitarra, el extremo cerrado de una tubería abierta como un tubo de órgano o un instrumento de viento-madera, la periferia de un parche de tambor, una línea de transmisión con el extremo cortocircuitado o los espejos en los extremos de una cavidad óptica. En este tipo, la amplitud de la onda se fuerza a cero en el límite, por lo que hay un nodo en el límite, y los otros nodos se producen en múltiplos de la mitad de una longitud de onda de la misma:

0, λ / 2, λ, 3λ / 2, 2λ, ...

• Límite libre: Ejemplos de este tipo son un órgano de extremo abierto o un tubo de viento de madera, los extremos de las barras del resonador vibratorio en un xilófono, glockenspiel o diapasón, los extremos de una antena o una línea de transmisión con un extremo abierto. En este tipo, la derivada (pendiente) de la amplitud de la onda (en sonido, la presión, en ondas electromagnéticas, la intensidad) se fuerza a cero en el límite. Entonces hay un máximo de amplitud (antinodo) en el límite, el primer nodo se produce a una cuarta parte de la longitud de onda desde el final, y los otros nodos se encuentran a la mitad de los intervalos de longitud de onda desde allí:

λ / 4, 3λ / 4, 5λ / 4, 7λ / 4, ...

Ejemplos[editar]

Onda estacionaria, como suma de dos ondas opuestas

Sonido[editar]

Una onda de sonido consiste en ciclos alternados de compresión y expansión del medio de onda. Durante la compresión, las moléculas del medio se fuerzan a juntarse, lo que se traduce en una mayor presión y densidad. Durante la expansión, las moléculas se separan, lo que produce la disminución de la presión y la densidad.

La cantidad de nodos en una longitud especificada es directamente proporcional a la frecuencia de la onda.

Ocasionalmente, en una guitarra, violín u otro instrumento de cuerda, los nodos se usan para crear armónicos. Cuando el dedo se coloca en la parte superior de la cuerda en cierto punto, pero no se lleva hasta el traste, se crea un tercer nodo (adicional a los formados en el puente y en la cejilla) y se emite un armónico. Durante la interpretación normal, cuando se usan los trastes, los armónicos están siempre presentes, aunque son menos sonoros. Con el método de nodo artificial, el sobretono es más fuerte y el tono fundamental es más tenue. Si el dedo se coloca en el punto medio de la cuerda, se escucha el primer sobretono, que está una octava por encima de la nota fundamental que se tocaría, si el armónico no suene. Cuando dos nodos adicionales dividen la cuerda en tercios, esto crea una octava y un quinto perfecto (duodécimo). Cuando tres nodos adicionales dividen la cuerda en cuartos, esto crea una doble octava. Cuando cuatro nodos adicionales dividen la cuerda en quintas, esto crea una octava doble y una tercera mayor (17ma). La octava, el tercio principal y el quinto perfecto son las tres notas presentes en un acorde mayor.

El sonido característico que permite al oyente identificar un instrumento en particular se debe en gran parte a la magnitud relativa de los armónicos creados por el instrumento.

Química[editar]

En química, las ondas u "orbitales" según la mecánica cuántica, se usan para describir las propiedades ondulatorias de los electrones. Muchas de estas ondas cuánticas también tienen nodos y antinodos. El número y la posición de estos nodos y antinodos dan lugar a muchas de las propiedades de un átomo o enlace covalente. Los orbitales atómicos se clasifican según el número de nodos radiales y angulares, mientras que los orbitales moleculares se clasifican de acuerdo con el carácter de vinculación. Los orbitales moleculares con un antinodo entre los núcleos son muy estables y se conocen como "orbitales de unión" que fortalecen el vínculo. En contraste, los orbitales moleculares con un nodo entre los núcleos no serán estables debido a la repulsión electrostática y se conocen como "orbitales antiadherentes", que debilitan el enlace. Otro concepto de mecánica cuántica es el de partícula en una caja, donde el número de nodos de la función de onda puede ayudar a determinar el estado de energía cuántica: los nodos cero corresponden al estado fundamental, un nodo corresponde al primer estado excitado, etc. En general,³​ organiza los autoestados en el orden de las energías crecientes,${\displaystyle \epsilon _{1},\epsilon _{2},\epsilon _{3},...}$, las funciones propias también caen en el orden de un número creciente de nodos; la enésima función propia tiene n-1 nodos, entre cada uno de los cuales las siguientes funciones propias tienen al menos un nodo.

observador es cualquier ente capaz de realizar mediciones de magnitudes físicas de un sistema físico para obtener información sobre el estado físico de dicho sistema.

Por "abuso de lenguaje" también se denomina observador a la descripción matemática de uno de esos entes capaces de hacer medidas. Dados dos observadores, un problema fundamental es establecer las leyes de transformación (o covariancia general) necesarias para relacionar las medidas de ambos observadores.

Observadores en Mecánica clásica[editar]

Los observadores en mecánica clásica tienen dos propiedades fundamentales:

1. Tiempo absoluto. Todos los obsevadores comparten una referencia temporal, o tiempo absoluto, es decir, existe una magnitud escalar llamada tiempo que tiene el mismo valor invariante para todos los observadores con independencia de su estado de movimiento.
2. Discrecionalidad de la medida. Es posible concebir, al menos en la teoría, un procedimiento de medida arbitrariamente exacto, tal que cualquiera que sea la magnitud física observada en el proceso de medición no altera el estado físico. Es decir, pueden tratarse discrecionalmente al observador y al sistema físico observado.

Mecánica newtoniana[editar]

En mecánica newtoniana un observador es cualquier sujeto o aparato de medir asociado a un sistema de referencia cartesiano (aunque podemos definir sistemas de referencia no cartesianos, no suelen usarse en el marco de la mecánica newtoniana). Además en mecánica newtoniana existen un tipo de observadores "privilegiados" llamados observadores inerciales (aunque un sistema de referencia cartesiano puede ser inercialo no-inercial).

Los sistemas de referencia inerciales tienen la peculiaridad de que en ellos se satisfacen directamente las leyes de Newton. En cambio en los sistemas no-inerciales, la suma de fuerzas reales no iguala al producto de la masa por la aceleración de la partícula. De hecho un observador no-inercial que tratara de estudiar el movimiento de una partícula a partir de las leyes de Newton se vería obligado a introducir ciertas fuerzas aparentes o fuerzas ficticias que sumadas a las fuerzas reales si verificarían entonces las leyes de Newton.

Mecánica de medios continuos[editar]

En el estudio de la deformación en la mecánica de medios continuos se emplean comúnmente dos sistemas de coordenadas diferentes:

• Las coordenadas lagrangianas o materiales.
• Las coordenadas eulerianas o espaciales.

Observadores en Mecánica relativista[editar]

De las dos propiedades fundamentales de los observadores de la mecánica clásica, la propiedad del tiempo absoluto y la discrecionalidad de la medida, en mecánica relativista sólo se mantiene la segunda, ya que debido al carácter relativo del espacio y el tiempo de los observadores, no puede definirse un tiempo absoluto independiente del observador, sino que cada uno tiene su tiempo propio.

En mecánica relativista un observador de una región del espacio-tiempo viene caracterizado por una sección del fibrado de bases ortonormales del espacio tangente a cada punto [de la variedad diferenciable que representa] el espacio-tiempo curvo. Así un observador sería una asignación a cada punto del espacio tiempo de cuatro campos vectoriales continuos mutuamente ortogonales, que representarían los "ejes de coordenadas" usados para ese punto. Matemáticamente estos campos vectoriales forman un marco móvil. La condición de que el observador sea físicamente realizable, mediante instrumentos y aparatos de medida, es que uno estos campos vectoriales sea para todo punto del espacio-tiempo un vector temporal. Un observador por tanto podría representarse sobre una región con coordenadas x^μ como:

${\displaystyle \left\{e_{0}(x^{\mu }),e_{1}(x^{\mu }),e_{2}(x^{\mu }),e_{3}(x^{\mu })\right\}_{obs}}$

Donde:

${\displaystyle g(e_{0},e_{0})<0 annotation="" e_="" g="" i="" in="" left="" qquad="" quad="" right="">$

La objetvidad física del espacio-tiempo, o más propiamente intersubjetividad de las medidas, implica que al ser observado un mismo fenómeno físico por diferentes observadores las medidas realizadas por estos deben ser relacionables por reglas fijas, conocidas como leyes de transformación acordes a si la magnitud física es de tipo escalar, vectorial o propiamente tensorial.

Si los sistemas de ejes ortogonales usados por dos observadores vienen dados por ${\displaystyle \left\{{\hat {e}}_{0},{\hat {e}}_{1}{\hat {e}}_{2},{\hat {e}}_{3}\right\}_{obs1}}$ y ${\displaystyle \left\{{\bar {e}}_{0},{\bar {e}}_{1}{\bar {e}}_{2},{\bar {e}}_{3}\right\}_{obs2}}$, las componentes físicas de un tensor cualquiera T vendrán dadas por en los dos sistemas de coordenadas serán diferentes:

${\displaystyle T={\hat {T}}_{\alpha _{1},...\alpha _{m}}^{\beta _{1}...\beta _{n}}\quad {\hat {e}}_{\alpha _{1}}\otimes ...\otimes {\hat {e}}_{\alpha _{m}}\otimes {\hat {\theta }}^{\beta _{1}}\otimes ...\otimes {\hat {\theta }}^{\beta _{n}}}$

${\displaystyle T={\bar {T}}_{\alpha _{1},...\alpha _{m}}^{\beta _{1}...\beta _{n}}\quad {\bar {e}}_{\alpha _{1}}\otimes ...\otimes {\bar {e}}_{\alpha _{m}}\otimes {\bar {\theta }}^{\beta _{1}}\otimes ...\otimes {\bar {\theta }}^{\beta _{n}}}$

${\displaystyle {\hat {T}}_{\alpha _{1},...\alpha _{m}}^{\beta _{1}...\beta _{n}}\neq {\bar {T}}_{\alpha _{1},...\alpha _{m}}^{\beta _{1}...\beta _{n}}}$

Donde hemos usado el convenio de sumación de Einstein y:
${\displaystyle \left\{{\hat {\theta }}^{0},{\hat {\theta }}^{1}{\hat {\theta }}^{2},{\hat {\theta }}^{3}\right\}_{obs1}}$, base dual de ${\displaystyle \left\{{\hat {e}}_{0},{\hat {e}}_{1}{\hat {e}}_{2},{\hat {e}}_{3}\right\}_{obs1}}$, definida por: ${\displaystyle {\hat {\theta }}^{\beta }({\hat {e}}_{\alpha })=\delta _{\alpha }^{\beta }}$.
${\displaystyle \left\{{\bar {\theta }}^{0},{\bar {\theta }}^{1}{\bar {\theta }}^{2},{\bar {\theta }}^{3}\right\}_{obs2}}$, base dual de ${\displaystyle \left\{{\bar {e}}_{0},{\bar {e}}_{1}{\bar {e}}_{2},{\bar {e}}_{3}\right\}_{obs2}}$, definida por: ${\displaystyle {\bar {\theta }}^{\beta }({\bar {e}}_{\alpha })=\delta _{\alpha }^{\beta }}$

Sin embargo, las componentes medidas por el observador 1 y el observador 2 por el principio de objetividad de la realidad física estarán relacioandas de la siguiente manera (nuevamente se usa la convención de Einstein):

${\displaystyle {\bar {T}}_{\alpha _{1},...\alpha _{m}}^{\beta _{1}...\beta _{n}}={\hat {T}}_{\alpha '_{1},...\alpha '_{m}}^{\beta '_{1}...\beta '_{n}}\quad {A^{T}}_{\beta '_{1}}^{\beta _{1}}...{A^{T}}_{\beta '_{n}}^{\beta _{n}}A_{\alpha _{1}}^{\alpha '_{1}}...A_{\alpha _{n}}^{\alpha '_{n}}}$

Donde A representa la matriz cambio de base, entre las bases vectoriales dadas para el observador 1 y el observador 2. Por ejemplo si consideramos sólo observadores inerciales dentro de la teoría de la relatividad especial la matriz A es simplemente una transformación de Lorentz.

Observadores en Mecánica cuántica[editar]

En mecánica cuántica de los dos supuestos fundamentales de los observadores de la mecánica clásica, el de discrecionalidad de la medida resulta inaceptable (en cambio el del tiempo absoluto es usado en mecánica cuántica no relativista, pero no es aceptable en mecánica cuántica relativista).

La falta de discrecionalidad de la medida ocasiona complicaciones, recogidas en los postulados III y IV y que en conjunto afirman que el resultado de una magnitud física no tiene que tener un valor determinado y fijo para un observador. El resultado de una medida es una variable aleatoria aunque su distribución de probabilidad generalmente sí es conocida, además durante el proceso de medida el sistema experimenta una evolución no determinista e impredictible (en el intervalo entre medidas en cambio el sistema evoluciona de acuerdo con la ecuación de Schrödinger tal como afirma el postulado V).