GEOMETRÍA

FIGURAS GEOMÉTRICAS - CURVAS

Recta secante que corta una circunferencia .

Secantes, cuerdas y tangentes de la circunferencia.

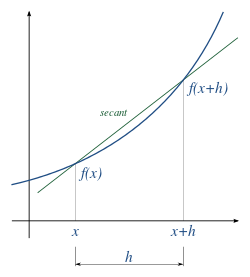
Una recta secante (lat. secare "cortar") es una recta que corta a una circunferencia en 2 puntos. Conforme estos puntos se acercan y su distancia se reduce a cero, la recta adquiere el nombre de recta tangente.

Dados los puntos de intersección A y B puede calcularse la ecuación de la recta secante. Para ello en matemáticas se emplea la ecuación de la recta que pasa por dos puntos:

${\displaystyle y={\frac {y_{A}-y_{B}}{x_{A}-x_{B}}}x+{\frac {x_{A}y_{B}-x_{B}y_{A}}{x_{A}-x_{B}}}}$

Un sector hiperbólico es una región del plano cartesiano {(x,y)} delimitada por los rayos desde el origen a dos puntos (a, 1/a) y (b, 1/b) y la hipérbola xy = 1.¹​

En un sector hiperbólico en posición estándar a = 1 y b > 1 .

El área de un sector hiperbólico en posición estándar es el log_e b . (Demostración: Integrar bajo la curva 1/x entre 1 y b, y sumarle el área del triángulo {(0, 0), (1, 0), (1, 1)}, y restarle el área del triángulo {(0, 0), (b, 0), (b, 1/b)} )

Cuando un sector hiperbólico se encuentra en posición estándar el mismo se corresponde con un ángulo hiperbólico positivo.

Parámetros de una elipse. El semieje mayor está representado aquí por a, que corresponde a la misma distancia entre el centro de la elipse y los puntos A y B, es decir, la mitad del eje mayor.

En matemáticas, el semieje mayor de una elipse es la mitad del diámetro más largo; su símbolo es a. En astronomía, es equivalente a la distancia media de un objeto que orbita alrededor de otro, ya que el objeto central (por ejemplo, el Sol) ocupa uno de los focos.

Astronomía[editar]

El semieje mayor es una de las características más importantes de una órbita, junto con su período orbital. Puede ser matemáticamente probado que para un cuerpo orbitando, el semieje mayor representa la distancia media del cuerpo a la fuente central gravitacional. Para los objetos del Sistema Solar, el semieje mayor está relacionado con el período de la órbita por la tercera ley de Kepler, originalmente descrita como:

${\displaystyle P^{2}=ka^{3}\,}$

donde P es el período medido en años, a es el semieje mayor medido en unidades astronómicas y k una constante de proporcionalidad.

Esta fórmula fue modificada por Newton al desarrollar su teoría gravitatoria, expresándola como:

${\displaystyle P^{2}={\frac {4\pi ^{2}}{GM}}a^{3}}$

donde G es la Constante de gravitación universal y M es la masa del cuerpo central.

Parámetros de una elipse. El semieje menor: b

Semi-latus rectum (ℓ) de una elipse.

En matemáticas, el semieje menor de una elipse es la mitad del diámetro más corto; su símbolo es b.

De la definición de elipse, el extremo del eje menor equidista de los focos y dichas distancias (F₁-C y F₂-C) equivalen a la medida del semieje mayor a.

El centro de la elipse, el foco y el extremo del semieje menor conforman un triángulo rectángulo. Aplicando el Teorema de Pitágoras:

${\displaystyle a^{2}=b^{2}+c^{2}\,}$

donde c es la semi-distancia focal.

Como la excentricidad es: ${\displaystyle e={\frac {c}{a}}}$, su relación será:

${\displaystyle b=a\cdot {\sqrt {1-e^{2}}}}$

${\displaystyle b^{2}=al\,\!}$

donde (ℓ) es el semi-latus rectum de una elipse.

seno del topólogo, en topología, es una curva contenida en ${\displaystyle \mathbb {R} ^{2}}$ utilizada frecuentemente para ilustrar determinadas propiedades de los espacios topológicos.¹​ Se utiliza especialmente a modo de ejemplo de espacio topológico que es conexo pero no conexo por caminos.

Una definición usual del seno del topólogo es la adherencia de la curva

${\displaystyle A=\{(x,{\mbox{sen}}({\tfrac {1}{x}})),\ x\in (0,1]\}}$,

denotada ${\displaystyle {\bar {A}}}$, y que se define a su vez como la unión de ${\displaystyle A}$ con su frontera, el segmento

${\displaystyle \partial A=\{(0,y),\ y\in [-1,1]\}}$

A medida que x se acerca a cero, 1/x crece cada vez más rápido (de hecho, tiende a infinito), por lo que la frecuencia de la curva sinusoidal también es cada vez mayor. En el límite, la frecuencia es infinita.

Variantes[editar]

En ocasiones, se considera solamente ${\displaystyle A}$, o la unión de ${\displaystyle A}$ con el punto ${\displaystyle (0,0)}$. También se puede considerar la función ${\displaystyle f(x)={\mbox{sen}}({\tfrac {1}{x}})}$ definida en un intervalo distinto de (0,1],²​ aunque siempre en un intervalo abierto en 0. Incluso se puede hacer distinción entre la «curva cerrada» (${\displaystyle {\bar {A}}}$) y la «curva abierta» (${\displaystyle A}$) del seno del topólogo.¹​

Propiedades[editar]

La función ${\displaystyle f(x)={\mbox{sen(1/x)}},f(0)=0}$ no es de variación acotada.

Como adherencia de un conjunto conexo, ${\displaystyle {\bar {A}}}$ es un conjunto conexo. Sin embargo, no es conexo por caminos, pues no existe un camino ${\displaystyle f:[0,1]\rightarrow {\bar {A}}}$ que una los puntos ${\displaystyle (1,{\mbox{sen}}(1))}$ y ${\displaystyle (0,0)}$. Para ver que es así, considérese la sucesión formada por los puntos, tomados de derecha a izquierda en la gráfica, cuya segunda componente es alternativamente +1 ó -1. Esta sucesión no converge.