GEOMETRÍA

FIGURAS GEOMÉTRICAS - CURVAS

curva hipocicloide es la trayectoria descrita por un punto situado sobre una circunferenciageneratriz que rueda sin deslizar por el interior de otra circunferencia directriz, sin deslizamiento. Es un tipo de ruleta cicloidal.

La curva hipocicloide es comparable a la cicloide, donde la circunferencia generatriz rueda sobre una línea directriz (o circunferencia de radio infinito).

La curva roja es una hipocicloide dibujada al girar la circunferencia negra pequeña por el interior de la circunferencia azul grande, obteniendo en este caso una deltoide).

Las ecuaciones paramétricas de una curva hipocicloide generada por un punto de una circunferencia de radio ${\displaystyle r_{2}}$ que rueda dentro de una circunferencia de radio ${\displaystyle r_{1}}$, son:

${\displaystyle x=(r_{1}-r_{2})\cos \alpha \ +r_{2}\ \sin \gamma }$               (1)

${\displaystyle y=(r_{1}-r_{2})\sin \alpha \ -r_{2}\ \cos \gamma }$               (2)

Donde ${\displaystyle \alpha }$ es el ángulo con el que varía ${\displaystyle r_{1}}$ y el eje ${\displaystyle x}$, y ${\displaystyle \gamma }$ es el ángulo que varía entre la línea imaginada de proyección sobre el eje ${\displaystyle x}$ del centro del círculo de radio ${\displaystyle r_{2}}$ y dicho radio.

Pero,

${\displaystyle \displaystyle \beta +\gamma +{\frac {\pi }{2}}-\alpha =\pi }$

${\displaystyle \displaystyle \gamma ={\frac {\pi }{2}}+\alpha -\beta }$               (3)

donde ${\displaystyle \beta }$ es un ángulo que varía entre ${\displaystyle r_{2}}$ y el segmento de ${\displaystyle r_{1}}$ donde se genera un vértice con el punto centro del círculo de circunferencia generatriz. Además, como la circunferencia rueda sin deslizamiento, los arcos ${\displaystyle l_{1}}$ y ${\displaystyle l_{2}}$son iguales, es decir: ${\displaystyle r_{1}\ \alpha =l_{1}=l_{2}=r_{2}\ \beta }$. De aquí se tiene que ${\displaystyle \displaystyle \beta ={\frac {r_{1}}{r_{2}}}\alpha }$

Sustituyendo ${\displaystyle \beta }$ en la ecuación (3), y esta última en (1) y (2) se obtienen las siguientes ecuaciones paramétricas de la hipocicloide:

${\displaystyle x=(r_{1}-r_{2})\cos \alpha \ +r_{2}\ \cos \left[\alpha \left(1-{\frac {r_{1}}{r_{2}}}\right)\right]}$

${\displaystyle y=(r_{1}-r_{2})\sin \alpha \ +r_{2}\ \sin \left[\alpha \left(1-{\frac {r_{1}}{r_{2}}}\right)\right]}$

Casos particulares[editar]

Cuando ${\displaystyle {\frac {r_{1}}{r_{2}}}=k}$ es un número racional, es decir, ${\displaystyle \displaystyle {\frac {r_{1}}{r_{2}}}={\frac {p}{q}}}$, siendo p y q números enteros, las hipocicloides son curvas algebraicas.

Cuando r₁=4 r₂ se tiene la astroide (x^2/3+y^2/3=R^2/3)

Si ${\displaystyle \displaystyle {\frac {r_{1}}{r_{2}}}}$ es irracional, la curva es trascendente y da infinitas vueltas dentro de la circunferencia directriz.

Ejemplos[editar]

• 

  k=3
 
• 

  k=4
 
• 

  k=5
 
• 

  k=6
• 

  k=2.1
 
• 

  k=3.8
 
• 

  k=5.5
 
• 

  k=7.2

• Las curvas hipocicloides son una clase especial de hipotrocoides, las cuales a su vez son una clase particular de ruleta.
• La hipocicloide de tres puntas se denomina curva deltoide.
• La hipocicloide de cuatro puntas se llama astroide.

En la hipocicloide la ruleta y la directriz son curvas tangentes interiores, por tanto, para su trazado debemos repasar los contenidos y procedimientos sobre este tipo de tangencias.
Como ocurre con la cicloide y la epicicloide, la hipocicloide puede ser de tres tipos: normal , acortada y alargada.
En la imagen superior puedes ver las tres clases de hipocicloides.

longitud de arco, también llamada rectificación de una curva, es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. Históricamente, ha sido difícil determinar esta longitud en segmentos irregulares; aunque fueron usados varios métodos para curvas específicas. La llegada del cálculo trajo consigo la fórmula general para obtener soluciones cerradas para algunos casos.

Cálculo mediante integrales[editar]

Al considerar una curva definida por una función ${\displaystyle f\left(x\right)}$ y su respectiva derivada ${\displaystyle f'\left(x\right)}$ que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:

(1)${\displaystyle s=\int _{a}^{b}{\sqrt {1+\left[f'\left(x\right)\right]^{2}}}\,dx}$

En el caso de una curva definida paramétricamente mediante dos funciones dependientes de t como ${\displaystyle x=f\left(t\right)}$ e ${\displaystyle y=g\left(t\right)}$, la longitud del arco desde el punto ${\displaystyle (f(a),g(a))\,}$ hasta el punto ${\displaystyle (f(b),g(b))\,}$ se calcula mediante:

(2)${\displaystyle s=\int _{a}^{b}{\sqrt {\left[f'\left(t\right)\right]^{2}+\left[g'\left(t\right)\right]^{2}}}\,dt}$

Si la función está definida por coordenadas polares donde la coordenadas radial y el ángulo polar están relacionados mediante ${\displaystyle r=f(\theta )\,}$, la longitud del arco comprendido en el intervalo ${\displaystyle [\alpha ,\beta ]\,}$, toma la forma:

(3)${\displaystyle s=\int _{\alpha }^{\beta }{\sqrt {[f(\theta )]^{2}+\left[f'(\theta )\right]^{2}}}\,d\theta \ }$

En la mayoría de los casos, no hay una solución cerrada disponible y será necesario usar métodos de integración numérica. Por ejemplo, aplicar esta fórmula a la circunferencia de una elipse llevará a una integral elíptica de segunda especie. Entre las curvas con soluciones cerradas están la catenaria, el círculo, la cicloide, la espiral logarítmica, la parábola, la parábola semicúbica y la línea recta.

Un caso un poco más general que el último, es el caso de coordenadas curvilíneas generales (e incluso el de espacios no euclídeos) caracterizadas por un tensor métrico ${\displaystyle g_{ik}}$ donde la longitud de una curva ${\displaystyle C:[a,b]\to M}$viene dada por:

(4)${\displaystyle s=\int _{a}^{b}{\sqrt {\sum _{i,k}g_{ik}{\frac {dx^{i}}{dt}}{\frac {dx^{k}}{dt}}}}\ dt}$

Por ejemplo el caso de coordenadas polares se obtiene de este haciendo ${\displaystyle x^{1}=r,x^{2}=\theta ;g_{11}=1,g_{22}=r^{2},g_{12}=g_{21}=0;r=f(\theta ),t=\theta }$.

Ejemplos de cálculo[editar]

El perímetro de una circunferencia de radio R puede calcularse a partir de la ecuación de esta curva en coordenadas polares

${\displaystyle f(\theta )=R,\quad 0\leq \theta \leq 2\pi }$

Para calcular el perímetro se utiliza entonces la ecuación (3)

${\displaystyle s=\int _{0}^{2\pi }{\sqrt {[f(\theta )]^{2}+\left[f'(\theta )\right]^{2}}}\,d\theta \ =R\int _{0}^{2\pi }\,d\theta =2\pi R}$

Se obtiene que el perímetro de una circunferencia es proporcional al diámetro, lo que se corresponde con la definición de pi.

Para determinar la longitud de un arco de circunferencia, basta restringir el ángulo de barrido de la curva a un intervalo más pequeño.

${\displaystyle f(\theta )=R,\quad \theta _{0}\leq \theta \leq \theta _{1}}$

La longitud del arco queda

${\displaystyle s=\int _{\theta _{0}}^{\theta _{1}}{\sqrt {[f(\theta )]^{2}+\left[f'(\theta )\right]^{2}}}\,d\theta \ =R\cdot (\theta _{1}-\theta _{0})}$

Deducción de la fórmula para funciones de una variable[editar]

Aproximación por múltiples segmentos lineales.

Para un pequeño segmento de curva, Δs se puede aproximar con el teorema de Pitágoras.

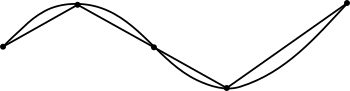
Suponiendo que se tiene una curva rectificablecualquiera, determinada por una función ${\displaystyle f\left(x\right)}$, y suponiendo que se quiere aproximar la longitud del arco de curva ${\displaystyle s}$ que va desde un punto ${\displaystyle a}$ a uno ${\displaystyle b}$. Con este propósito es posible diseñar una serie de triángulos rectángulos cuyas hipotenusas concatenadas "cubran" el arco de curva elegido tal como se ve en la figura. Para hacer a este método "más funcional" también se puede exigir que las bases de todos aquellos triángulos sean iguales a ${\displaystyle \Delta x}$, de manera que para cada uno existirá un cateto ${\displaystyle \Delta y}$asociado, dependiendo del tipo de curva y del arco elegido, siendo entonces cada hipotenusa, ${\displaystyle \Delta s={\sqrt {\Delta x^{2}+\Delta y^{2}}}}$, al aplicarse el teorema de Pitágoras. Así, una aproximación de ${\displaystyle s}$ estaría dada por la sumatoria de todas aquellas ${\displaystyle n}$ hipotenusas desplegadas. Por eso se tiene que:

${\displaystyle s\approx \sum _{i=1}^{n}{\sqrt {\Delta x_{i}^{2}+\Delta y_{i}^{2}}}}$

Pasando a operar algebraicamente la forma en la que se calcula cada hipotenusa para llegar a una nueva expresión;

${\displaystyle {\sqrt {\Delta x^{2}+\Delta y^{2}}}={\sqrt {({\Delta x^{2}+\Delta y^{2}})\left({\frac {\Delta x^{2}}{\Delta x^{2}}}\right)}}={\sqrt {1+\left({\frac {\Delta y^{2}}{\Delta x^{2}}}\right)}}\Delta x={\sqrt {1+\left({\frac {\Delta y}{\Delta x}}\right)^{2}}}\Delta x}$

Luego, el resultado previo toma la siguiente forma:

${\displaystyle s\approx \sum _{i=1}^{n}{\sqrt {1+\left({\frac {\Delta y_{i}}{\Delta x_{i}}}\right)^{2}}}\Delta x_{i}}$

Ahora bien, mientras más pequeños sean estos ${\displaystyle n}$ segmentos, mejor será la aproximación buscada; serán tan pequeños como se desee, de modo que ${\displaystyle \Delta x}$ tienda a cero. Así, ${\displaystyle \Delta x}$ se convierte en ${\displaystyle dx}$, y cada cociente incremental ${\displaystyle {\Delta y_{i}/\Delta x_{i}}}$ se transforma en un ${\displaystyle dy/dx}$ general, que es por definición ${\displaystyle f'\left(x\right)}$. Dados estos cambios, la aproximación anterior se convierte en una sumatoria más fina y ahora exacta, una integración de infinitos segmentos infinitesimales;

${\displaystyle s=\lim _{\Delta x_{i}\to 0}\sum _{i=1}^{\infty }{\sqrt {1+\left({\frac {\Delta y_{i}}{\Delta x_{i}}}\right)^{2}}}\Delta x_{i}=\int _{a}^{b}{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}dx=\int _{a}^{b}{\sqrt {1+\left[f'\left(x\right)\right]^{2}}}\,dx}$

Métodos anteriores al cálculo[editar]

Antigüedad[editar]

A través de la historia de las matemáticas, grandes pensadores consideraron imposible calcular la longitud de un arco irregular. Aunque Arquímedes había descubierto una aproximación rectangular para calcular el área bajo una curva con un método de agotamiento, pocos creyeron que fuera posible que una curva tuviese una longitud definida, como las líneas rectas. Las primeras mediciones se hicieron posibles, como ya es común en el cálculo, a través de aproximaciones: los matemáticos de la época trazaban un polígono dentro de la curva, y calculaban la longitud de los lados de éste para obtener un valor aproximado de la longitud de la curva. Mientras se usaban más segmentos, disminuyendo la longitud de cada uno, se obtenía una aproximación cada vez mejor.

Siglo XVII[editar]

En esta época, el método de agotamiento llevó a la rectificación por métodos geométricos de muchas curvas trascendentales: la Espiral logarítmica de Torricelli en 1645 (algunos piensan que fue John Wallis en 1650), el Cicloide de Christopher Wren en 1658, y la Catenaria de Gottfried Leibniz en 1691.