GEOMETRÍA

FIGURAS GEOMÉTRICAS - CURVAS

circunferencia hiperbólica, hiperciclo, hipercírculo o curva equidistante hiperbólica es una curva cuyos puntos tienen la misma distancia ortogonal desde una recta determinada (su eje).

Dada una línea recta L y un punto P externo a L, se puede construir un hiperciclo tomando todos los puntos Q en el mismo lado de L que P, con una distancia perpendicular a L igual a la de P.

La línea L se denomina eje, centro o línea base del hiperciclo.

Las líneas perpendiculares al eje, que también es perpendicular al hiperciclo se llaman normales del hiperciclo.

Los segmentos de la normal entre el eje y el hiperciclo se llaman radios.

Su longitud común se llama distancia o radio del hyperciclo.¹​

Los hiperciclos a través de un punto dado que comparten una tangente a través de ese punto convergen hacia un horociclo a medida que sus distancias tienden hacia el infinito.

Propiedades similares a las de las líneas euclidianas[editar]

Los hiperciclos en geometría hiperbólica tienen algunas propiedades similares a las de las líneas rectas en la geometría euclidiana:

• En un plano, dada una recta y un punto exterior a ella, solo existe un hiperciclo de la línea dada (compárese con el axioma de Playfair para la geometría euclidiana).
• No existen tres puntos de un hiperciclo en un círculo.
• Un hiperciclo es simétrico a cada línea perpendicular a él (la imagen especular de un hiperciclo sobre una recta perpendicular al hiperciclo es el mismo hiperciclo).

Propiedades similares a las de las circunferencias euclidianas[editar]

Los hiperciclos en geometría hiperbólica tienen algunas propiedades similares a las de las circunferencias en la geometría euclidiana:

• Una línea perpendicular a la cuerda de un hiperciclo en su punto medio es un radio y bisecta el arco subtendido por la cuerda.

  Sea AB la cuerda y M su punto medio.

  Por simetría, la recta R por M perpendicular a AB debe ser ortogonal al eje L.

  Por lo tanto, R es un radio.

  También por simetría, R bisecará el arco AB.

• El eje y la distancia de un hiperciclo están determinados de forma única.

  Supóngase que un hiperciclo C tiene dos ejes diferentes, L₁ y L₂.

  Usando la propiedad anterior dos veces con diferentes cuerdas se pueden determinar dos radios distintos R₁ y R₂. R₁ y R₂ tendrán que ser perpendiculares a L₁ y L₂, resultando un rectángulo. Esto es una contradicción porque el rectángulo es una figura imposible en geometría hiperbólica.

• Dos hiperciclos tienen las mismas distancias bicondicionalmente congruentes.

  Si tienen la misma distancia, solo se necesita hacer coincidir los ejes para que coincidan con un movimiento rígido y también todos los radios coincidirán; dado que la distancia es la misma, también los puntos de los dos hiperciclos coincidirán.

  Viceversa, si son congruentes, la distancia debe ser la misma que en la propiedad anterior.

• Una línea recta corta un hiperciclo en un máximo de dos puntos.

  Sea la línea K que corta al hiperciclo C en dos puntos A y B. Como antes, se puede construir el radio R de C a través del punto medio M de AB. Téngase en cuenta que K es ultraparalelo respecto al eje L porque están a la distancia R sobre la perpendicular común. Además, dos líneas ultraparalelas tienen una distancia mínima sobre la perpendicular común y la función monótona aumentan a medida que se alejan de la perpendicular.

  Esto significa que los puntos de K dentro de AB tendrán una distancia desde L más pequeña que la distancia común de A y B desde L, mientras que los puntos de K fuera de AB tendrán una distancia mayor. En conclusión, ningún otro punto de K puede estar en C.

• Dos hiperciclos se cruzan en un máximo de dos puntos.

  Sean C₁ y C₂ dos hiperciclos que se cruzan en tres puntos A, B y C.

  Si R₁ es la línea ortogonal a AB a través de su punto medio, se sabe que es un radio de C₁ y C₂.

  Del mismo modo, se construye R₂, el radio a través del punto medio de BC.

  R₁ y R₂ son simultáneamente ortogonales a los ejes L₁ y L₂ de C₁ y C₂, respectivamente.

  Ya se probó que L₁ y L₂ deben coincidir (de lo contrario, se generaría un rectángulo).

  Entonces C₁ y C₂ tienen el mismo eje y al menos un punto común, y por lo tanto, poseen la misma distancia y coinciden.

• No hay tres puntos de un hiperciclo colineales.

  Si los puntos A, B y C de un hiperciclo son colineales, entonces las cuerdas AB y BC están en la misma línea K. Sean R₁ y R₂ los radios a través de los puntos medios de AB y BC. Se sabe que el eje L del hiperciclo es la perpendicular común de R₁ y R₂.

  Pero K es esa perpendicular común. Por lo tanto, la distancia debe ser 0 y el hiperciclo degenera en una línea.

Otras propiedades[editar]

• La longitud de un arco de un hiperciclo entre dos puntos es:
  • Más larga que la longitud del segmento de línea entre esos dos puntos
  • Más corta que la longitud del arco de uno de los dos horociclos entre esos dos puntos
  • Más corta que cualquier arco circular entre esos dos puntos
• Un hiperciclo y un horociclo se cruzan en un máximo de dos puntos.

Longitud del arco[editar]

En el plano hiperbólico de curvatura de Gauss constante -1, la longitud de un arco de un hiperciclo se puede calcular a partir del radio r y la distancia entre los puntos donde las normales se intersecan con el eje d usando la fórmula l = d cosh r.²​

Construcción[editar]

En el disco de Poincaré del plano hiperbólico, los hiperciclos están representados por líneas y arcos circulares que se cruzan con el círculo límite en ángulos no rectos. La representación del eje interseca el círculo límite en los mismos puntos, pero en ángulo recto.

En el modelo del semiplano de Poincaré del plano hiperbólico, los hiperciclos están representados por líneas y arcos circulares que se cruzan con la línea límite en ángulos no rectos. La representación del eje interseca la línea límite en los mismos puntos, pero en ángulo recto.

Ejemplo de cisoide media.

Se llama cisoide a la curva generada por la suma, diferencia o semisuma de los vectores posición de dos curvas dadas.

Sean C₁ y C₂ dos curvas definidas por las siguientes ecuaciones en coordenadas polares:

${\displaystyle \rho =\rho _{1}(\theta )\,}$ y ${\displaystyle \rho =\rho _{2}(\theta )\,}$

Entonces, C₁ y C₂ generan las tres cisoides de ecuaciones:

${\displaystyle \rho =\rho _{1}(\theta )+\rho _{2}(\theta )\,}$

${\displaystyle \rho =\rho _{1}(\theta )-\rho _{2}(\theta )\,}$

${\displaystyle \rho ={\frac {\rho _{1}(\theta )+\rho _{2}(\theta )}{2}}\,}$

LA CISOIDE DE DIOCLES, LA DUPLICACIÓN DEL CUBO Y EL PROBLEMA DE DELIAN

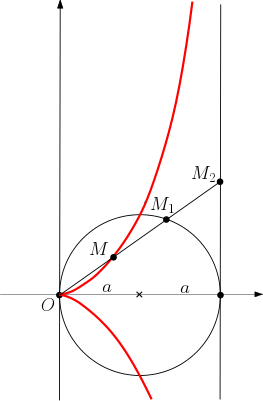
A veces, una curva “clásica” lleva detrás una historia curiosa. Un buen ejemplo de esto es la cisoide de Diocles, una curva plana que se define de la siguiente forma:

Supongamos que tenemos una circunferencia S1(C,a) de centro C=(a,0) y radio a>0 en R2. Dado θ∈(−π/2,π/2), el rayo Rθ={reiθ | r>0} que parte del origen O=(0,0) con ángulo en polares θ, corta a S1(C,a) en un punto M1 y a la recta L={x=2a} en otro punto M2. La cisoide de Diocles es la curva plana θ∈(−π/2,π/2)↦M(θ)∈R2 definida por la condición

∥OM∥=∥M1M2∥.

(en rojo en la siguiente figura)

1. Prueba que en coordenadas polares, M(θ) viene dada por
   
   M(θ)=2asinθtanθeiθ,θ∈(−π/2,π/2).
   
   ¿Es la cisoide una curva regular?
2. Tras hacer el cambio de variable t=tan(θ), demuestra que obtenemos la reparametrización
   
   α(t)=(2at21+t2,2at31+t2),t∈R.
3. Llamando (x,y) a las coordenadas cartesianas de R2, prueba que la ecuación en implícitas de la cisoide de Diocles es
   
   (x2+y2)x=2ay2.
   
   Por lo tanto, la cisoide es el conjunto de ceros del polinomio de orden tres p(x,y)=(x2+y2)x−2ay2, es decir, es una curva algebraica de grado tres, o cúbica (recuerda que las cónicas en el plano viene dadas por ecuaciones de segundo grado en dos variables).

Y ahora, la historia ‘curiosa’ de la cisoide de Diocles: Según el historiador griego Plutarco, los habitantes de la ciudad griega de Atenas sufríeron una epidemia de peste allá por el 429 a.C. Como adoraban al dios Apolo y éste era patrón de la ciudad de Delfos,
algunos atenienses fueron a Delfos a consultar a un oráculo de este dios griego sobre cómo podrían detener la epidemia.  El oráculo les respondió que debían sustituir el altar a Apolo por otro del doble de volumen (desde luego, una respuesta de dudosa utilidad). El altar era cúbico, y los griegos eran muy aficionados a la geometría. Así que se planteó el dilema de cómo calcular el lado u>0 de un cubo de volumen doble de otro cubo dado, de lado a>0. Este problema se conoce como la duplicación del cubo. Evidentemente, la ecuación a resolver era

u3=2a3,

siendo a conocido y u incógnita. Nosotros sabemos despejar u en esa ecuación, pero lo que los griegos querían no era despejarla sino construir el nuevo altar. Así que, sin saberlo, buscaban un método para construir 2–√3, sólo usando regla y compás. Desafortunadamente, este número irracional no es constructible con regla y compás, como demostró Pierre Wantzel (¡ en 1837 !). Pero esto no lo sabían los griegos, por supuesto. Así que empezaron a investigar sobre el tema.

El primer avance significativo sobre este problema lo hizo el geómetra griego Hipócrates de Quíos, que lo redujo al llamado
problema de Delian: dados a,b>0, supongamos que podemos construir u,v>0 tales que

(1)ua=vu=bv.

Hipócrates de Quios se dio cuenta de si suponemos u,v construídos cumpliendo (1), entonces

u3=a3(ua)3=a3uavubv=a3ba=a2b.

Luego tomando b=2a tendremos u3=2a3, y ya está nuestro cubo duplicado.
Desde luego, no parece que hayamos avanzado mucho en nuestro intento de duplicar el cubo: ahora debemos resolver el problema de Delian dados a,b, pero… ¿cómo?

El geómetra (también griego, cómo no) Diocles estudió la cisoide en el siglo II a.C. (no sabemos si la descubrió él, pero lleva su nombre desde entonces) y la usó para resolver el problema de Delian y por tanto la duplicación del cubo. Es decir, si tenemos ya construída la cisoide, entonces Diocles dio un proceso basado en regla y compás para resolver el problema de Delian (por supuesto, de aquí podemos deducir que la cisoide no es constructible con regla y compás,
o al menos no es posible construir todos sus puntos, porque cualquier cantidad finita de ellos sí que puede construírse
por el procedimiento de arriba).

Veamos el método, muy ingenioso, dado por Diocles: Nos dan a,b>0, y queremos construir u,v>0 cumpliendo (1).
Basta construir sólo u>0 tal que

(2)u3=a2b,

porque definiendo v=u2a (recordemos que el producto y cociente de números constructibles con regla y compás sigue siendo constructible) tendremos también construído v, y es fácil probar que estos u,v
resuelven el problema de Delian para a,b.

Así que nos toca construir u>0 tal que (2) se cumple, dados a,b. Para ello, Diocles partió de una cisoide como la que aparece arriba. Llamamos C=(a,0) al centro de la circunferencia de la figura de arriba, y LC={x=a} a la recta vertical que pasa por C. Llevamos la distancia b sobre esta recta LC, empezando en C y en sentido ascendente. De esta forma producimos un punto B=(a,b). Unimos B con A=(2a,0) y llamamos P=(x,y) al punto de corte del segmento AB con la cisoide. Ahora trazamos el segmento OP, que cortará a LC en un punto U=(a,u) para cierto u>0. Y éste es el u que buscamos: como los triángulos OCU y OP0P son semejantes, el teorema de Thales nos dice que

(3)ua=∥CU∥∥OC∥=∥P0P∥∥OP0∥=yx.

Análogamente, la semejanza de los triángulos APP0 y ABC nos lleva a que

(4)y2a−x=∥PP0∥∥P0A∥=∥BC∥∥CA∥=ba.

Por tanto,

u3a3=(3)y3x3=y2yx3=(⋆)x32a−xyx3=y2a−x=(4)ba,

donde en (⋆) hemos usado la ecuación en implícitas de la cisoide. De lo anterior deducimos que u3=a2b como queríamos.