GEOMETRÍA

FIGURAS GEOMÉTRICAS - CURVAS

Arco capaz de ángulo ${\displaystyle \gamma }$ del segmento AB.

El arco capaz es el lugar geométrico de los puntos desde los que un segmento AB se «ve» con el mismo ángulo, es decir, el lugar geométrico de los vértices P de los ángulos APB que tienen la misma amplitud.

El arco capaz de ángulo ${\displaystyle \gamma }$ de un segmento AB es el lugar geométrico de los puntos P tales que ${\displaystyle \angle APB=\gamma }$ y son exclusivamente dos arcos de circunferencia, uno a cada lado del segmento AB, ambos puntos se incluyen uniendo dichos arcos.

mostrar${\displaystyle 2\gamma =\angle ACB}$

Arco capaz del ángulo de 90º

El arco capaz con ángulo ${\displaystyle \gamma }$ = 90º corresponde con el 2º teorema de Tales, de tal modo que el arco capaz es la circunferencia cuyo diámetro es el segmento AB.

Construcción del arco capaz[editar]

Construcción del arco capaz respecto del segmento AB, de ángulo ${\displaystyle \gamma .}$

Para construir el arco capaz de ángulo ${\displaystyle \gamma }$ del segmento AB, en delineación, se empieza por la construcción de la mediatriz del segmento AB que es donde están los posibles centros C del arco capaz.

Primera alternativa

Se construye el ángulo ${\displaystyle \gamma }$ en el punto A sobre el segmento AB, y luego con una escuadra se traza una perpendicular por A al nuevo lado del ángulo que incide en el punto C sobre la mediatriz.

Segunda alternativa

Se construye el ángulo ${\displaystyle \gamma }$ en cualquier punto de la mediatriz, y mediante una paralela al nuevo lado del ángulo que pase por el punto A, se obtiene el punto C sobre la mediatriz.

El arco capaz es el lugar geométrico de los puntos del plano que unidos con los extremos de un segmento AB forman siempre, desde cada uno de esos puntos, un mismo ángulo.

El segundo teorema de Tales es un caso particular del arco capaz, en el que el segmento AB es a la vez diámetro e hipotenusa, mientras que el ángulo constante es de 90°.

Construcción geométrica de un arco capaz

Los datos iniciales son el segmento AB y el valor del ángulo constante α.

Se siguen los siguientes pasos:

1. Con un compás se trazan, desde A y B dos arcos por cuya intersección pasa la mediatriz del segmento AB. Trazar la mediatriz de AB.
2. Desde el extremo A se dibuja la recta que forma un ángulo α con AB.
3. Desde A se traza la perpendicular a la última recta dibujada. Esta perpendicular cortará a la mediatriz en el punto O.
4. El punto O es el centro del arco capaz, desde el que se traza el arco de circunferencia que parte desde A a B, con radio OA.

Todos los puntos del arco capaz “ven” al segmento AB con el mismo ángulo α.

El arco capaz tiene la propiedad de que su centro O está unido con los extremos A y B del segmento con sendos radios OA y OB que forman un ángulo 2α.

Resolución geométrica de triángulos, conociendo la base, la altura y el ángulo superior

ANUNCIOS

Se resuelve geométricamente trazando el arco capaz correspondiente a partir del segmento de la base y del ángulo superior. Veámoslo con un ejercicio.

Ejercicio

Hallar los elementos restantes de un triángulo del que se sabe que la base AB mide 5 cm, su ángulo opuesto C = 30° y la altura sobre esta base 7 cm.

Solución:

Por procedimiento geométrico, se traza el arco capaz correspondiente a ese segmento AB de la base de 5 cm y a un ángulo de 30°.

Se traza una línea paralela a la base separada de ella los 7 cm de la altura del triángulo.

Los dos puntos (C y C’) en que intersecta la paralela al arco capaz serán los dos vértices de los dos triángulossimétricos ΔABC y ΔABC’ que cumplen las condiciones del ejercicio. Veámoslo en el dibujo.

Con instrumentos geométricos, como transportador de ángulos y regla graduada, obtenemos que el ángulo obtuso mide 103,7° y el agudo, 46,3°, mientras que el lado mayor mide 9,7 cm y el menor, 7,2 cm.

Finalmente, el área la obtenemos por la fórmula básica del área del triángulo:

Se obtiene que el área es de 12,5 cm².

https://www.universoformulas.com

centro de curvatura de una curva en un punto dado es el centro del círculo osculador. La distancia entre el centro de curvatura y la propia curva se denomina radio de curvatura. Si la curvatura de la curva, que es la inversa del radio de curvatura, es cero, su centro de curvatura es el punto del infinito.

Por ejemplo si tomamos en cuenta una circunferencia: el centro de la circunsferencia es el "centro de curvatura" y la distancia (constante) de ese centro a cualquier punto de la circunferencia, es el radio (r). También existe la posibilidad de conocer el centro de curvatura de cada punto de una curva diferente a una circunferencia (por ejemplo, de una parábola, de una hipérbola, o de cualquier función). Esto se hace mediante la aplicación de la primera y segunda derivadas de la función en ese punto, y se calcula:

1. Derivar la función en ese punto (es decir y' o la pendiente o tangente en ese punto).
2. Obtener la normal en ese punto (es decir, la perpendicular a la tangente) N=-(1/Tan) o N=-(1/y')
3. Obtener la segunda derivada (y")
4. Obtener el Radio de curvatura mediante la fórmula r= (1+(y')^2) ^(3/2) todo / (y")^2.
5. Conociendo la normal y el radio, se analiza la nueva función (es una recta que se forma sobre la normal). Esto nos permitirá hallar la ubicación del centro de curvatura para ese punto en particular razonando por Pitágotas: Hallaremos su ubicación (x; y) haciendo las diferencias con la posición del punto analizado (x0; y0). Delta x (Diferencia de x-x0)=r/ (Raíz de ((Normal ^2 +1)) y Delta y=Raíz de (r^2-(delta x)^2).

La función que se puede formar uniendo todos los centros de curvatura de la función inicial se llama evoluta.

 circunferencia es una curva plana y cerrada tal que todos sus puntos están a igual distancia del centro.¹​

Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan a otro punto llamado centro.

Distíngase de círculo, cuyo lugar geométrico que queda determinado por una circunferencia y la región del plano que encierra esta.

El interés por conocer la longitud de una circunferencia surge en Babilonia. Cuando usaban los carros con ruedas, era primordial relacionar el diámetro o radio con la circunferencia.²​

Terminología frecuente[editar]

Elementos relevantes de la circunferencia, heredados por el círculo:

• El centro es el punto equidistante a todos los puntos de una circunferencia. Señalado con el nombre ${\displaystyle C}$ en la figura.
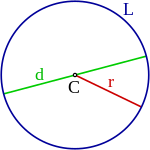
• Un radio es cualquier segmento que une el centro de la circunferencia con un punto cualquiera de la misma. El radio también es la longitud de los segmentos del mismo nombre. Señalado con el nombre ${\displaystyle r}$ en la figura.
• Un diámetro es cualquier segmento que une dos puntos de la circunferencia pasando por su centro. El diámetro también es la longitud de los segmento del mismo nombre. Señalado con el nombre ${\displaystyle d}$ en la figura.
• El perímetro es el contorno de la circunferencia y su longitud. Señalado con el nombre ${\displaystyle L}$ en la figura.
  
• Una cuerda es cualquier segmento que une dos puntos de una circunferencia. El diámetro es un cuerda de máxima longitud. Segmento verde en la figura.
• Un arco es cualquier porción de circunferencia delimitada por dos puntos sobre esta. Se dice también que una cuerda subtiende cada arco que determinan sus extremos. Línea curva azul en la figura.
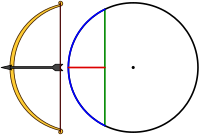
• Una flecha o sagita respecto una cuerda es el segmento de su mediatriz que hay entre esta cuerda y el arco que determina esta, sin pasar por el centro. Segmento rojo en la figura.
• Una semicircunferencia es cualquier arco delimitado por los extremos de un diámetro.

Perímetro[editar]

La longitud de una circunferencia en función del radio ${\displaystyle r}$ o del diámetro ${\displaystyle d=2\cdot r}$ es:

${\displaystyle \ell =2\pi \cdot r=}$ ${\displaystyle \pi \cdot d}$

donde ${\displaystyle \pi =3,14159\dots }$ es la constante pi.

Área[editar]

Artículo principal: Círculo

El área del círculo o de la región del plano delimitada por una circunferencia:

A =${\displaystyle {\frac {\ell \cdot r}{2}}=}$ ${\displaystyle \pi \cdot r^{2}=}$ ${\displaystyle {\frac {\pi \cdot d^{2}}{4}}}$

Propiedades[editar]

mostrarSolo las rectas que contengan el centro de la circunferencia pueden ser un eje de simetría de esta.

mostrarLas circunferencias son invariantes a cualquier rotación con el eje en el centro de esta circunferencia.

Posiciones relativas respecto la circunferencia[editar]

Véase también: Posiciones relativas en el círculo

Los puntos[editar]

Posiciones de los puntos respecto de la circunferencia:

• Un punto exterior es el que está a una distancia mayor al radio de la circunferencia respecto la posición de su centro.
• Un punto interior es el que está a una distancia menor al radio de la circunferencia respecto la posición de su centro.

Las rectas[editar]

Posiciones de las rectas respecto de la circunferencia:

• Una recta exterior es cualquier recta que no tiene puntos en común con la circunferencia.
• Una recta tangente es cualquier recta que toca la circunferencia en un único punto.
• Una recta secante es cualquier recta que corta la circunferencia en dos puntos.³​

Se llama punto de tangencia cada uno de los puntos que comparte la circunferencia con los diferentes elementos tangentes, es decir, el punto donde se produce la tangencia. En todo punto de la circunferencia se pueden hacer tangencias.

Propiedades[editar]

mostrarToda recta tangente a una circunferencia es perpendicular al radio que contiene el punto de tangencia.

Entre circunferencias[editar]

Posiciones entre circunferencias:

• Una circunferencia es exterior a otra, si todos sus puntos son exteriores a esta otra. Véase la figura 1 y 8.
• Una circunferencia es interior a otra, si todos sus puntos son interiores a esta otra. Véase la figura 5.
• Una circunferencia es circundante a otra, si todos sus puntos no son interiores a esta otra que a su vez no es exterior a la primera. Véase las figuras 7 y 8.
• Una circunferencia es tangente exterior a otra, si tienen un único punto común y todos los demás puntos de una son exteriores a la otra. Véase la figura 2.
• Una circunferencia circundante es tangente exterior a otra, si tienen un único punto común. Véase la figura 7.
• Una circunferencia es tangente interior a otra, si tienen un único punto común y todos los demás puntos de una son interiores a la otra. Véase la figura 4.
• Una circunferencia es secante a otra, si se cortan en dos puntos distintos. Véase la figura 3.
• Una circunferencia es secante ortogonalmente a otra, si el ángulo de su intersección es recto, es decir, sus rectas tangentes en cada una de las intersecciones son perpendiculares.
• Son excéntricas las circunferencias que no tienen el mismo centro.
• Son concéntricas las circunferencias que tienen el mismo centro, es decir, las que no son excéntricas.
• Son coincidentes las circunferencias que tienen el mismo centro y el mismo radio, es decir, que todos los puntos de una son los de la otra y viceversa. Véase la figura 6.

Propiedades[editar]

mostrarLos centros de las circunferencias tangentes están alineados con el punto de tangencia.

Ángulos en una circunferencia[editar]

Posición de los ángulos respecto de una circunferencia, puede ser:

• Un ángulo central es el que tiene su vértice en el centro de la circunferencia.⁴​ Véase la figura 1.
• Un ángulo inscrito es el que tiene su vértice sobre la circunferencia cuyos lados determinan una cuerdas cada uno en la dicha circunferencia.⁴​ Véase la figura 2.
• Un ángulo semi-inscrito es el que tiene su vértice sobre la circunferencia y uno de sus lados secantes determina una cuerda y el otro una recta tangente a la circunferencia, es decir, que el vértice es un punto de tangencia.⁴​ Véase la figura 3.
• Un ángulo ex-inscrito es el que tiene su vértice sobre la circunferencia y uno de sus lados determina una cuerda y la prolongación del otro determina otra cuerda, es decir, es el ángulo exterior de un ángulo inscrito.⁵​ Véase la figura 4.
• Un ángulo interior es el que tiene su vértice en el interior de la circunferencia.⁴​ Véase la figura 5.
• Un ángulo exterior es el que tiene su vértice en el exterior de la circunferencia y cada lado es tangente o secante a la circunferencia.⁴​ Véanse las figuras 6,7 y 8.

Propiedades[editar]

En el ángulo central su amplitud ${\displaystyle \alpha }$ y el radio ${\displaystyle r}$ de la circunferencia, determina la longitud del arco ${\displaystyle \ell ,}$ resaltado en la figura en azul. Si el ángulo está en grados:

mostrar${\displaystyle \ell _{\alpha }=}$ ${\displaystyle {\frac {\alpha }{180^{\circ }}}\cdot \pi \cdot r}$

Si el ángulo está en radianes:

${\displaystyle \ell _{\alpha }=}$ ${\displaystyle \alpha \cdot r}$

Artículo principal: Arco capaz

El arco capaz relaciona el ángulo central, inscrito, semi-inscrito y ex-inscrito siempre que las intersecciones de los lados mantengan la misma distancia.

Si el ángulo inscrito, semi-inscrito y ex-inscrito tienen la misma amplitud ${\displaystyle \alpha }$, entonces, determinan la misma longitud de arco, de color azul en la imagen, sobre una misma circunferencia de radio ${\displaystyle r}$. Si el ángulo está en grados:

mostrar${\displaystyle \ell _{\alpha }=}$ ${\displaystyle {\frac {\alpha }{90^{\circ }}}\cdot \pi \cdot r}$

Si el ángulo está en radianes:

${\displaystyle \ell _{\alpha }=}$ ${\displaystyle \alpha \cdot 2\cdot r}$

Diversos tipos de ángulos aparecen en el análisis de la potencia de un punto respecto de una circunferencia.

Inscripción y circunscripción[editar]

Diremos que una circunferencia está circunscrita a un polígono cuando todos los vértices de dicho polígono están sobre esta, se dice que este polígono está inscrito.

Diremos que una circunferencia está inscrita a un polígono cuando sea tangente a todos los lados de dicho polígono, se dice que este polígono está circunscrito.

Representación de la circunferencia[editar]

La circunferencia se puede representar mediante ecuaciones o funciones que determinan la posición de cada uno de sus puntos. Para ello solo hace falta garantizar que la distancia de cada punto ${\displaystyle P}$ de la circunferencia a su centro ${\displaystyle C}$ sea constante para cada una de las ecuaciones y funciones que se tenga.

Ecuación de la circunferencia[editar]

circunferencia de radio dos en un sistema de coordenadas

Una circunferencia queda determinada por un centro ${\displaystyle C=(a,\,b)}$ y un radio ${\displaystyle r}$, por tanto, su ecuación queda determinada al imponer que la distancia de sus puntos, ${\displaystyle P=(x,\,y)}$, al centro sea constante, es decir, ${\displaystyle \|P-C\|=r}$ dando la siguiente ecuación:⁶​⁷​

${\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}.}$

Su representación en un sistema de coordenadas viene dada por cada punto de la forma ${\displaystyle (x,\,y)}$ que satisfacen la ecuación.

La ecuación anterior es más sencilla si está centrada en el origen de coordenadas ${\displaystyle C=(0,\,0):}$

${\displaystyle x^{2}+y^{2}=r^{2}.}$

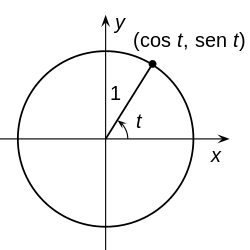
La circunferencia de centro en el origen de coordenadas y radio uno se denomina circunferencia unidad o circunferencia goniométrica y su ecuación es:⁸​⁹​¹⁰​¹¹​¹²​

${\displaystyle x^{2}+y^{2}=1.}$

Su función implícita es ${\displaystyle f(x,\,y)=x^{2}+y^{2}-1}$ y para representar la circunferencia se buscan los puntos del plano que cumplen la ecuación ${\displaystyle f(x,\,y)=0.}$

Propiedades[editar]

• Es posible usar cuadratura para hallar la ecuación de la circunferencia a partir de su ecuación extendida:

mostrar${\displaystyle x^{2}+y^{2}+Dx+Ey+F=0}$

• A partir de los puntos extremos de un diámetro, ${\displaystyle (x_{1},y_{1})}$ y ${\displaystyle (x_{2},y_{2})}$, la ecuación de la circunferencia es:

mostrar${\displaystyle (x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0.}$

Función paramétrica[editar]

La circunferencia con centro en ${\displaystyle C=(a,\,b)}$ y radio ${\displaystyle r}$ se puede parametrizar usando funciones trigonométricas de un solo parámetro ${\displaystyle \theta }$ para obtener una función paramétrica ${\displaystyle r_{C}(\theta )=(x,\,y):}$

${\displaystyle {\begin{array}{l}x=a+r\,\cos \theta \\y=b+r\,\operatorname {sen} \theta \end{array}}}$ ${\displaystyle \theta \in [0,\,2\,\pi )}$

También se puede parametrizar con funciones funciones racionales como

mostrar${\displaystyle {\begin{array}{l}x=a+r\left({\frac {1-t^{2}}{1+t^{2}}}\right)\\y=b+r\left({\frac {2t}{1+t^{2}}}\right)\end{array}}}$ ${\displaystyle t\in {\bar {\mathbb {R} }}}$

donde ${\displaystyle {\bar {\mathbb {R} }}}$ incluye el punto en el infinito.¹³​

Función paramétrica en el plano complejo[editar]

En el plano complejo, una circunferencia con centro ${\displaystyle C=a+i\,b}$ y radio ${\displaystyle r}$ a partir de la ecuación de la circunferencia ${\displaystyle |z-c|=r}$ se obtiene la forma paramétrica:¹⁴​¹⁵​

${\displaystyle z=re^{i\theta }+C=}$ ${\displaystyle r(\cos \theta +i\operatorname {sen} \theta )+a+i\,b}$

donde ${\displaystyle \theta \in [0,\,2\,\pi ).}$

Función vectorial[editar]

Como en la función paramétrica, la circunferencia puede representarse en cualquier subespacio de dimensión dos de un espacio vectorial usando dos vectores ortonormales ${\displaystyle {\vec {u}}}$ y ${\displaystyle {\vec {v}}}$, y por tanto generadores de dicho subespacio, permitiendo construir la circunferencia en cualquier plano oblicuo con centro ${\displaystyle {\vec {c}}}$ y radio ${\displaystyle r}$ que viene dada o descrita por la función vectorial:

${\displaystyle r(\theta )=}$ ${\displaystyle {\vec {c}}+{\vec {u}}r\cos \theta +{\vec {v}}r\operatorname {sen} \theta }$ donde ${\displaystyle \theta \in [0,\,2\pi ).}$

Ecuación en coordenadas polares[editar]

Circunferencia unitaria.

Toda curva plana dada en coordenadas polares es de la forma ${\displaystyle \alpha (\theta )=}$ ${\displaystyle (\rho (\theta )\cos \theta ,\,\rho (\theta )\operatorname {sen} \theta )}$ donde ${\displaystyle \rho (\theta )}$ es la distancia al centro o polo ${\displaystyle O}$ y ${\displaystyle \theta }$ el ángulo respecto el eje OX, por tanto la expresión de una circunferencia con centro en el polo y radio ${\displaystyle r}$ es:

mostrar${\displaystyle \alpha (\theta )=}$ ${\displaystyle (r\cos \theta ,\,r\operatorname {sen} \theta )}$

Cuando el centro está en el punto ${\displaystyle (d,0)}$ con radio ${\displaystyle r}$ la circunferencia es:

mostrar${\displaystyle \alpha (\theta )=}$ ${\displaystyle (\rho (\theta )\cos \theta ,\,\rho (\theta )\operatorname {sen} \theta )}$ donde ${\displaystyle \rho (\theta )=}$ ${\displaystyle d\cos \theta +{\sqrt {r^{2}-d^{2}\operatorname {sen} \theta }}}$

Propiedad[editar]

• Dados tres puntos cualesquiera no alineados ${\displaystyle (x_{1},\,y_{1}),\,(x_{2},\,y_{2})}$ y ${\displaystyle (x_{3},\,y_{3})}$ existe una única circunferencia que contiene a estos tres puntos, es decir, esta circunferencia estará circunscrita al triángulo definido por estos puntos. La ecuación de la circunferencia está dada de por el determinante matricial:

${\displaystyle \det {\begin{bmatrix}x&y&x^{2}+y^{2}&1\\x_{1}&y_{1}&x_{1}^{2}+y_{1}^{2}&1\\x_{2}&y_{2}&x_{2}^{2}+y_{2}^{2}&1\\x_{3}&y_{3}&x_{3}^{2}+y_{3}^{2}&1\\\end{bmatrix}}=0.}$

Formas de identificar circunferencias[editar]

Según el área que se trabaje, hay formas de identificar y usar una circunferencia implícitamente, además de sus funciones y ecuaciones.

En topología[editar]

En topología, se denomina circunferencia a cualquier curva cerrada simple que sea homeomorfa a la circunferencia usual de la geometría (es decir, la esfera 1–dimensional). Se la puede definir como el espacio cociente determinado al identificar como uno los dos extremos de un intervalo cerrado. Sin embargo, los geómetras llaman 2-esfera a la circunferencia, mientras que los topólogos se refieren a ella como 1-esfera y la indican como ${\displaystyle S^{1}\,\!}$, dando lugar a posibles confusiones.¹⁶​

La dimensión de la circunferencia es 1. De igual modo, la dimensión de una recta no acotada, o de un arco — esto es de un conjunto homeomorfo con un intervalo cerrado — y de una curva cerrada simple, i.e. un conjunto homeomorfo con una circunferencia, es igual a 1.¹⁷​ También el caso de una poligonal cerrada.

En ecuaciones diferenciales[editar]

En el tema de ecuaciones diferenciales, una circunferencia puede determinarse mediante una curva integral de una ecuación diferencial como:

${\displaystyle {\begin{array}{l}x'=-y\\y'=\,x\end{array}}}$

En geometría diferencial de curvas[editar]

En teoría local de la curva, se considera como circunferencia una curva de curvatura constante sin torsión.

Circunferencias particulares[editar]

Circunferencias de Cardanus[editar]

Un par de circunferencias que se desplazan, tangencial e interiormente, una sobre la otra guardando una razón entre sus radios de 1:2. Investigadas, originalmente, por el matemático italiano, Girolamo de Cardano¹⁸​

Circunferencia directriz[editar]

Usada en una alternativa definitoria de la elipse y de la hipérbola. Siendo estas el lugar de los centros de las circunferencias tangentes a la llamada circunferencia directriz.¹⁸​

Circunferencia osculatriz[editar]

Al tratar de la curvatura de una curva o de una superficie, en el punto de contacto, además de la tangente se toma en cuenta la circunferencia de la curvatura, llamada circunferencia osculatriz