AMIGOS PARA SIEMPRE: ÓPTICA

FENÓMENOS ÓPTICOS

difracción es un fenómeno característico de las ondas que se basa en la desviación de estas al encontrar un obstáculo o al atravesar una rendija. La difracción ocurre en todo tipo de ondas, desde ondas sonoras, ondas en la superficie de un fluido y ondas electromagnéticas como la luz visible y las ondas de radio. También sucede cuando un grupo de ondas de tamaño finito se propaga; por ejemplo, por causa de la difracción, el haz colimado de ondas de luz de un láser debe finalmente divergir en un rayo más amplio a una cierta distancia del emisor.

Esquema de una onda de longitud de onda

λ

difractada por dos rendijas separadas una distancia d, en el dibujo se muestran los ordenes de difracción m.

Teoría[editar]

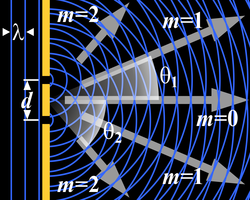
La difracción puede ser entendida a nivel fenomenológico usando el principio de Huygens, según el cual un frente de onda se puede visualizar como una sucesión de emisores puntuales, que reemiten la onda al oscilar, en respuesta a ella y contribuyen así a su propagación. Aunque cada oscilador individual genera una onda esférica, la interferencia de todas ellas da lugar a una onda plana que viaja en la misma dirección que la onda inicial. Cuando el frente de onda encuentra un obstáculo los emisores correspondientes al extremo del frente de onda obstruido no tienen otros emisores que interfieran con las ondas que ellos generan, y estas se aproximan a ondas esféricas o cilíndricas. Como consecuencia, al adoptar el frente de onda una forma redondeada en donde fue recortado, la dirección de propagación de la onda cambia, girando hacia el obstáculo. Se suele decir que la onda "dobla" las esquinas.

Los efectos de la difracción pueden predecirse matemáticamente usando dos aproximaciones distintas. La difracción de Fraunhofer permite estimar el comportamiento del fenómeno producido por un obstáculo situado a una distancia lo suficientemente alejada de la zona de estudio. Es un método matemáticamente sencillo, pero limitado por dicha condición. Por otro lado, la aproximación conocida como difracción de Fresnel toma en cuenta el carácter vectorial de las elongaciones de las ondas, permitiendo realizar predicciones en las cercanías del obstáculo que produce la difracción. Es matemáticamente más complicada que el método de Fraunhofer, por lo que su aplicación se limita solo a las regiones donde la difracción de Fraunhofer no es aplicable.

Resulta interesante pensar a la difracción como una consecuencia de la ecuación de onda. Mientras que una onda plana infinita es solución de la ecuación de onda, una onda plana recortada no lo es. Para que la misma sea una solución de dicha ecuación debe introducirse la difracción. Es el caso de un rayo láser que es una onda plana pero obstruida por las dimensiones finitas del dispositivo de generación. La consecuencia inmediata es que la ecuación de onda exige que dicha condición no persista y se introduce inmediatamente una componente de difracción. Por eso el haz diverge a medida que avanza, incrementándose su sección.

Cabe mencionar que la difracción es una de los cinco fenómenos de la luz en la que se encuentran la Reflexión, refracción, interferencia y polarización.

Difracción e interferencia[editar]

La difracción y la interferencia son fenómenos inseparables, al punto que no es siempre sencillo distinguirlos. Esto es debido a que la difracción es una forma particular de interferencia. Citando a Richard Feynman¹, con una traducción libre:

«Nadie ha sido capaz de definir la diferencia entre interferencia y difracción de forma satisfactoria. Es solo una cuestión de uso, sin diferencias físicas importantes».

Como consecuencia, cuando en la física, se necesita estudiar formas de interferencia específicas, es necesario poder distinguir los efectos provenientes de las mismas a los efectos provenientes de la difracción.

La interferencia se produce cuando la longitud de onda

λ

es mayor que las dimensiones del objeto, por tanto, los efectos de la difracción disminuyen hasta hacerse indetectables a medida que el tamaño del objeto aumenta comparado con la longitud de onda.

Aplicaciones[editar]

Para microscopistas y fotógrafos la difracción, por lo general, una limitante para obtener imágenes nítidas. Sin embargo, el efecto se puede aprovechar para varias técnicas.

Mencionamos tres aplicaciones de la difracción: 1) experimentos para demostrar la dualidad onda-partícula, 2) análisis de patrones de difracción para conocer la estructura de materiales cristalinos y 3) el uso de redes de difracción para construir espectrómetros, instrumentos que permiten identificar sustancias en materiales.

Debido a la dualidad onda-corpúsculo característica de la mecánica cuántica es posible observar la difracción de partículas como neutrones o electrones. En los inicios de la mecánica cuántica este fue uno de los argumentos más claros a favor de la descripción ondulatoria que realiza la mecánica cuántica de las partículas subatómicas.

Instrumento didáctico para estudiar la difracción de electrones de baja energía

En lo respecta al espectro electromagnético, los rayos X presentan longitudes de onda similares a las distancias interatómicas en la materia. Por ello, es posible utilizar la difracción de rayos X como un método para explorar la naturaleza de los cristales y otros materiales con estructura periódica.

Por ejemplo, la difracción de rayos X producida por una estructura cristalina (como de la sal de mesa: NaCl) verifica la ley de Bragg. Analizando la geometría del patrón de difracción se puede inferir la estructura con la que se ordenan las moléculas en la muestra estudiada. Así, esta técnica se utilizó para discernir la estructura del ADN, y fue una de las pruebas fácticas² de su configuración de doble hélice presentadas por James Watson y Francis Crick³ en 1953.

Un patrón de difracción de ADN

En lo que respecta al espectro electromagnético cercano a la región visible, el fenómeno de difracción se aprovecha para estudiar e identificar sustancias por medio de alguna técnica espectroscópica⁴. Por ejemplo, los espectrómetros de absorción óptica suelen mostrar la siguiente instrumentación: una lámpara ilumina una muestra (que puede ser un colorante disuelto en un líquido trasparente); la luz emitida de la muestra cuenta con información sobre la composición y estructura del colorante, y es por medio de una rejilla de difracción que esta luz se descompone (como lo hace un prisma con un rayo de luz, pero de modo más eficiente), dirigiendo la luz hacia un sensor, el cual cuenta con una interface conectada a una computadora. La rejilla de difracción es un componente esencial para construir instrumentos de alta exactitud como lo espectrómetros.