El problema de la cuerda que rodea la Tierra es un acertijo matemático con una solución contraintuitiva. En una versión común del problema, se supone que se enrolla una cuerda alrededor del ecuador de la Tierra, que se considera perfectamente esférica. Esta cuerda se corta y se agrega una pieza de longitud 1 m. La cuerda ahora se ha recolocado para que esté a una altura uniforme sobre el ecuador. La pregunta que se plantea es si la separación entre la cuerda y la Tierra permitirá el paso de un automóvil, de un gato o de la hoja de un cuchillo.
Solución[editar]
Teniendo en cuenta que 1 m es casi despreciable en comparación con los 40.000 km de la circunferencia de la Tierra, la primera impresión lleva a contestar que la nueva posición de la cuerda prácticamente no será diferente de la posición original sobre la superficie. Sorprendentemente, la respuesta correcta es que un gato pasará fácilmente por debajo de la cuerda, cuyo separación del suelo será de 12π metros o aproximadamente 16 cm. Aún más sorprendente es que el tamaño de la esfera o círculo alrededor del cual se extiende la cuerda es irrelevante, y puede ser cualquier cosa desde el tamaño de un átomo hasta el de la Vía Láctea, y el resultado seguirá siendo 16 cm.1
Sea C la circunferencia de la Tierra, R su radio, c la longitud agregada a la cuerda y r el aumento del radio. Como un círculo de radio R tiene una circunferencia de 2πR , entonces:
independientemente del valor de C.
Un corolario es que, para elevar la cuerda original 16 cm del suelo en todo el ecuador, solo se necesita agregar 1 m a la cuerda.
Esto también significa que una pista de atletismo tiene el mismo desplazamiento entre las líneas de inicio en cada calle, igual a 2π el ancho de la calle, tanto como si el perímetro de la pista es de 400 m o tiene el tamaño de la Vía Láctea.
Las matemáticas son maravillosas, y eso es algo que cualquiera que se haya atrevido a mirar más allá de lo que uno puede aprender en la escuela sabe. Hoy quiero mostraros un problema que cualquier persona puede resolver fácilmente sin tener que aprender muchas fórmulas. Este es uno de esos problemas que, dado su carácter tan anti-intuitivo, nos da un resultado difícil de creer pero, después de todo, cierto.
Para comenzar con lo que hoy quiero mostraros vamos a imaginar que cogemos una cuerda y damos la vuelta al mundo. Si, algo que todos hacemos al menos una vez a la semana. La longitud de esta cuerda es el perímetro de la Tierra, que llamaremos P, y que podemos calcular con la fórmula que nos da el perímetro de una esfera:
donde R es el radio de la Tierra. Deberemos suponer que la Tierra es una esfera perfecta.
Ahora imaginemos que añadimos un metro a esa misma cuerda y volvemos a rodear la Tierra. Si, otra vez. Llegados a este punto, cabría preguntarse: “¿Cuánto se ha separado la cuerda de la superficie de la Tierra?”
A priori uno podría pensar que se separa muy poco, pues solo hemos añadido 1 metro a la cuerda, que comparado con los 40.075.000 metros que tiene la Tierra de perímetro es una cantidad casi despreciable.
Lo cierto es que si así fuera, no estaría haciendo este artículo, así que vamos a recurrir a las matemáticas para ver que pasa con esa cuerda. Antes de empezar quiero que apuntéis en un papel cuánto creéis vosotros que se separara, y al final comparéis el resultado.
El problema que se nos plantea es el siguiente:

Ahora lo único que tenemos que hacer es desarrollar la segunda ecuación, sabiendo que la longitud de la segunda cuerda es 1 m más que la longitud de la primera, y que el segundo radio es el primero más la distancia que nosotros queremos hallar. Es decir:

Como ya he dicho antes, la distancia que nosotros queremos hallar es x. Por último, sustituimos ambos resultados en la ecuación y la desarrollamos:

Y ese es nuestro resultado. ¿No resulta extraño? Si comparáis el resultado con el que vosotros habéis escrito en el papel lo más probable es que el que hemos obtenido sea más grande.
Pero hay algo más sorprendente aún, si observamos el resultado vemos que se trata de una cantidad fija y que no depende de ningún parámetro (en este caso el radio). Esto quiere decir que siempre que añadamos un metro a una cuerda, sin importar su longitud, el radio de la circunferencia que esta forma aumentara en casi 16 centímetros.
Lo bueno de este resultado es que ya no necesitamos comprobarlo dando la vuelta a la Tierra, simplemente con una cuerda más pequeña y una pelota bastará.
https://fisicadeunestudiante.wordpress.com/2017/07/06/la-cuerda-que-rodea-la-tierra/
Se denomina duplicación del cubo al problema de hallar, mediante el uso de solo regla y compás, el lado de un cubotal que su volumen sea el doble del volumen de otro cubo de lado dado. Las técnicas del álgebra son capaces de resolver este problema de forma trivial, pero la restricción de regla y compás lo hacen imposible.
En el año 429 a. C., Pericles, gobernador de Atenas por esa época, muere víctima de la tifoidea que plagaba la ciudad. A raíz de este suceso algunos de los habitantes deciden ir a la ciudad de Delfos para hacer consultas al Oráculo de Apolo y saber cómo pueden detener la epidemia. La respuesta a la consulta del Oráculo es que debían elaborar un nuevo altar en forma de cubo cuyo volumen duplique el del altar que ya existe. Lo intentaron, es muy seguro, pero también fue cierto que no lograron evitar el desastre por este medio. La pandemia se disipó con el tiempo, pero el problema matemático planteado permaneció.
Los primeros intentos[editar]
El primero en abordar el problema sin éxito fue el griego Hipócrates de Quíos; encontró que si entre dos segmentos, uno el doble del otro se insertan dos medias proporcionales, se duplicaría el cubo.1 En notación clásica: a:r:: r:s:: s:2a. Basándose en el mismo planteamiento lo intentaron otros matemáticos posteriores, tales como Arquites de Tarento, Menecmo y Eratóstenes de Cirene, pero todos ellos presentan soluciones aproximadas, ninguna de las cuales puede resolver el problema en forma exacta.
La solución[editar]
A partir de los trabajos de Ruffini, Abel y Galois, en el siglo XIX, y en especial del geómetra francés Pierre Wantzel (1837) se demostró que es imposible resolver este problema usando apenas regla y compás.
Introducción:
En este post vamos a presentar los tres problemas mas famosos que más preocuparon a los griegos desde que aquella ciencia empezó a construirse racionalmente. Estos tres problemas son: la duplicación del cubo, la trisección del ángulo y la cuadratura del círculo, que los griegos no supieron resolver, ni nosotros tampoco.
En este post vamos a presentar los tres problemas mas famosos que más preocuparon a los griegos desde que aquella ciencia empezó a construirse racionalmente. Estos tres problemas son: la duplicación del cubo, la trisección del ángulo y la cuadratura del círculo, que los griegos no supieron resolver, ni nosotros tampoco.
La única ventaja que tenemos sobre ellos es la de saber por qué son irresolubles. Como dichos problemas han trastornado a tantas cabezas de aficionados a la Matemática y todavía existe una pintoresca fauna de locos inofensivos que cree haberlos resuelto, conviene precisar lo que quiere decir “resolver un problema” que es, precisamente, lo que no saben los pobres ilusos que se caracterizan tanto por su ignorancia de Matemática actual y de la historia de esta ciencia como la testaruda resistencia pasiva que oponen a todo intento para convencerles de su error.
En primer lugar, decir que un problema es irresoluble no tiene sentido si no se indica con qué medios o instrumentos, porque pudiera ocurrir que un problema que n tiene solución con ciertos recursos, la tenga con otros; y e segundo lugar, hay que distinguir entre la posibilidad y resolubilidad de de un problema: un problema es posible cuando admite una solución, aunque ésta no se pueda obtener por medio de construcciones elementales, de modo que la resolubilidad es un concepto relativo porque, en sentido absoluto, todo problema posible es resoluble.
La resolución de un problema consiste esencialmente en reducirlo a otro ya resuelto, y, por tanto, se debe llegar a uno, considerado como fundamental, cuya solución se supone dada por uno o varios de los postulados que se refieren al uso legítimo de los instrumentos necesarios para ciertas construcciones geométrica que para los griegos .eran la regla y el compás: únicos aparatos de su actividad matemática hasta el punto de que no concedían carta de naturaleza científica a las figuras cuya construcción exige instrumentos distintos de aquéllos.
Con la regla se puede construir la recta que pasa por dos puntos, el punto común a dos rectas no paralelas, y, en general, los problemas de primer grado, es decir: los que, expresados en lenguaje analítico, sólo contienen la primera potencia de la incógnita, y si en el problema entran nociones métricas como las de paralelismo, longitudes de segmentos, valores angulares, etc., es irresoluble con la regla; con el compás es posible describir una circunferencia centro y radio dados, o de centro dado y que pase por punto dado, y determinar los puntos comunes a dos circunferencias secantes, y, por último, con la regla y el compás son resolubles muchísimos problemas siempre que su expresión algebraica sólo contenga raíces cuadradas. Modernamente se ha demostrado que la regla y el compás se pueden sustituir por una regla de bordes paralelos; pero esto no lo sabían los griegos ni lo saben tampoco los actuales cultivadores de la Matemática patológica.
1) Duplicación del Cubo:
El de la duplicación del cubo tiene un origen fabuloso y constituye el tema de una carta de Eratóstenes al rey Ptolomeo, que dice así: “Cuéntase que uno de los antiguos poetas trágicos hacía aparecer en escena a Minos en el momento en que se construía la tumba de Glauco, y, al observar que sólo medía cien pies por cada lado, dijo: “Es un espacio muy pequeño para sepulcro de un rey; duplicadla conservando su forma cúbica, duplicando cada lado”. Es evidente que se equivocaba porque duplicando los lados de una figura plana se cuadruplica, mientras que una sólida se octuplica; y entonces, se propuso a los geómetras la cuestión de duplicar una figura sólida dada conservando su forma, y este problema se llamó duplicación del cubo.
Después de un largo período de incertidumbre, Hipócrates de Quío encontró que si entre dos rectas, una de las cuales es doble de la otra, se insertan dos medias en proporción continua, el cubo quedará doblado, con lo que no hizo sino transformar la dificultad en otra no menor. Se cuenta también que, más tarde, los de Delos, obligados por el oráculo a duplicar el altar, tropezaron con la misma dificultad y entonces enviaron embajadores a los geómetras que, con Platón, frecuentaban la Academia, para que resolvieran la cuestión.
Se ocuparon de ella diligentemente y se dice que, al proponerse insertar dos medias entre dos rectas, lo consiguieron Arquitas de Tarento con el semicírculo y Eudoxio mediante ciertas curvas. A estos siguieron otros que se esforzaron por hacer más perfectas las demostraciones; pero no pudieron efectuar la construcción y acomodarla a la práctica, excepto, acaso, Menecmo, y cón gran trabajo”.
En este importante documento hist6rico, Eratóstenes se hace eco de dos fábulas: una toma como punto de partida la escena en que Eurípides hace cometer al legendario rey de Creta, ante la tumba de su hijo, el error de decir que duplicando la arista de un cubo se duplica su volumen, error que corrige Eratóstenes haciendo observar que duplicando los lados de una “figura plana” —el cuadrado— se cuadruplica [su área] (fig. 13) y haciendo lo mismo con una “sólida” —el cubo (fig. 14) se octuplica [su volumen]; y la otra leyenda alude a la orden de la pitonisa de Delos de duplicar el altar dedicado a Apolo para aplacar la ira de los dioses que habían desencadenado una epidemia en la isla.
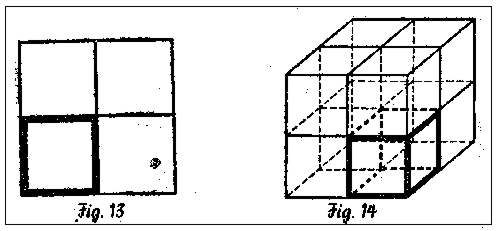
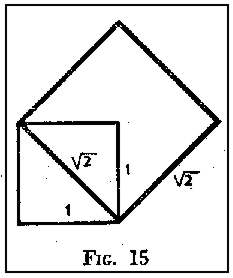
Es probable que el problema de duplicar el cubo, también llamado problema de Delos o problema délico, no fuera inspirado por la megalomanía de Minos ni por el oráculo de la sibila, sino por los propios geómetras puesto que sabiendo desde los tiempos de Pitágoras que el cuadrado construido sobre la diagonal de otro tiene doble área que éste (fig. 15), es decir: sabiendo duplicar el cuadrado mediante la construcción gráfica de la raíz cuadrada de 2 y guiados por su espíritu de generalización, parece natural que quisieran trasportar al espacio el mismo problema, lo que les llevó al de extraer la raíz cúbica de 2, y ante la imposibilidad de construir con la regla y el compás la arista de un cubo de doble volumen que otro, redujeron el problema a otro y, según Eratóstenes, fue Hipócrates de Quío el primero que lo intentó.
Este geómetra —a quien no hay que confundir con su homónimo y contemporáneo el de Cos, padre de la Medicina— nació hacia 450 antes de C. y fue comerciante hasta que los recaudadores de la Aduana ateniense que residían en el Quersoneso lo despojaron de sus bienes y, para reclamar los, se trasladó a Atenas, cuyos ciudadanos se burlaron de él por la ingenuidad que suponía en un extranjero creer que se le iba a hacer justicia. Otros historiadores opinan que la, presencia de Hipócrates en la capital del Ática obedeció al intento de recuperar. las mercancías de uno de sus barcos apresados por piratas atenienses en las proximidades de Bizancio, lo cual era también una tontería.
Sea de ello lo que fuere, es lo cierto que Hipócrates aparece en Atenas por los años de 430, y mientras gestionaba la reivindicación de sus derechos —en lo que están de acuerdo todos los eruditos, ya que no en la causa de la reivindicación— asistió a las lecciones de los filósofos y abrió una escuela de Geometría que fue la que echó las bases del método de reducción que, como hemos dicho antes, consiste en trasformar un problema en otro ya resuelto.
Es posible que tal procedimiento, que parece inseparable de la investigación matemática, hubiera sido empleado antes de Hipócrates, pero fue éste quien descubrió d trato lógico común a muchos métodos para resolver problemas y demostrar teoremas y quien lo aplicó cuestiones.
Conclusión:
Los problemas de duplicar el cubo y trisecar el ángulo, son problemas irracionales, es decir problemas cuyas soluciones son irracionales, y como dependen de ecuaciones de tercer grado no se pueden resolver con a regla y el compás por exigir construcciones en el espacio. La cuadratura del círculo es de otra naturaleza, pues depende del número PI que no puede ser solución de ninguna ecuación de coeficientes enteros, según demostró Lindemann el año 1882, y, por tanto, dicha cuadratura también es imposible con regla y compás.
Los problemas de duplicar el cubo y trisecar el ángulo, son problemas irracionales, es decir problemas cuyas soluciones son irracionales, y como dependen de ecuaciones de tercer grado no se pueden resolver con a regla y el compás por exigir construcciones en el espacio. La cuadratura del círculo es de otra naturaleza, pues depende del número PI que no puede ser solución de ninguna ecuación de coeficientes enteros, según demostró Lindemann el año 1882, y, por tanto, dicha cuadratura también es imposible con regla y compás.
A pesar de que desde el año 1775 la Academia de Ciencias de París tomó el acuerdo —adoptado después por otras— de rechazar las pretendidas soluciones de estos tres problemas, siguen lloviendo sobre las corporaciones, científicas multitud de comunicaciones acerca de los mismos, que, naturalmente, van a parar al cesto de papeles sin ser leídas, y esto —que ya está divulgado hasta la saciedad en libros y revistas— no ha bastado, ni basta, ni bastará para curar la enfermedad que padecen los duplicadores, trisectores y cuadradores, a los que hay que añadir los “demostradores» del Postulado de Euclides, empeñados en no emplear más armas que las de los griegos antiguos porque ignoran la existencia de las bombas atómicas de la Matemática actual que han demostrado la insuficiencia de los primitivos artefactos bélicos.
Ni qué decir tiene que la ignorancia de los duplicadores, trisectores, cuadradores y postuladores, va unida a una insigne pedantería que les inspira un olímpico desdén por quienes les aconsejan honestamente que se enteren de los trabajos hechos por sus predecesores para soslayar el peligro de descubrir Mediterráneos, porque todos ellos excepción— se creen genios desconocidos, y desde luego superiores al medio matemático de su época, y los más enterados se consideran en el caso de un Ruffini, que no con siguió que el Instituto de Francia examinara su demostración de la imposibilidad de resolver por radicales las ecuaciones algebraicas de grado superior al cuarto, o de un Grauss, que no quiso publicar sus investigaciones sobre las Geometrías no-euclídeas por temor al “clamoreo de los beocios”.
https://historiaybiografias.com/problemas_griegos01/
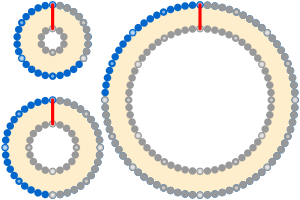



![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
No hay comentarios:
Publicar un comentario