PROBLEMAS MATEMÁTICOS

problema de la galería de arte o problema del museo es un problema de visibilidad muy estudiado en la geometría computacional. La cuestión fue planteada por Victor Klee en 1973 en estos términos: Determinar el mínimo número de puntos de un polígono que son suficientes para ver a todos los restantes. Se puede interpretar también en términos de vigilancia de una sala poligonal.

La motivación de este problema se da por que las Galerías de Arte tienen que vigilar las costosas colecciones de pintores famosos de criminales que busquen robarlas. Estas galerías vigilan las colecciones con video cámaras durante las noches, se busca que el número de video cámaras sea lo más pequeño posible pero que cada parte de la galería pueda ser visible por al menos una de ellas. Por lo tanto, la colocación de las cámaras debe ser estratégica. 

Definición[editar]

Definiendo el problema, se toma un plano del lugar para dar una mejor visión de donde se pueden colocar las cámaras. Así, se puede representar a la galería con un Polígono simple y a las posiciones de las cámaras con un punto en el polígono. Una cámara puede observar aquellos puntos en el polígono que pueden ser conectados con un segmento abierto que se encuentre dentro del polígono.

Para definir cuantas cámaras necesita el polígono, se debe expresar una cota del número de cámaras en termino del número de vértices del polígono ${\displaystyle n}$ y exponer el peor escenario que puede haber, que es tener un polígono simple con ${\displaystyle n}$ vértices, aunque existen casos donde dos polígonos que tienen un mismo número de vértices no pueden ser vigilados por el mismo número de cámaras.

Un polígono convexo puede ser vigilado con una sola cámara. Un polígono cóncavo necesita más de una.

Sea ${\displaystyle P}$ un polígono simple de ${\displaystyle n}$ vértices. Se procede a descomponer a ${\displaystyle P}$en triángulos, esto recibe el nombre de Triangulación de un polígono. Si se coloca una cámara por cada triángulo de la triangulación se necesitarán ${\displaystyle n-2}$ cámaras, debido a un teorema de la triangulación de un polígono que menciona que cualquier triangulación de un polígono simple con ${\displaystyle n}$ vértices contiene exactamente ${\displaystyle n-2}$ triángulos. ¹​ ²​

Esto se puede hacer mejor, buscando una estrategia para colocar las cámaras en algunas de las diagonales de los triángulos, ya que en esta posición una cámara podrá vigilar a 2 triángulos y se reduciría el número de cámaras a ${\displaystyle n/2}$ .¹​ Pero, aún se puede reducir mas el número de cámaras si se colocan en algunos de los vértices de ${\displaystyle P}$ por que un vértice puede ser incidente a varios triángulos y así mismo puede vigilarlos.

Colocación de las Cámaras[editar]

La estrategia para elegir los vértices donde se colocarán las cámaras es eligiendo un subconjunto de vértices de ${\displaystyle P}$, tal que cualquier triángulo en la triangulación contenga al menos un vértice seleccionado y colocar la cámara en ese sitio. Para elegir tal subconjunto, se le asigna una 3-coloración a ${\displaystyle P}$, que es asignar tres colores a los vértices de ${\displaystyle P}$ y se realiza de tal forma que cualquiera dos vértices conectados por una diagonal tienen asignado un color diferente, así cada triángulo tendrá asignado cada uno de los tres colores en sus vértices. Por último se eligen los vértices que contienen el mismo color y que sea el color que se encuentre en un número menor de vértices que los demás colores, y se colocan las cámaras. Esto reduce el número de cámaras a ${\displaystyle n/3}$ .¹​

3-coloración de un Polígono Simple[editar]

Se comienza realizando un Grafo dual a la triangulación realizada en ${\displaystyle P}$, este grafo dual tiene un nodo por cada triángulo en la triangulación. Hay un arco entre dos nodos ${\displaystyle a}$ y ${\displaystyle b}$ si el triángulo que corresponde a ${\displaystyle a}$ y el triángulo que corresponde a ${\displaystyle b}$ comparten una diagonal. Los arcos en este grafo dual son diagonales de la triangulación de ${\displaystyle P}$, ya que estas cortan a la triangulación en dos, esto quiere decir que este grafo dual es un árbol. ¹​ La 3-coloración se irá realizando con una Búsqueda en profundidad del árbol, manteniendo que todos los vértices de los triángulos que ya han sido visitados por la búsqueda ya han sido coloreados por cada uno de los tres colores y no existen 2 vértices conectados con el mismo color.

3-coloración de ${\displaystyle P}$, en una búsqueda de profundidad se va al nodo ${\displaystyle b}$ desde el nodo ${\displaystyle a}$, los vértices del triángulo de ${\displaystyle a}$ ya han sido coloreados, solo un vértice del triángulo de ${\displaystyle b}$ resta por ser coloreado, solo existe un color que queda para este vértice y es el color que no es usado por la diagonal compartida entre el triángulo de ${\displaystyle a}$ y el triángulo de ${\displaystyle b}$

Propiedades[editar]

A continuación se muestra una propiedad para la colocación de cámaras en un polígono simple:¹​ ²​

Teorema 1 Para un polígono simple con ${\displaystyle n}$ vértices, ${\displaystyle n/3}$ cámaras son ocasionalmente necesarias y siempre suficientes para tener cada punto en el polígono visible a al menos una de ellas.

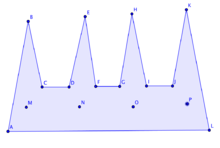
Esta teorema dice que la colocación de las cámaras no puede hacerse mejor y esto se debe a que existe una familia de polígonos simples que requieren de exactamente ${\displaystyle n/3}$ cámaras para poder ser vigilados, esta familia consiste de un polígono simple en forma de peine.

polígono simple en forma de peine con cámaras, ${\displaystyle n=12}$ cada diente del peine necesita ser vigilado por una cámara y justo se tienen ${\displaystyle n/3}$ dientes

.

Son ocasionalmente necesarias por que aunque existan polígonos simples que les basten menos de ${\displaystyle n/3}$ cámaras, como el Polígono convexo, siempre va existir esta familia que no pueda reducir el número de cámaras ${\displaystyle$, pero por otro lado siempre son suficientes por que para todas las familias de polígonos simples siempre va a bastar tener ${\displaystyle n/3}$ cámaras.

El Problema de las colegialas de Kirkman es un problema de matemática, relacionado con la rama de la combinatoria, propuesto por el matemático británico Thomas Kirkman en 1850, como la consulta VI en el Diario de la dama y el caballero.

Su enunciado es el siguiente:

Quince alumnas salen formadas de tres en fondo durante siete días seguidos: se requiere formarlas cada día de manera que al terminar la semana no haya habido dos de ellas que hayan caminado juntas (o sea, en la misma fila) más de una vez.¹​²​

Solución[editar]

Si se numeran a las alumnas del 01 al 15, el siguiente arreglo es una solución:

Domingo	Lunes	Martes	Miércoles	Jueves	Viernes	Sábado
01, 06, 11	01, 02, 05	02, 03, 06	05, 06, 09	03, 05, 11	05, 07, 13	11, 13, 04
02, 07, 12	03, 04, 07	04, 05, 08	07, 08, 11	04, 06, 12	06, 08, 14	12, 14, 05
03, 08, 13	08, 09, 12	09, 10, 13	12, 13, 01	07, 09, 15	09, 11, 02	15, 02, 08
04, 09, 14	10, 11, 14	11, 12, 15	14, 15, 03	08, 10, 01	10, 12, 03	01, 03, 09
05, 10, 15	13, 15, 06	14, 01, 07	02, 04, 10	13, 14, 02	15, 01, 04	06, 07, 10

Una solución a este problema es un ejemplo de un sistema triple de Steiner S (2,3,n)

En el "problema de las doce monedas" se propone identificar la moneda falsa, entre un grupo de doce monedas, empleando 3 pesadas de balanza.

La moneda falsa tiene un peso distinto de las otras, y hay que averiguar si esta moneda pesa más o menos que las otras.

En su versión de 12 monedas habría aparecido en 1945, sin que se sepa su procedencia.

El problema admite una generalización inmediata aumentando el número de monedas y de pesadas: ¿Cuál es el máximo de monedas para "n" pesadas?

Ofrecemos aquí tres soluciones del problema.

1ª Solución[editar]

La primera solución, de fácil generalización para más pesadas, se explica a continuación:

La 1ª pesada la realizamos así:

• Brazo derecho: 1,2,3,4
• Brazo izquierdo: 5,6,7,8
• Mesa: 9,10,11,12

En la 2ª pesada, rotamos los grupos de tres monedas:

• Brazo derecho: 1,10,11,12
• Brazo izquierdo: 5,2,3,4
• Mesa: 9,6,7,8

• Si la inclinación de la balanza no cambia, la moneda falsa está entre las tres que no hemos rotado: 1, 5, 9.
• Si la inclinación de la balanza cambia, podemos identificar qué grupo de los que hemos rotado tiene la moneda falsa.

Y nos queda la 3ª pesada para identificar entre 3 monedas cuál es la falsa: sólo tenemos que pesar dos de ellas, pues como ya tenemos información de anteriores pesadas podemos así identificarla.

Generalización[editar]

Veamos primero el método A: procedimiento cuando conocemos que la moneda pesa más (si pesa menos será análogo).

Veamos un ejemplo con 9 monedas: Formamos tres grupos de tres monedas cada uno y se pesa el grupo 1 frente al grupo 2.

• Si existe equilibrio la moneda falsa está en el grupo 3.
• Si no existe equilibrio la inclinación de la balanza indica cuál de los grupos es el que tiene la moneda falsa (pues conocemos si pesa más o menos).

De la pesada anterior quedan tres monedas que contiene la falsa. Se pesa la moneda A contra la moneda B, e identificamos fácilmente cual es la falsa.

La clave de la generalización reside en el método A, y consiste en identificar el grupo de ${\displaystyle 3^{n}}$ monedas con n pesadas: Formamos 3 grupos, pesamos 2 de ellos e identificamos el grupo problemático. Y repetimos el proceso hasta obtener una moneda.

Veamos ahora el caso general:

El problema admite una generalización a 4 pesadas añadiendo una nueva fila de 9 monedes en cada uno de los 3 grupos: 13 monedas en cada grupo... Rotaremos los grupos de 9 monedas y razonamos igual que antes: si la posición cambia identificamos el grupo de 9 con la moneda falsa y le aplicamos el método A. Si la posición no cambia, quitamos los grupos de 9 y nuestras condiciones son ahora las del problema de 12 monedas con 3 pesadas.

Con 5 pesadas añadiremos otra fila más de 27 monedas en cada uno de los 3 grupos: 40 monedas en cada grupo. Y procedemos análogamente como en el caso anterior.

Como estamos agregando potencias de 3 en cada paso, obtendremos la suma de una progresión geométrica:

Monedas	Pesadas	Justificación
3	2
12	3	${\displaystyle 3+3^{2}=12}$
39	4	${\displaystyle 12+3^{3}=39}$
120	5	${\displaystyle 39+3^{4}=120}$
363	6	${\displaystyle 120+3^{5}=363}$
120	7	${\displaystyle 363+3^{6}=1092}$
${\displaystyle {\frac {3^{n}-3}{2}}}$	n

¿Cuál es el máximo de monedas para "n" pesadas?[editar]

Un problema más difícil es éste, y precisaremos de la 2ª solución. No obstante, ofrecemos un argumento intuitivo:

Para (n+1) pesadas analicemos el máximo de monedas, entre balanza y mesa:

Un máximo en la balanza es ${\displaystyle 3^{n}}$ monedas, pues después de la 1ª inclinación de balanza nos quedan n pesadas y ${\displaystyle 3^{n}}$ es el máximo de monedas. Pero como tiene que ser par (dos platillos), en la balanza habrá hasta ${\displaystyle 3^{n}-1}$como máximo.

Veamos el máximo de monedas en la mesa:

si la moneda falsa está en la mesa entonces hay equilibrio en la 1ª pesada y dispondremos de monedas "buenas": Escogemos ${\displaystyle 3^{n-1}}$ monedas de la mesa y las pesamos con otras tantas "buenas", si está ahí la moneda falsa el método A asegura encontrarla con (n-1) pesadas que nos quedan; si hay equilibrio repetimos el proceso con ${\displaystyle 3^{n-2}}$ monedas, con (n-2) pesadas que nos quedan;...; si hay equilibrio repetimos el proceso con ${\displaystyle 3^{2}}$monedas con otras 9 "buenas"; si hay equilibrio repetimos el proceso con ${\displaystyle 3^{1}}$ monedas con otras 3 "buenas"; finalmente, si hay equilibrio pesamos la última moneda con 1 "buena" para saber si pesa más o menos, con la última pesada que nos queda. Sumando todas las monedas de la mesa que hemos pesado, tenemos una progresión geométrica:

${\displaystyle S(n)=1+3+9+...+3^{n-1}={\frac {3^{n}-1}{2}}}$

que, curiosamente, coincide con la mitad del máximo de la balanza, es decir como cada brazo de balanza.

Finalmente, sumamos el máximo obtenido en la mesa y en la balanza, y obtenemos otra suma de progresión geométrica:

${\displaystyle 1+3+9+...+3^{n-1}+3^{n}-1=3+9+...+3^{n-1}+3^{n}}$

que coincide con la obtenida en la generalización.

2ª Solución[editar]

Primero veamos un método de separación en grupos, parecido al método A descrito antes, que consigue aislar la moneda falsa en grupos de 3, 9, 27,.., 3^n para monedas "orientadas" (procedentes de la 1ª inclinación de balanza):

Para 3 monedas "orientadas", la solución es pesar 2 de ellas.

Si tenemos 9 monedas "orientadas", pondremos en cada brazo dos "monedas pesadas" (procedentes del brazo inclinado en la 1ª pesada) que denotamos (2+), y una "moneda ligera" (procedente del brazo opuesto) que denotamos (1-):

brazo izquierdo	brazo derecho	mesa
(2+)	(1-) (2+)	(1-) monedas restantes

Según se incline la balanza identificamos un grupo de 3 donde está la moneda falsa.

Análogamente, si tenemos 27 monedas "orientadas" identificamos un grupo de 9 monedas:

brazo izquierdo	brazo derecho	mesa
(6+)	(3-) (6+)	(3-) monedas restantes

Y en general, formamos 3 grupos de ${\displaystyle 3^{n+1}}$ monedas:

brazo izquierdo	brazo derecho	mesa
(${\displaystyle 2*3^{n}}$ +)	(${\displaystyle 3^{n}}$ -) (${\displaystyle 2*3^{n}}$ +)	(${\displaystyle 3^{n}}$ -) monedas restantes

En general, para 3^n monedas "orientadas" necesitamos n pesadas: si 3 es el máximo para 1 pesada, no podemos exceder 3 grupos de 3 monedas en 2 pesadas; ni 3 grupos de 9 monedas en 3 pesadas...etc; por tanto:

El máximo de monedas "orientadas" con n pesadas es ${\displaystyle 3^{n}}$ .

Veamos ahora el procedimiento general:

Ahora sólo queda ver cómo configurar la primera pesada.

Sea la sucesión ${\displaystyle X(n)}$ el máximo de monedas para ${\displaystyle n}$ pesadas.

Calculemos ${\displaystyle X(n+1)}$ : máximo de monedas para (n+1) pesadas:

Podremos poner en los dos brazos hasta ${\displaystyle 3^{n}}$ monedas, que es el máximo de monedas "orientadas" con n pesadas. Y como la balanza exige un número par, restamos 1:

${\displaystyle Balanza=3^{n}-1}$

Y en la mesa pondremos X(n)+1: sumamos 1 por no tener la exigencia de pesar un número par, pues ahora tenemos monedas extra procedentes del equilibrio de la balanza:

${\displaystyle Mesa=X(n)+1}$

Calculamos el total entre los brazos y la mesa:

${\displaystyle Total=Balanza+Mesa}$

${\displaystyle X(n+1)=3^{n}-1+X(n)+1=3^{n}+X(n)}$

Por tanto, X(n) tiene estructura de suma de una progresión geométrica de razón r= 3.

El primer término de la sucesión X(n) es:

${\displaystyle X(2)=balanza+mesa=2+1=3}$

pues en la mesa es evidente que sólo podemos poner 1 moneda, y en la balanza ya hemos argumentado que ha de ser igual a ${\displaystyle 3^{1}-1=2}$.

• ${\displaystyle X(3)=3^{2}+X(2)=12}$
• ${\displaystyle X(4)=3^{3}+X(3)=39}$
• ${\displaystyle X(5)=3^{4}+X(4)=120}$

Así pues, ${\displaystyle X(n+1)=3+9+27+...+3^{n}=3*(3^{n}-1)/2}$

${\displaystyle X(n)=(3^{n}-3)/2}$. Como queríamos demostrar

Además, por ser X(n) suma de progresión geométrica se cumple que cada brazo y la mesa tienen las mismas monedas, pues:

${\displaystyle mesa=balanza/2}$

${\displaystyle X(n)+1={\frac {3^{n}-1}{2}}}$

Veamos un esquema de los primeros términos, así como la configuración de la primera pesada para cada caso.

Primera pesada
número de pesadas	brazo izquierdo	brazo derecho	mesa
2	1	1	1
3	4	4	${\displaystyle 4=X(2)+1}$
4	13	13	${\displaystyle 13=X(3)+1}$
5	40	40	${\displaystyle 40=X(4)+1}$
6	121	121	${\displaystyle 121=X(5)+1}$
7	364	364	${\displaystyle 364=X(6)+1}$

Veamos el ejemplo de 12 monedas:

brazo izquierdo	brazo derecho	mesa
1,2,3,4	5,6,7,8	9,10,11,12

a) Si se equilibra, atacamos las 4 bolas restantes formando un grupo de 3 monedas, pues ahora sí podemos pesar un número impar en los dos brazos, al tener monedas buenas:

brazo izquierdo	brazo derecho	mesa
9,10	11,12

b) Y si se inclina, tenemos ${\displaystyle 8=3^{2}-1}$ monedas "orientadas" y aplicamos el método de separación descrito:

brazo izquierdo	brazo derecho	mesa
1 2 5 3 4 6 7	8

• Si se equilibra, está en el grupo (7,8), evidentemente.
• Si se inclina como la 1ª pesada, está en el grupo (1,2,6).
• Si no, estará en el grupo (3,4,5).

3er Solución[editar]

Esta tercer solución es una forma más "matemática" y menos "lógica" de resolver el problema.

Se van a hacer 3 pesadas, de dos grupos de 4 monedas, dejando 4 afuera. Las tres pesadas se hacen independientemente del resultado de la anterior.

Los grupos de monedas a pesar se eligen de forma que:

• Ninguna moneda quede las 3 veces sin pesarse (en el grupo "Afuera") pues de ser así, podríamos identificarla pero no podríamos asegurar si es más pesada o más liviana.
• Ningún par de monedas quede las tres veces en el mismo plato, o las tres veces en platos opuestos. Si así sucediera, no podríamos definir cuál de las dos es la diferente.

Una de las formas de armar los grupos para las tres pesadas cumpliendo los criterios anteriores es la siguiente:

Núm. Pesada	Izquierda	Derecha	Afuera
Primera	1 2 3 4	5 6 7 8	9 10 11 12
Segunda	1 2 7 12	3 4 9 10	5 6 8 11
Tercera	2 3 8 9	4 5 10 11	1 6 7 12

Dados los grupos anteriores, armamos la siguiente matriz donde le asignamos a cada moneda la letra I, D o A según quede en el plato Izquierdo, en el plato Derecho, o Afuera. Esta matriz se utiliza para identificar las distintas opciones de resultados posibles.

Tabla de pesadas:

Moneda	1	2	3	4	5	6	7	8	9	10	11	12
Pesada 1	I	I	I	I	D	D	D	D	A	A	A	A
Pesada 2	I	I	D	D	A	A	I	A	D	D	A	I
Pesada 3	A	I	I	D	D	A	A	I	I	D	D	A

Cada pesada puede arrojar 3 resultados posibles que identificamos con las letras "I", "D" y el signo "=" según se incline hacia la Izquierda, hacia la Derecha, o quede balanceada.

Esto nos arroja 27 resultados posibles. (3 ^ 3) que representaremos con los 3 símbolos. Ej: Si la primera pesada se inclina a la Derecha, la segunda a la Izquierda, y la última queda balanceada, lo representamos como D I =

1er	'2da'	'3er'	'Resultado'
I	I	I
I	I	D
I	I	=
I	D	I

.... y así las 27 combinaciones...

Ahora evaluamos las 24 situaciones diferentes que pueden darse. A saber: Moneda 1 más pesada; Moneda 1 más liviana, Moneda 2 más pesada, Moneda 2 más liviana; y las representamos, respectivamente como: 1+, 1-, 2+. 2-...

Para cada situación, miramos el resultado que daría en la matriz de pesadas y lo buscamos en la matriz de resultados.

Ej: Moneda 1 más pesada (miramos la primera columan de la matriz de pesadas) y vemos que el resultado seríaI I = Pues la moneda 1 estaba en el plato izquierdo en la primera y segunda pesada, y quedó afuera en la última, por lo que ubicamos ese resultado en la grilla corerspondiente:

1er	'2da'	'3er'	'Resultado'
I	I	I
I	I	D
I	I	=	1+
I	D	I

Segunda situación posible: Moneda 1 más liviana. En este caso, el resultado de las pesadas es D D = y ubicamos el 1- donde corresponde en la grilla de resultados.

Luego de analizar todas las "situaciones" posibles vamos a tener 3 resultados que nunca se dan, y el resto de los resultados que corresponden a cada una de las 24 situaciones posibles.

Si alguna de las "situaciones" repite el resultado es que hemos elegido mal los grupos de monedas a pesar.

Para el ejemplo de grupos dado, la tabla completa de resultados es la siguiente:

Tabla de resultados:

1er	2da	3er	Resultado
I	I	I	2+
I	I	D	Nunca se da
I	I	=	1+
I	D	I	3+
I	D	D	4+
I	D	=	7-
I	=	I	5-
I	=	D	8-
I	=	=	6-
D	I	I	4-
D	I	D	3-
D	I	=	7+
D	D	I	Nunca se da
D	D	D	2-
D	D	=	1-
D	=	I	8+
D	=	D	5+
D	=	=	6+
=	I	I	10-
=	I	D	9-
=	I	=	12+
=	D	I	9+
=	D	D	10+
=	D	=	12-
=	=	I	11-
=	=	D	11+
=	=	=	Nunca se da

Entonces... La forma de resolver hallar la moneda sería la siguiente:

1. Realizar las tres pesadas con los grupos de monedas que definimos.
2. Registrar los resultados de las tres pesadas.
3. Buscar el resultado en la tabla de resultados.

Ej. Si la primera pesada se inclinó hacia la izquierda; la segunda a la derecha, y la tercera quedó balanceada, (I D =) la moneda diferente es la nro 7, y es más liviana que el resto (7 -)