PROBLEMAS MATEMÁTICOS

El problema del caballo es un antiguo problema matemático en el que se pide que, teniendo una cuadrícula de n x n casillas y un caballo de ajedrez colocado en una posición cualquiera ( x, y ), el caballo pase por todas las casillas y una sola vez. Lo que resulta en n²-1 movimientos.

Solución para 63 saltos de caballo por las 64 casillas.

Muchos matemáticos han buscado una solución matemática a este problema, entre ellos Leonhard Euler.

Se han encontrado muchas soluciones a este problema y de hecho no se sabe con seguridad de cuántas maneras diferentes es posible solucionarlo.

Algunas variaciones de este problema han sido estudiadas por los matemáticos, tales como:

• Buscar soluciones cíclicas, en la cual se debe llegar a la misma casilla de la cual se partió.
• Tableros de diferente número de columnas o diferente número de filas.
• Juegos de dos jugadores basados en la idea.
• Problemas usando ligeras variaciones en la forma de moverse el caballo.

El problema del caballo es una forma del problema más general problema de la ruta Hamiltoniana en la teoría de grafos.

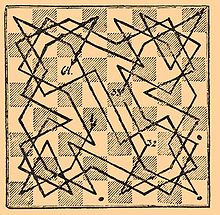
A la derecha podemos apreciar una de las posibles soluciones en un tablero de ajedrez convencional de ocho columnas por ocho filas. Abajo, una solución cíclica en que la casilla de destino es justo la anterior a la de partida.

63	14	37	24	51	26	35	10
22	39	62	13	36	11	50	27
15	64	23	38	25	52	9	34
40	21	16	61	12	33	28	49
17	60	1	44	29	48	53	8
2	41	20	57	6	55	32	47
59	18	43	4	45	30	7	54
42	3	58	19	56	5	46	31

El problema del caballo en la literatura[editar]

Solución del problema del caballo para la novela La vida instrucciones de uso.

Los capítulos de la novela La vida instrucciones de uso (1978) de Georges Perec siguen una ordenación que corresponde a una solución del problema del caballo sobre una cuadrícula de 10×10. La solución fue encontrada experimentalmente por el mismo autor.

El problema de la división de los 17 caballos o del reparto de los 17 caballos es un problema planteado por el matemático italiano Tartaglia en el siglo XVI.

Un hombre muere y deja a sus tres hijos 17 caballos que deben ser divididos en proporción ${\displaystyle {\frac {1}{2}};{\frac {1}{3}};{\frac {1}{9}}}$. ¿Pueden cumplir los hermanos con el deseo de su padre?

El problema[editar]

Calculando el número de caballos que corresponde a cada hijo:

${\displaystyle 17\cdot {\cfrac {1}{2}}=8,5\;,\quad 17\cdot {\cfrac {1}{3}}=5,{\overset {\frown }{6}}\;,\quad 17\cdot {\cfrac {1}{9}}=1,{\overset {\frown }{8}}}$

La parte fraccionaria no es válida como solución, dado que cada uno de los herederos quiere un número de caballos enteros.

Para soluciones el problema hay que percatarse de dos detalles. Primero: el número de caballos ha de ser un múltiplo entero de las partes en que se divide la herencia si se quiere obtener divisiones enteras. Segundo detalle: la suma de las partes en la que se hace la división ha de sumar el total.

La suma de las partes:

${\displaystyle {\cfrac {1}{2}}+{\cfrac {1}{3}}+{\cfrac {1}{9}}\quad =\quad {\cfrac {9}{18}}+{\cfrac {6}{18}}+{\cfrac {2}{18}}\quad =\quad {\cfrac {17}{18}}}$

La suma de las partes es de diecisiete dieciochoavos y no dieciocho dieciochoavos como tendría que ser. Por lo tanto lo que hacen es pedir un caballo prestado y repartir la herencia.

${\displaystyle 18\cdot {\cfrac {1}{2}}=9\;,\quad 18\cdot {\cfrac {1}{3}}=6\;,\quad 18\cdot {\cfrac {1}{9}}=2}$

que da por resultado números enteros, se puede ver que:

${\displaystyle 9+6+2=17}$

Con lo que les sobra un caballo y pueden devolverselo a quien se lo prestó.

El problema de los treinta y seis oficiales es un rompecabezas matemático propuesto por Leonhard Euler en 1782 ¹​

El problema pregunta si es posible colocar a treinta y seis oficiales de seis regimientos diferentes y de cada uno de los seis grados (en cada regimiento) en un cuadrado de 6x6 de forma que no coincidan dos oficiales del mismo rango o del mismo regimento en ninguna fila y en ninguna columna. Esta disposición forma un cuadrado greco-latino.

Euler demostró que el problema podía resolverse siempre que el lado del cuadrado fuese impar o multiplo de cuatro (par de clase par) y conjeturó que no existía ninguna solución posible cuando era impar de clase par (multiplo de 2 que no es multiplo de 4).

Gaston Tarry en 1901²​³​ demostró la conjetura de Euler para el orden 6.

En 1960, Parker, Bose, y Shrikhande⁴​ demostraron que la conjetura de Euler es falsa para todo n ≥ 10. Por lo tanto, existen cuadrados greco-latinos de lado n para todos los n ≥ 3, excepto n = 6.

Además del caso del 6x6 el único otro caso en que el problema no tiene solución equivalente es el caso de 2x2, es decir, cuando hay 4 oficiales.