En estática, el problema de apilado de bloques (a veces conocido como La torre inclinada de Lira, también problema del apilado (o apilamiento) de libros u otras formas similares) es un desafío mental relacionado con el apilamiento de bloques en el borde de una mesa.
Declaración[editar]
El problema se expresa:
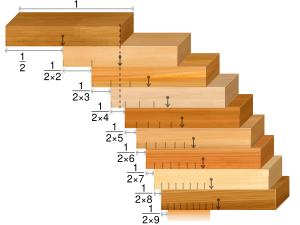
Disponga N bloques rectangulares rígidos idénticos en un una pila estable en el borde de una mesa de tal forma que maximice la distancia que sobresale.
Historia[editar]
Paterson et al. provee una larga lista de referencias a este problema que incluyen hasta libros de texto mecánica del siglo XIX.
Variantes[editar]
Ancho fijo[editar]
En este caso todos los bloques de la pila tienen el mismo ancho para todo nivel. En el caso ideal de bloques perfectamente rectangulares la solución para bloques de idéntico ancho la solución está dada por veces el ancho de un bloque. Esta es una serie armónica divergente, un medio de la serie suma parcial. Dado que la serie es divergente, el maximal de la medida que puede sobresalir tiende a infinito a medida que aumenta, lo que implica que es posible sobresalir una distancia arbitraria, con la cantidad de bloques suficientes.
| N | sobresalido | |||
|---|---|---|---|---|
| Expresado como fracción | Decimal | Medida relativa | ||
| 1 | 1 | /2 | 0.5 | |
| 2 | 3 | /4 | 0.75 | |
| 3 | 11 | /12 | ~0.91667 | |
| 4 | 25 | /24 | ~1.04167 | |
| 5 | 137 | /120 | ~1.14167 | |
| 6 | 49 | /40 | 1.225 | |
| 7 | 363 | /280 | ~1.29643 | |
| 8 | 761 | /560 | ~1.35893 | |
| 9 | 7 129 | /5 040 | ~1.41448 | |
| 10 | 7 381 | /5 040 | ~1.46448 | |
| N | Sobresalido máximo | |||
|---|---|---|---|---|
| Expresado como fracción | Decimal | Medida relativa | ||
| 11 | 83 711 | /55 440 | ~1.50994 | |
| 12 | 86 021 | /55 440 | ~1.55161 | |
| 13 | 1 145 993 | /720 720 | ~1.59007 | |
| 14 | 1 171 733 | /720 720 | ~1.62578 | |
| 15 | 1 195 757 | /720 720 | ~1.65911 | |
| 16 | 2 436 559 | /1 441 440 | ~1.69036 | |
| 17 | 42 142 223 | /24 504 480 | ~1.71978 | |
| 18 | 14 274 301 | /8 168 160 | ~1.74755 | |
| 19 | 275 295 799 | /155 195 040 | ~1.77387 | |
| 20 | 55 835 135 | /31 039 008 | ~1.79887 | |
| N | Sobresalido máximo | |||
|---|---|---|---|---|
| Expresado como fracción | Decimal | Medida relativa | ||
| 21 | 18 858 053 | /10 346 336 | ~1.82268 | |
| 22 | 19 093 197 | /10 346 336 | ~1.84541 | |
| 23 | 444 316 699 | /237 965 728 | ~1.86715 | |
| 24 | 1 347 822 955 | /713 897 184 | ~1.88798 | |
| 25 | 34 052 522 467 | /17 847 429 600 | ~1.90798 | |
| 26 | 34 395 742 267 | /17 847 429 600 | ~1.92721 | |
| 27 | 312 536 252 003 | /160 626 866 400 | ~1.94573 | |
| 28 | 315 404 588 903 | /160 626 866 400 | ~1.96359 | |
| 29 | 9 227 046 511 387 | /4 658 179 125 600 | ~1.98083 | |
| 30 | 9 304 682 830 147 | /4 658 179 125 600 | ~1.99749 | |
Ancho variable[editar]
El apilado con ancho variable contrarrestando con contrapeso puede permitir sobresalir más que lo que permite una pila de ancho fijo. Incluso con sólo tres bloques utilizando dos bloques cuyos pesos se contrarrestan permite que se sobresalga 1 (una unidad, el ancho de un bloque) mientras que para el caso sencillo de ancho fijo es idealmente como máximo 11/12. Tan Paterson et al. (2007) mostró que de forma asintótica que el valor máximo que puede sobresalir para el caso de ancho variable es proporcional al a la raíz cúbica del número de bloques, en contraste con el caso de ancho fijo en el cual es proporcional al logaritmo del número de bloques.
Robustez[editar]
Hall (2005) trata este problema, muestra que es robusto a nonidealizations como esquinas de bloque redondeado y precisión finita de colocación de bloque, e introduce varias variantes que incluyen nonzero fuerzas de fricción entre bloques adyacentes.
Referencias[editar]
- «Fun with stacking blocks». American Journal of Physics 73 (12): 1107-1116. 2005. Bibcode:2005AmJPh..73.1107H. doi:10.1119/1.2074007Plantilla:Inconsistent citations.
- Paterson, Mike; Peres, Yuval; Thorup, Mikkel; Winkler, Peter; Zwick, Uri(2007). «Maximum overhang».
.
Enlaces externos[editar]
- Weisstein, Eric W. "Libro Stacking Problema". MathWorld.
- «Building an Infinite Bridge». PBS Infinite Series. 4 de mayo de 2017. Consultado el 3 de septiembre de 2018.
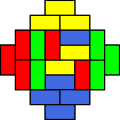
diamante azteca de orden n está formado por todos los cuadrados de una cuadrícula cuyos centros (x, y) satisfacen la condición de que |x| + |y| ≤ n, siendo n un número entero dado. La rejilla consiste en una serie de cuadrados de lado unidad con el origen como un vértice de 4 de ellos, de modo que tanto x como yson números semienteros.1
El teorema del diamante azteca indica que el número de maneras distintas posibles de recubrir con un teselado en dominó un diamante azteca de orden n es:2
- 2n(n+1)/2
El teorema del círculo ártico afirma que un recubrimiento aleatorio de un gran diamante azteca tiende a ordenarse fuera de un cierto círculo.3
Es común colorear las fichas de la manera siguiente:
- Primero, considérese un coloreado del diamante como el de un tablero de ajedrez.
- Cada dominó cubrirá exactamente un cuadrado negro y otro blanco.
- Las teselas verticales donde el cuadrado superior cubre un cuadrado negro, se colorean de negro, y las otras teselas verticales, en un segundo color.
- Se aplica el mismo procedimiento a las teselas horizontales, con izquierda y derecha
En matemática, el problema del final feliz (nombrado así por Paul Erdős, porque condujo a la relación y posterior matrimonio entre George Szekeres y Esther Klein, un «final feliz» de cuento) es el siguiente enunciado:
Cualquier conjunto de 5 puntos en el plano en posición general (no colineales) tiene un subconjunto de 4 puntos que son los vértices de un cuadrilátero convexo.
Éste es uno de los resultados que dio inicio al desarrollo de la teoría de Ramsey.
El Problema de final feliz puede ser probado por un simple análisis de casos:
- Caso 1: Si los cinco puntos forman los vértices de un pentágono convexo, pueden ser elegidos 4 puntos cualquiera.
- Caso 2: Si una configuración de puntos forma un triángulo con dos puntos interiores; los dos puntos interiores y dos vértices del triángulo pueden ser elegidos.
- Caso 3: Si una configuración de puntos forma un cuadrílatero con un punto interior,este cuadrílatero es convexo.
La conjetura de Erdős-Szekeres es la extensión entre el número de puntos en un conjunto de puntos de posición general y su polígono convexo más grande construible. Aun no se tiene una solución general, pero se manejan casos particulares y cotas superiores e inferiores.






No hay comentarios:
Publicar un comentario