PROBLEMAS MATEMÁTICOS

problema de Dirichlet es un problema que consiste en hallar una función que es la solución de una ecuación en derivadas parciales (EDP) en el interior de un dominio de ${\displaystyle \mathbb {R} ^{n}}$ (o más generalmente una variedad diferenciable) que tome valores prescritos sobre el contorno de dicho dominio.

El problema de Dirichlet puede resolverse para muchas EDPs, aunque originalmente fue planteada para la ecuación de Laplace. En este caso el problema puede enunciarse como sigue:

Dada una función ${\displaystyle f}$ con valores en todos los puntos del contorno de una región en ${\displaystyle \mathbb {R} ^{n}}$. ¿Existe una única función continua ${\displaystyle u}$ dos veces continuamente diferenciable en el interior y continua en el contorno, tal que u es armónica en el interior y ${\displaystyle u=f}$ en el contorno?

Este requisito se denomina condición de contorno de Dirichlet. En este problema es fundamental probar la existencia de la solución; la unicidad viene dada utilizando el principio del máximo.

El problema de Dirichlet debe su nombre a Lejeune Dirichlet, quien propuso una solución para un método variacional el cual se conoce como principio de Dirichlet. La existencia de una solución única es muy plausible por el 'argumento físico': cualquier distribución de carga sobre el contorno, para las leyes de la electrostática, deberá determinar un potencial eléctrico como solución.

Sin embargo, Weierstrass encontró una falla al argumento de Dirichlet, y una demostración rigurosa de la existencia fue encontrada recién en 1900 por Hilbert. Resultó entonces que la existencia de una solución depende delicadamente de la suavidad del contorno y de los datos prescritos.

Solución general[editar]

Para un dominio ${\displaystyle D}$ teniendo la suavidad suficiente sobre el contorno ${\displaystyle \partial D}$, la solución general al problema de Dirichlet es:

${\displaystyle u(x)=\int _{\partial D}\nu (s){\frac {\partial G(x,s)}{\partial n}}ds}$

donde

${\displaystyle G(x,y)}$ es la función de Green para la ecuación en derivadas parciales, y

${\displaystyle {\frac {\partial G(x,s)}{\partial n}}={\widehat {n}}\cdot \nabla _{s}G(x,s)=\sum _{i}n_{i}{\frac {\partial G(x,s)}{\partial s_{i}}}}$

es la derivada de la función de Green a lo largo del vector unitario normal apuntando hacia el interior ${\displaystyle {\widehat {n}}}$. La integración se realiza sobre el contorno, con la medida ${\displaystyle ds}$. La función ${\displaystyle \nu (s)}$ está dada por la solución única de la ecuación integral de Fredholm de segunda clase,

${\displaystyle f(x)=-{\frac {\nu (x)}{2}}+\int _{\partial D}\nu (s){\frac {\partial G(x,s)}{\partial n}}ds.}$

La función de Green a utilizar en la integral de arriba desaparece en el contorno:

${\displaystyle G(x,s)=0\,}$

para ${\displaystyle s\in \partial D}$ y ${\displaystyle x\in D}$. Tal función de Green usualmente es una suma de las funciones de Green del campo libre una solución armónica a la ecuación diferencial.

Existencia[editar]

El problema de Dirichlet para funciones armónicas siempre tiene solución, y esa solución es única cuando el contorno es suficientemente suave y ${\displaystyle f(s)}$ es continua. Más precisamente, tiene solución cuando:

${\displaystyle \partial D\in C^{(1,\alpha )}}$

para ${\displaystyle 0<\alpha \,}$, donde ${\displaystyle C^{(1,\alpha )}\,}$ es la condición de Hölder.

Las condiciones anteriores pueden relajarse pudiéndose probar que el problema de Dirichlet admite solución continua para un dominio convexo (sin requerir condiciones de suavidad) o cuando cada punto del contorno pertenece a una bola cerrada íntegramente contenida en el conjunto complementario del interior del dominio (condición de la bola cerrada exterior).

Unicidad[editar]

Supongase la existencia de dos funciones armónicas en una región R simplemente conexa que cumplen:

${\displaystyle \Delta u_{1}=\Delta u_{2}\qquad \forall x\in R\qquad y\qquad u_{1}|_{\delta R}=u_{2}|_{\delta R}=f(x)\qquad \forall x\in \delta R}$

Se construye la siguiente función:

${\displaystyle u_{0}=u_{1}-u_{2}\qquad \forall x\in R}$

Por construcción la función dada cumple:

${\displaystyle \Delta u_{0}=\Delta (u_{1}-u_{2})=\Delta u_{1}-\Delta u_{2}=0\qquad y\qquad u_{0}|_{\delta R}=u_{1}|_{\delta R}-u_{2}|_{\delta V}=0}$

Integrando la norma del gradiente de ${\displaystyle u_{0}}$ en todo el volumen delimitado por el contorno y aplicando el teorema de Green se tiene que:

${\displaystyle \int _{R}\nabla u_{0}\cdot \nabla u_{0}dV=\int _{R}\nabla \cdot (u_{0}\nabla u_{0})dV-\int _{R}u_{0}\Delta u_{0}dV=\int _{\delta R}u_{0}\nabla u_{0}\cdot dS-\int _{R}u_{0}\Delta u_{0}dV}$

pero

${\displaystyle \Delta u_{0}=0\qquad \Rightarrow \qquad \int _{R}u_{0}\Delta u_{0}dV=0}$

${\displaystyle u_{0}|_{\delta R}=0\qquad \Rightarrow \qquad \int _{\delta R}u_{0}\nabla u_{0}\cdot dS=0}$

de modo que:

${\displaystyle \int _{R}\nabla u_{0}\cdot \nabla u_{0}dV=\int _{R}||\nabla u_{0}||^{2}dV=0\qquad \Rightarrow \qquad \nabla u_{0}=0\qquad \forall x\in R\qquad \Rightarrow \qquad u_{0}=cte\qquad \forall x\in R}$

Dado que ${\displaystyle u_{0}|_{\delta R}=0}$ se tiene finalmente que:

${\displaystyle u_{0}=0\qquad \forall x\in R\qquad \Rightarrow \qquad u_{1}=u_{2}\qquad \forall x\in R}$

Construcción de Perron[editar]

Artículo principal: Método de Perron

Cuando el problema de Dirichlet se plantea sobre un conjuto abierto ${\displaystyle \scriptstyle \Omega }$ y acotado de ${\displaystyle \scriptstyle \mathbb {R} ^{n}}$ y ${\displaystyle \scriptstyle f}$ denota una función real continua sobre la frontera ${\displaystyle \scriptstyle \partial \Omega }$ puede definirse la llamada construcción de Perron que convierte el problema de Dirichlet en un problema de minimización. Si se define el conjunto de Perron ${\displaystyle \scriptstyle S_{f}}$ para ${\displaystyle \scriptstyle f}$ como el conjunto de funciones reales continuas ${\displaystyle \scriptstyle u}$ definidas sobre ${\displaystyle \scriptstyle {\bar {\Omega }}}$ que son subarmónicas sobre ${\displaystyle \scriptstyle \Omega }$ y que satisfacen que ${\displaystyle \scriptstyle u\leq f}$ sobre ${\displaystyle \scriptstyle \partial \Omega }$. Nótese que este conjunto es no vacío ya que contiene la función constante para ${\displaystyle \scriptstyle u(x)=m}$, siendo para ${\displaystyle \scriptstyle m}$ el mínimo de la función ${\displaystyle \scriptstyle f}$ sobre la frontera. Puede probarse que la siguiente función:

${\displaystyle {\bar {f}}=\sup\{u(x)|u\in S_{f}\}}$

es solución del problema de Dirichlet buscado cuando la frontera es tal que el problema admite solución única. Aún cuando la función anterior no sea una solución del problema de Dirichlet por irregularidades en la frontera, puede probarse que sigue siendo una función armónica sobre para ${\displaystyle \scriptstyle \Omega }$.

Ejemplo: el disco unitario en dos dimensiones[editar]

En algunos casos simples el problema de Dirichlet puede resolverse en forma explícita. Por ejemplo, la solución para el problema de Dirichlet para un disco unitario en ${\displaystyle \mathbb {R} ^{2}}$ está dado por la fórmula integral de Poisson.

Si ${\displaystyle f}$ es una función continua sobre el contorno ${\displaystyle \partial D}$ del disco unitario abierto ${\displaystyle D}$, entonces la solución al problema de Dirichlet es ${\displaystyle u(z)}$ dado por:

${\displaystyle u(z)={\begin{cases}{\cfrac {1}{2\pi }}\int _{0}^{2\pi }f(e^{i\psi }){\cfrac {1-\vert z\vert ^{2}}{\vert z-e^{i\psi }\vert ^{2}}}d\psi &{\mbox{si }}z\in D\\f(z)&{\mbox{si }}z\in \partial D.\end{cases}}}$

La solución ${\displaystyle u}$ es continua en el disco unitario cerrado ${\displaystyle {\bar {D}}}$ y armónica sobre ${\displaystyle D.}$

El integrando se conoce como kernel de Poisson; esta solución resulta de la función de Green en dos dimensiones:

${\displaystyle G(z,x)=-{\frac {1}{2\pi }}\log \vert z-x\vert +\gamma (z,x)}$

donde ${\displaystyle \scriptstyle \gamma (z,x)}$ es armónica

${\displaystyle \Delta _{x}\gamma (z,x)=0\,}$

y elegida tal que ${\displaystyle \scriptstyle G(z,x)=0}$ para ${\displaystyle x\in \partial D}$.

Generalizaciones[editar]

Los problemas de Dirichlet son típicos de las ecuaciones en derivadas parciales elípticas, la teoría del potencial, y la ecuación de Laplace en particular. Otros ejemplos son la ecuación biarmónica y las ecuaciones relacionadas con la teoría de la elasticidad.

Este es uno de los problemas de varios tipos de clases problemas de EDP definidos por la información dada en el contorno, entre los cuales están también el problema de Neumann y el problema de Cauchy.

Aplicaciones[editar]

El problema de Dirichlet ocurre en múltiples problemas físicos:

1. En teoría del potencial para regiones desprovistas de carga.
2. En teoría de la elasticidad cuando no aparecen densidades de fuerza.

Para encontrar una función armónica que sea regular en un dominio y que coincida con una función continua dada en el límite de . El problema de encontrar la solución de una ecuación elíptica de segundo orden que es regular en el dominio también se conoce como Dirichlet o primer problema de valor de límite. Los problemas relacionados con esta tarea fueron estudiados desde 1840 por CF Gauss y luego por PGL Dirichlet [1] .

La solución del problema de Dirichlet para un dominio con un límite suficientemente suave se puede representar mediante la fórmula integral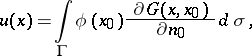

(1)

donde se encuentra la derivada en la dirección de la normal interior en el punto de la función Verde  , que se caracteriza por las siguientes propiedades:

1) si , o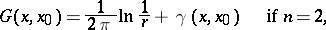

donde está la distancia entre los puntos y , es el área de superficie de la esfera de la unidad , es una función armónica regular tanto con respecto a la coordenada como con respecto a la coordenada ;

2) para , .

Para la esfera, la mitad del espacio y algunos otros dominios más simples, la función Verde se construye explícitamente, y la fórmula (1) produce una solución efectiva del problema de Dirichlet. Las fórmulas así obtenidas para la esfera y el semiespacio se conocen como fórmulas de Poisson (cf. fórmula de Poisson ).

El problema de Dirichlet es uno de los problemas fundamentales en la teoría del potencial . Ha servido, hasta el día de hoy, como una piedra de toque para los nuevos métodos que se están desarrollando y que luego contribuyen en mayor o menor medida a los avances en la teoría general de las ecuaciones diferenciales parciales.

Los siguientes métodos se emplean en el estudio del problema de Dirichlet.

El método variacional se basa en el hecho de que de todas las funciones definidas en y asumiendo valores dados , es una función armónica que minimiza la integral de Dirichlet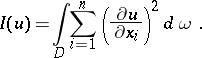

Se construye una secuencia de minimización especial , después de la cual se demuestra la convergencia. Dado que para la solución buscada del problema de Dirichlet se requiere la existencia de la integral , el método variacional es aplicable solo a las funciones que son trazas de funciones definidas para las cuales existe y está limitada.

En el método de potenciales (cf. Potenciales, método de ) se busca la solución del problema de Dirichlet como el potencial de doble capa de una densidad desconocida definida en . Con la ayuda de las fórmulas de salto con respecto a esta densidad, se obtiene una ecuación de Fredholm, de la que se desprende la existencia de la solución del problema de Dirichlet, teniendo en cuenta que la singularidad de esta solución se desprende del principio máximo. Se supone que .

En el método de alternancia de Schwarz, uno considera dos dominios y con una intersección no vacía , de manera que se conoce una manera de resolver el problema de Dirichlet y por separado. Luego se lleva a cabo un proceso para encontrar la solución al problema de Dirichlet . Los límites y se supone que son suave por partes, y en todas las intersecciones puntos de con , tanto y se supone que son lisa y que corta en un ángulo distinto de cero. Secuencias de funciones armónicas regulares en y y se construyen condiciones satisfactorias de límites especiales; luego se muestra que estas secuencias convergen uniformemente y que sus límites coinciden en. La función de límite armónico es regular y es la solución buscada del problema de Dirichlet. El método de Schwarz puede emplearse para la unión o la intersección de cualquier número finito de dominios.

El método de balayage en la forma en que fue originalmente introducido por H. Poincaré en 1890 es aplicable a dominios que pueden ser agotados por un conjunto de esferas innumerables. El paso inicial en este método es la construcción del potencial de Newton que asume el valor especificado en el límite , después de lo cual el problema se reduce a reemplazar este potencial por un potencial de masas ubicadas en sin cambiar los valores de on , es decir, a balayage de masas. Dicho proceso de balayage para la esfera se realiza fácilmente de manera explícita utilizando la fórmula de Poisson. El número innumerable de balayages de esferas cuya unión agota el dominio.De forma general produce un cierto potencial de masas ubicadas en el límite , y por lo tanto también la solución del problema de Dirichlet.

El método de Perron (o el método de las funciones superior e inferior), que es aplicable a dominios de un tipo bastante general, se asemeja al método de balayage. Implica la construcción de secuencias de funciones superior (superarmónica) e inferior (subarmónica), cuyo límite común es la solución buscada del problema de Dirichlet. Para que esta solución asuma un valor específico en un punto , es necesario y suficiente que exista una barrera local . La función es continua y superarmónica en la intersección (donde hay una esfera con su centro en el punto ); En todas partes excepto en el punto , donde desaparece.

Los puntos para los cuales existe una barrera local se conocen como puntos regulares. Si se compone exclusivamente de puntos regulares, la solución del problema de Dirichlet obtenida es continua y asume los valores especificados . Sin embargo, también pueden existir puntos irregulares en . Por ejemplo, los puntos aislados serán irregulares , mientras que la punta de una cúspide lo suficientemente delgada, al entrar , será irregular . Una consecuencia de la presencia de puntos irregulares es que el problema de Dirichlet no es resoluble para todas las funciones continuas en o bien que la solución es inestable con respecto a los cambios en los datos de contorno [6] .

Un método de solución generalizada del problema de Dirichlet, introducido en 1924 por N. Wiener, satisface las siguientes condiciones: a) es aplicable a todos los dominios; y b) produce la solución clásica del problema de Dirichlet si tal solución existe. Deje que un dominio sea ​​el límite de una secuencia creciente monótona de dominios regulares de tal manera que cualquier conjunto compacto esté contenido en if . La solución generalizada del problema de Dirichlet se obtiene como el límite de la secuencia de soluciones del problema de Dirichlet para los dominios y una función de límite continuamente extendida en el interior . La solución es independiente de la elección de la secuencia agotadora.Y de la manera de prolongación continua del interior .

Una solución generalizada del problema de Dirichlet también puede basarse en el método de Perron. Sea la envoltura inferior de la familia de todas las funciones superarmónicas que satisfacen la condición.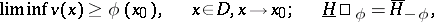

en . La desigualdad se aplica a todos los dominios y funciones . Si , la función es armónica. Se conoce como la solución generalizada del problema de Dirichlet, mientras que la función de límite se llama resolutiva. Cualquier función continua es resolutiva, y el comportamiento de la solución generalizada en un punto dependerá de si es regular o irregular.

La solución generalizada de Wiener del problema de Dirichlet satisface una representación integral (fórmula de la Vallée-Poussin):

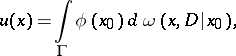(2)

que es la generalización de la fórmula (1). Aquí, es la medida armónica de un conjunto en un punto  [5] .

De ello se deduce que es posible considerar el problema generalizado de Dirichlet para funciones de límites arbitrarios , y la condición de los límites debe cumplirse solo en alguna forma más débil. Por ejemplo, si es un dominio con un límite suficientemente suave y si la función de límite tiene solo puntos de discontinuidad del primer tipo, la condición de límite debe cumplirse solo en los puntos de continuidad ; la solución debe estar limitada en los puntos de discontinuidad para garantizar la singularidad de la solución. NN Luzin generalizar el problema de Dirichlet para una función de límite medible casi todas partes finita arbitraria en . Una posible condición de límite sería para los valores de límite de la solución a lo largo de lo normal aexistir y coincidir con casi en todas partes .

El problema de Dirichlet para la ecuación elíptica general de segundo orden

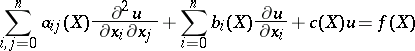(3)

Es un problema de Fredholm. La solución buscada debe ser regular en el dominio y debe asumir valores dados en el límite. Los métodos anteriores para estudiar el problema de Dirichlet para funciones armónicas también se han generalizado a la ecuación (3).

Para sistemas elípticos uniformes, el problema de Dirichlet puede no ser un problema que no sea de Fredholm, sino que puede tener infinitas soluciones lineales independientes [8] .

El problema de Dirichlet también se estudia para ciertas ecuaciones no elípticas o ecuaciones degeneradas. En tales casos, el problema de Dirichlet a veces resulta mal planteado.