Magnitudes meteorológicas, climatológicas y atmosféricas
El índice xerotérmico es una sencilla fórmula que sirve para determinar, dentro de los climas intertropicales, los límites entre las precipitaciones de los meses secos y las de los meses lluviosos. Fue diseñado por Henri Gaussen, meteorólogo francés, para considerar, además del monto pluviométrico mensual, la mayor o menor temperatura media de ese mes, la cual incidirá, naturalmente, sobre la mayor o menor evaporación también en dicho mes.
Concepto
Etimológicamente el concepto xerotérmico viene de "xeros", que significa sequedad, y térmico, temperatura. Su cálculo es muy sencillo ya que para saber si el monto pluviométrico de un mes se debe considerar como el de un mes seco o lluvioso basta con multiplicar por 2 el valor de la temperatura media de ese mes lo cual nos dará una cifra que, considerada en mm de precipitación nos servirá para determinar si es seco (cuando la cifra es inferior al promedio de las lluvias en ese mes) o si es lluvioso, en caso de que el resultado sea superior a dicho monto (1 ).
Algunos ejemplos
- Datos climáticos de Santa Elena de Uairén (Estado Bolívar, en la Guayana Venezolana):
- a) Localización: latitud 4º 36' N, longitud 61º 06' W, altitud, 910 msnm.
- b) Temperaturas: enero (21,6º C), febrero (22º C), marzo (22,5º C), abril (22,3º C), mayo (22º C), junio (21,5º C), julio (21,5º C), agosto (21,5º C), septiembre (22º C), octubre (22,1º C), noviembre (22º C), diciembre (21,8º C). Temperatura media anual: 21,8º C.
- c) Precipitaciones: enero (72 mm), febrero (83 mm), marzo (92 mm), abril (134 mm), mayo (248 mm), junio (251 mm), julio (219 mm), agosto (171 mm), septiembre (116 mm), octubre (102 mm), noviembre (119 mm), diciembre (132 mm). Monto pluviométrico anual: 1739 mm
- a) Localización: latitud 8º 44' N., longitud 70º 55' W., altitud: 2980 msnm.
- b) Temperaturas: enero (10,1º C), febrero (11,2º C), marzo (11,6º C), abril (11,7º C), mayo (11,8º C), junio (11º C), julio (10,4º C), agosto (10,8º C), septiembre (11º C), octubre (10,9º C), noviembre (10,4º C), diciembre (10,5º C). Temperatura media anual: 11º C.
- c) Precipitaciones: enero (7 mm), febrero (12 mm), marzo (29 mm), abril (80 mm), mayo (106 mm), junio (97 mm), julio (104 mm), agosto (82 mm), septiembre (69 mm), octubre (68 mm), noviembre (30 mm), diciembre (10 mm). Monto pluviométrico anual: 694 mm
- Datos climáticos de Mene Grande (Estado Zulia, Venezuela):
- a) Localización: latitud 9º 49' N, longitud 70º 56' W, altitud: 18 msnm
- b) Temperaturas: enero (26,4º C), febrero (26,8º C), marzo (27,4º C), abril (27,1º C), mayo (27,1º C), junio (27,1º C), julio (27,2º C), agosto (27,4º C), septiembre (27,2º C), octubre (26,3º C), noviembre (26,2º C), diciembre (26,1º C). Temperatura media anual: 26,9º C.
- c) Precipitaciones: enero (45 mm), febrero (23,8 mm), marzo (41 mm), abril (118 mm), mayo (186 mm), junio (142 mm), julio (63 mm), agosto (93 mm), septiembre (128 mm), octubre (240 mm), noviembre (136 mm), diciembre (123 mm). Monto pluviométrico anual: 1310 mm
Análisis
Muchos geógrafos ya se habían manifestado sobre la necesidad de diferenciar los climas secos de los húmedos. Así por ejemplo, en Venezuela y en otros países de la zona intertropical se venía empleando un monto fijo mensual de 50 ó 60 mm de precipitación (según diversos autores) para diferenciar los meses secos, con una precipitación mensual inferior a esta cifra, y los lluviosos, cuando es superior a ella. Pero este dato empírico impide emplear la cifra cuando las diferencias de altura entre dos estaciones son lo suficientemente grandes como para alterar la efectividad de las lluvias, debido a la menor evaporación que está determinada por el aumento de la altitud sobre el nivel del mar y, por ende, por la disminución de la temperatura. Cuando en una misma cuenca hidrográfica, por ejemplo, la cuenca del Orinoco, existen lugares ubicados a distintas alturas (desde más de 5000 metros sobre el nivel del mar en la Cordillera Oriental de Colombia, hasta la misma orilla del Atlántico, pasando por las mesetas o tepuyes, a más de 2500 msnm) y estamos estudiando el clima de estos lugares resulta muy útil el empleo del índice xerotérmico de Gaussen, el cual nos permite hacer comparaciones en las que se minimiza el efecto de la altitud sobre la evaporación al tomar en cuenta la temperatura, que ya determina en gran parte esa evaporación. El ejemplo de los datos climatológicos de Santa Elena de Uairén, por ejemplo, nos demuestra que no existe allí ningún mes seco, lo cual parece contradecir el hecho de que a esta población se le considera la capital de La Gran Sabana, ya que, a pesar de que muchos autores han identificado el clima de esta región del sudeste de Venezuela como, precisamente, clima de sabana, ello no es correcto, ya que el hecho de que su vegetación sea de sabana no se debe al clima sino más bien a la naturaleza arenosa y areniscosa de los suelos, tal como se indica en el artículo respectivo.
Si analizamos los datos climáticos indicados arriba, que corresponden a climas isotermos de la zona intertropical, pero de poblaciones ubicadas a distintas alturas, podremos ver en la práctica la aplicación de la fórmula ideada por Gaussen:
- Ningún mes en Santa Elena de Uairén podría considerarse como seco ya que en todos los casos, el monto pluviométrico en mm es bastante superior al doble de la temperatura en grados centígrados para dicho mes. Por ello es que no se explica la presencia de una vegetación de sabana si el clima es de selva, por lo que los motivos son otros, como ya se ha indicado.
- En el caso de Mucuchíes podemos ver la forma como incide la mayor altitud sobre las temperaturas medias mensuales. Si usáramos los montos pluviométricos de 50 ó 60 mm de lluvia mensual como umbral entre los meses secos y lluviosos, tal como se indica arriba (como se hacía antes), el mes de marzo en Mucuchíes sería un mes seco. Sin embargo, con una temperatura media de 11,6 °C, un monto pluviométrico de 29 mm es más del doble de dicho umbral (el doble de 11,6 es 23,2 mm, cifra que daría una idea más acertada del verdadero umbral que deberíamos considerar en este caso) por lo que, según el índice de Gaussen, tampoco sería un mes seco.
- Y en el caso de Mene Grande, población ubicada en la parte oriental del estado Zulia, la comparación con Mucuchíes nos explica perfectamente la utilidad del empleo del índice xerotérmico de Gaussen: como hemos visto, el mes de marzo en Mucuchíes es un mes lluvioso a pesar de que sólo recibe unos 29 mm de precipitaciones. En cambio, una cifra bastante mayor de 41 mm en el mismo mes en Mene Grande corresponderían a un mes seco por ser su temperatura mucho más elevada, lo que hace que la evaporación sea también mucho mayor.
La fórmula de Köppen
La clasificación climática de Köppen también considera un umbral de separación entre los climas Aw (estación seca correspondiente con la época de sol bajo o invierno hemisférico) y los climas áridos (Climas B). Expresada en valores de la escala °C (Celsius) sería
- r = 2 (T + 14)
en la que r representa el umbral en cm de precipitación anual, y T la temperatura media anual en la escala C. Ello significa que si el resultado obtenido al aplicar dicha fórmula es igual o menor que el monto pluviométrico anual en cm, el clima será árido y de sabana en caso contrario. Por ejemplo, en el caso de Barcelona (Venezuela), cuya lluviosidad anual es de 608 mm (es decir, 60,8 cm) y la temperatura media anual es de 26,9 °C, dicho umbral sería de 2 (26,9 + 14), es decir, 81,8 cm (818 mm), por lo que el clima de dicha ciudad sería, evidentemente, un clima semiárido (Bsi, en la clasificación de Köppen) y no un clima Aw. Así, al comparar las dos fórmulas, la de Köppen y la de Gaussen, vemos que con la segunda se alcanza una mayor precisión al poder establecer individualmente la fórmula para cada mes en particular.
Y Arthur Newell Strahler, en su famoso libro sobre Geografía Física (2ª edición en inglés de 1960) desarrolla en los gráficos climáticos del mismo, un ingenioso método para diferenciar los meses lluviosos de los secos en las estaciones meteorológicas ubicadas en la zona intertropical: los meses secos están identificados con un icono que señala unas isobaras que encierran la letra H (High) es decir, indicando los meses con una situación anticiclónica definida como subtropical high (altas presiones subtropicales); mientras que los meses lluviosos están señalados con otro icono que habla de equatorial trough término correspondiente al de cinturón de bajas presiones ecuatoriales y que recientemente tomó el nombre de zona de convergencia intertropical. Así pues, no se trata de tomar una mayor o menor precipitación como umbral para diferenciar los meses secos de los lluviosos sino elaborar el gráfico primero e identificar en el mismo la causa determinante de las diferencias estacionales de los climas intertropicales, excluyendo el clima de selva ecuatorial en el que la precipitación es más homogénea a lo largo del año (2 ).
Crítica
El índice xerotérmico descrito por Gaussen introduce una mejora importante en los criterios de clasificación climática de la Zona Intertropical especialmente útil a la hora de elaborar mapas climatológicos. Si observamos un mapa climático de África desde el ecuador hasta el Trópico de Cáncer, notaremos una distribución en fajas extendidas en el sentido de la latitud, en las que la sequedad del clima, medida en la cantidad de meses secos a lo largo del año, va progresando hacia el norte, desde ningún mes seco en el ecuador hasta ningún mes lluvioso en el Trópico de Cáncer.
La zona de transición entre los climas de sabana y los áridos se conoce en el continente africano con el nombre de Sahel. Esta nitidez en la distribución geográfica de los distintos tipos climáticos se debe a que en este caso, el relieve no introduce modificaciones importantes en el clima por estar constituido por plataformas realzadas y superficies de erosión bastante homogéneas en cuanto a su altitud sobre el nivel del mar se refiere (tal vez con la excepción de algunas mesetas más elevadas del África Oriental, en Kenia, Etiopía y otros países). Es por ello que, en este caso, la aplicación del índice xerotérmico en la delimitación de los distintos tipos de clima, casi no tendría ninguna importancia o diferencia a la de emplear otros criterios tradicionalmente aceptados. Pero en el caso de América del Sur y la región del Caribe, donde el relieve introduce un factor importante de modificación climática, resulta mucho más conveniente su empleo con el fin de afinar esa elaboración de los mapas climáticos.
Por otra parte, cuando tenemos en cuenta la respuesta de la naturaleza de la zona intertropical a las variaciones y fronteras climáticas, nos daremos cuenta de que la matización introducida por el empleo del índice xerotérmico de los tipos climáticos, no es muy relevante. Por ejemplo, muchas especies vegetales tienen un poder de adaptación muy grande en lo que se refiere a las diferencias establecidas por las fronteras climáticas y este tema está más relacionado con la Ecología que con la propiaClimatología. El ejemplo de la floración de algunas especies vegetales de la zona intertropical al final de la época de sequía nos asombra anualmente en una especie de milagro de la naturaleza en esta zona geoastronómica. Y el almacenamiento de agua después de casi seis meses de sequía absoluta es casi un fenómeno inexplicable en el caso de algunos árboles, como en el caso del mango (Mangifera indica), árbol cuya enorme producción de frutos se presenta en su apogeo durante el mes de mayo en el hemisferio norte, que es el momento en que finaliza la época de sequía en las latitudes intertropicales de este hemisferio. La explicación de esta aparente paradoja es muy sencilla: este árbol está adaptado a un clima de la zona subtropical de clima monzónico (en la India, de donde viene su nombre), que es mucho más extremado que el que conseguimos más al sur en la zona de sabana, por lo que su adaptación ecológica a una época de sequía prolongada es mucho mayor que la que se necesitaría en esta zona de clima de sabana. Más bien sucede una especie de paradoja: los años en que se han presentado algunas lluvias bastante persistentes y abundantes en la época de sequía en estas zonas de clima Aw (como efectos de las vaguadas asociadas a los anticiclones, los cuales se deben, a su vez, a las temperaturas frías del invierno boreal), la producción y calidad de la cosecha de mangos bajan considerablemente.
En resumen, existen diversos sistemas o fórmulas para establecer una clasificación climática que nos permita lograr una mayor o menor precisión en cuanto a la delimitación sobre el mapa de los distintos tipos climáticos en la zona intertropical. Y los cuatro que se han indicado aquí (50 mm, 60 mm, la fórmula de Gaussen y la de Köppen) para establecer los límites o umbrales de separación entre los climas Af y Aw por un lado, y Aw y Bsi por el otro, resultan plenamente válidos dependiendo únicamente de la mayor o menor exactitud que tengamos en cuenta al recopilar y analizar los datos meteorológicos.
La insolación es la cantidad de energía en forma de radiación solar que llega a un lugar de la Tierra en un día concreto (insolación diurna) o en un año (insolación anual).
Puede calcularse asumiendo que no hay atmósfera o que se mide en la parte alta de la atmósfera y se denominainsolación diurna o anual no atenuada o que se mide en la superficie de la Tierra para lo cual hay que tener presente la atmósfera y que en este caso se denomina atenuada siendo su cálculo mucho más complejo.
Supongamos un instante t de ese día con el Sol a una altura h sobre el horizonte. El Sol está tan lejos que sus rayos son prácticamente paralelos. Si tenemos una superficie S' fija sobre la superficie de la Tierra en el plano del horizonte y queremos saber que energía del Sol llegará a ésta superficie. Sea S la superficie perpendicular al haz de luz necesario para iluminar S'. La superficie de S variará según la altura del Sol. Si h=90º entonces S=S'. Las dos superficies forman un ángulo 90-h=z la distancia cenital. Por tanto sus áreas cumplen  . A este fenómeno se le denomina Ley del coseno de Lambert y causa que en las regiones ecuatoriales donde los rayos solares caen más perpendiculares haga más calor que en las polares donde los rayos son muy oblicuos.
. A este fenómeno se le denomina Ley del coseno de Lambert y causa que en las regiones ecuatoriales donde los rayos solares caen más perpendiculares haga más calor que en las polares donde los rayos son muy oblicuos.
 . A este fenómeno se le denomina Ley del coseno de Lambert y causa que en las regiones ecuatoriales donde los rayos solares caen más perpendiculares haga más calor que en las polares donde los rayos son muy oblicuos.
. A este fenómeno se le denomina Ley del coseno de Lambert y causa que en las regiones ecuatoriales donde los rayos solares caen más perpendiculares haga más calor que en las polares donde los rayos son muy oblicuos.
Por lo que el incremento de insolación que llega a la superficie s' en un incremento de t vale:
Dónde la altura del Sol cumple:
Dónde H es el ángulo horario del Sol.
Para hallar la energía total I que llega a la Tierra por unidad de área en un día habrá que hacer la suma:
La duración del día, prescindiendo de la refracción astronómica es  comenzando el día con un ángulo horario
comenzando el día con un ángulo horario 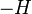 y acabando con un ángulo horario
y acabando con un ángulo horario 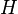 que cumple:
que cumple:
 comenzando el día con un ángulo horario
comenzando el día con un ángulo horario 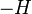 y acabando con un ángulo horario
y acabando con un ángulo horario 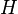 que cumple:
que cumple:
Por lo que la insolación valdrá:
donde la integral es inmediata:
Por lo que la insolación diurna no atenuada vale:
Siendo

Las unidades para calcular la insolación en ésta expresión
Si expresamos y la Insolación I en langleys, el primer sumando habrá que multiplicarlo por
y la Insolación I en langleys, el primer sumando habrá que multiplicarlo por  pues un día tiene 1440 minutos. El segundo sumando si expresamos H en grados sexagesimales habrá que mutlplicarlo por 4 ya que los grados dividido por 15 son horas y luego hay que multiplicar por 60 para pasar a minutos. Así que en plan práctico:Siendo
pues un día tiene 1440 minutos. El segundo sumando si expresamos H en grados sexagesimales habrá que mutlplicarlo por 4 ya que los grados dividido por 15 son horas y luego hay que multiplicar por 60 para pasar a minutos. Así que en plan práctico:Siendo- También se puede expresar H en radianes y multiplicar los dos sumandos por

Otra fórmula para la Insolación diurna
Si la expresión anterior la dividimos por resulta:Siendo
resulta:Siendo- Si expresamos H en radianes faltaría multiplicar por
 para obtener la insolación en langleys.
para obtener la insolación en langleys.
Aplicación práctica
- Un lugar a 30º N de latitud recibe el 21 de junio, el día del solsticio de verano una insolación de 988,17 langleys/día y el 21 de diciembre, día del solsticio de invierno sólo 472,51 langleys/día.
- En el ecuador en el 21 de junio, la insolación es 800,87 langleys/día.
- Un lugar a 30º S de latitud recibe el 21 de junio, el día del solsticio de invierno una insolación de 442,68 langleys/día. La diferencia a una misma latitud entre el hemisferio norte y sur radica en que el 21 de diciembre la Tierra está cerca del perihelio y recibe más insolación que el 21 de junio que está cerca del afelio.
La insolación en lugares con día permanente
La expresión:indica el valor del arco semidiurno H en el momento del orto u ocaso y no tiene sentido en aquellos valores donde donde el día es permanente o la noche es permanente (
donde el día es permanente o la noche es permanente ( ).En el primer caso H=12 h con lo que la insolación queda:Siendo
).En el primer caso H=12 h con lo que la insolación queda:SiendoEjemplos
Calcular la insolación diurna en la parte alta de la atmósfera en el solsticio de verano el polo norte y sur.- El solsticio de verano en el polo norte ocurre el 21 de junio cuando la distancia entre el Sol y la Tierra es 1,0163 U.A. así que I=1090,97 langleys.
- El solsticio de verano en el polo sur ocurre el 21 de diciembre cuando la distancia entre el Sol y la Tierra es 0,9837 U.A. así que I=1164,48 langleys.
En el solsticio de verano el polo norte recibe en la parte superior de la atmósfera más insolación que el Ecuador y en el polo sur el efecto es todavía mayor, por estar la Tierra más cerca del Sol.Esto está reñido con la experiencia. Las temperaturas más altas no ocurren en el verano polar sino en los trópicos. A nivel de la superficie terrestre no es así y la explicación es fácil: los rayos solares durante el día permanente aparecen muy inclinados, atraviesan mucha atmósfera y son más absorbidos, además, la nieve, hielo ynubes hacen que el albedo sea mucho mayor en el polo que en las regiones ecuatoriales y una gran parte de la radiación incidente es reflejada.Tabla y gráfica de valores de la insolación no atenuada
Fecha 22 Dic. 4 Feb. 21 Mar. 6 May. 22 Jun. Declinación Sol -26º 26' -16º 23' 0º +16º 22' +23º 26' r (U.A.) 0,9837 0,9857 0,9960 1,0087 1,0163 La declinación solar y la distancia entre la Tierra y el Sol para unas fechas concretas Aplicando las fórmulas anteriores se obtiene para la insolación diurna no atenuada los valores en langleys:Hemisferio Norte Ecuador Hemisferio Sur Fecha 90 70 50 30 0 -30 -50 -70 -90 22-dic 0,00 0,00 178,60 472,51 854,83 1054,75 1070,64 1094,25 1164,48 04-feb 0,00 24,44 292,81 576,57 890,28 987,71 922,71 797,13 822,28 21-mar 0,00 310,85 584,21 787,10 908,86 787,10 584,21 310,85 0,00 06-may 793,85 769,75 891,36 954,34 860,42 557,42 283,24 23,78 0,00 22-jun 1090,97 1025,18 1003,06 988,17 800,87 442,68 167,33 0,00 0,00 La radiación solar anual no atenuada
Para cada latitud lo único que hay que hacer es calcular la insolación diaria no atenuada y hacer la suma para todos los días del año. Distinguiremos entre el hemisferio norte y sur.Latitud 90 º 80 º 70 º 60 º 50 º 40 º 30 º 20 º 10 º 0 º H. Norte 129,25 133,74 148,02 178,17 214,63 248,39 276,66 297,88 311,08 315,72 H. Sur 132,33 136,77 150,91 180,83 216,98 250,36 278,17 298,90 311,62 315,72 La insolación anual no atenuada expresada en Kilolangleys = 1000 langleys La radiación solar diurna en la superficie de la Tierra
Radiación solar atenuada en un instante dado
La radiación solar recibida por la superficie de la Tierra está atenuada, respecto a la que llega a la parte alta de la atmósfera, por distintos procesos que se producen en su recorrido por la atmósfera. Estos procesos son:- La atmósfera absorbe la radiación solar selectivamente especialmente el vapor de agua y el ozono que impide pasar toda radiación de longitud de onda inferior a 0,29 micras.
- La difusión molecular o de Rayleigh debida a los gases atmosféricos y al vapor de agua.
- La difusión y absorción por aerosoles o turbidez.
Vamos a suponer la ausencia de nubes, un fenómeno local que resulta imprevisible.Los tres procesos citados atenúan la intensidad de la radiación solar cumpliendo la ley de Beer selectiva para cada longitud de onda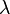 . Sea un haz monocromático de intensidad
. Sea un haz monocromático de intensidad  que penetra en un medio homogéneo. Tras atravesar un
que penetra en un medio homogéneo. Tras atravesar un  parte de la radiación es absorbida:
parte de la radiación es absorbida: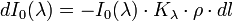 donde
donde  es el coeficiente de absorción que es una función compleja de la longitud de onda y que al tratarse de un medio gaseoso como la atmósfera depende, aparte de su composición, de la presión y la temperatura.
es el coeficiente de absorción que es una función compleja de la longitud de onda y que al tratarse de un medio gaseoso como la atmósfera depende, aparte de su composición, de la presión y la temperatura.  es la densidad de la atmósfera.Por integración a lo largo del espesor atravesado:
es la densidad de la atmósfera.Por integración a lo largo del espesor atravesado: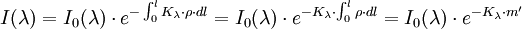 siendo
siendo 
 la masa absorbente por unidad de superficie, contenida a lo largo del recorrido del haz.
la masa absorbente por unidad de superficie, contenida a lo largo del recorrido del haz.
La atenuación depende fuertemente del camino recorrido por el rayo de luz en la atmósfera y que es mínimo para una distancia cenital y máximo para un rayo incidiendo por el plano horizontal
y máximo para un rayo incidiendo por el plano horizontal 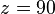 . Si el haz atraviesa un medio como la atmósfera que puede considerarse estratificado horizontalmente, esto es que el valor de sus propiedades depende exclusivamente de su altura h sobre el nivel del mar y consideramos que el rayo tiene una trayectoria recta, cumplirá:
. Si el haz atraviesa un medio como la atmósfera que puede considerarse estratificado horizontalmente, esto es que el valor de sus propiedades depende exclusivamente de su altura h sobre el nivel del mar y consideramos que el rayo tiene una trayectoria recta, cumplirá: por lo que:
por lo que: 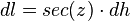 Así que la insolación atenuada para un rayo con distancia cenital z vale:
Así que la insolación atenuada para un rayo con distancia cenital z vale: siendo
siendo 
 la masa absorbente por unidad de superficie, de una columna vertical de atmósfera entre las alturas h1 y h2. A esta cantidad se llamaespesor óptico de la capa.
la masa absorbente por unidad de superficie, de una columna vertical de atmósfera entre las alturas h1 y h2. A esta cantidad se llamaespesor óptico de la capa.
Al igual que definimos el coeficiente de absorción, se puede definir
el coeficiente de absorción, se puede definir  y
y  como los coeficientes de difusión y turbidez, se verificará:donde m es el espesor óptico que a nivel del mar se supone que m=1, y z la distancia zenital de la radiación.Integrando para todo el espectro electromagnético:En lugar de las exponenciales se pueden considerar unos factores medios
como los coeficientes de difusión y turbidez, se verificará:donde m es el espesor óptico que a nivel del mar se supone que m=1, y z la distancia zenital de la radiación.Integrando para todo el espectro electromagnético:En lugar de las exponenciales se pueden considerar unos factores medios

 así que:donde
así que:donde es producto de los valores medios de los tres coeficientes de absorción, difusión y turbidez y se toma en los cálculos un valor de a=0,7
es producto de los valores medios de los tres coeficientes de absorción, difusión y turbidez y se toma en los cálculos un valor de a=0,7
mientras es la radiación solar no atenuada.
es la radiación solar no atenuada.La radiación solar diurna atenuada
Supongamos un instante t del día donde queremos calcular la radiación que llega a la superficie de la Tierra, con el Sol a una altura h sobre el horizonte.Supondremos que no hay nubes y que toda la radiación solar atenuada por los procesos descritos anteriormente llega a la superficie.Si tenemos una superficie S' fija sobre la superficie de la Tierra en el plano del horizonte y queremos saber que energía del Sol llegará a ésta superficie. Sea S la superficie perpendicular al haz de luz necesario para iluminar S'. La superficie de S variará según la altura del Sol. Las dos superficies forman un ángulo 90-h=z ladistancia cenital. Por tanto sus áreas cumplen S=S'cos z. Por lo que el incremento de insolación que llega a la superficie S' en un incremento de t vale:donde la altura del Sol cumple:donde H es el ángulo horario del Sol.Para hallar la energía total I que llega a la Tierra por unidad de área en un día habrá que hacer la suma:La duración del día, prescindiendo de la refracción astronómica es comenzando el día con un ángulo horario
comenzando el día con un ángulo horario 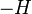 y acabando con un ángulo horario
y acabando con un ángulo horario 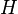 que cumple:por lo que la insolación diurna atenuada valdrá:donde supondremos a=0,7.Para calcular la integral de forma aproximada aplicaremos el método de Simpson.Si expresamos
que cumple:por lo que la insolación diurna atenuada valdrá:donde supondremos a=0,7.Para calcular la integral de forma aproximada aplicaremos el método de Simpson.Si expresamos y H en radianes, hay que multiplicar por
y H en radianes, hay que multiplicar por  para que la Insolación I aparezca en langleys.
para que la Insolación I aparezca en langleys.Ejemplos
- Calcular la insolación diurna superficial el día del solsticio de verano en el polo norte cuando Ds=23,44º y r=1,0163 U.A.. Resulta una insolación de 445,0 langleys. Observar que ese día y en el polo norte la insolación no atenuada vale 1090,9 langleys por lo que sólo llega a la superficie el 40,8 % de la radiación incidente.
- Comparar la insolación en la parte superior de la atmósfera y en la superficie a distintas latitudes el día del solsticio de verano en el hemisferio norte (21 de junio)
Hemisferio Sur Ecuador Hemisferio Norte Latitud -66,5 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 No atenuada 0 47,50 167,31 303,92 442,68 575,36 696,24 800,87 885,68 948,48 988,17 1005,15 1003,06 992,25 1025,18 1074,33 1090,97 Atenuada 0 1,19 34,50 107,25 199,05 295,62 387,47 467,79 531,61 575,39 596,88 595,15 570,85 527,03 473,59 447,92 445,00 La radiación solar anual directa en la superficie de la Tierra
Para cada latitud lo único que hay que hacer es calcular la insolación diaria atenuada directa y hacer la suma para todos los días del año. Distinguiremos entre el hemisferio norte y sur.Latitud 90 º 80 º 70 º 60 º 50 º 40 º 30 º 20 º 10 º 0 º H. Norte 39,95 44,89 68,87 80,46 105,94 132,07 155,24 173,18 184,52 188,53 H. Sur 40,98 46,00 60,63 81,98 107,48 133,46 156,37 173,97 184,94 188,53 La insolación anual atenuada expresada en Kilolangleys = 1000 langleys La radiación absorbida por la superficie de la Tierra
El cálculo efectuado anteriormente se refiere a la energía solar directa de onda corta que llega a la superficie de la Tierra tras sufrir los procesos de absorción y difusión por los gases de la atmósfera. Sin embargo a la superficie de la Tierra llega más energía:- Las nubes dispersan en promedio el 50% de la energía solar de la un 23% llega indirectamente a la Tierra como onda corta.
- La difusión por la atmósfera disminuye la insolación directa, pero esa energía absorbida por el aire es reemitida en parte hacia la superficie de la Tierra donde es absorbida.
- La Tierra como cuerpo caliente (en promedio a unos 15 °C) emite hacia la atmósfera una radiación de onda larga que en promedio es de unos 410 W/m2 de ella unos 40 W/m2 escapan directamente al espacio siendo el resto absorbido por los gases de efecto invernadero de la atmósfera, en promedio 361 W/m2 vuelven a la superficie terrestre en forma de onda larga calentando su superficie, este hecho se denomina efecto invernadero.
La radiación absorbida por el sistema Tierra-atmósfera
Si queremos saber la energía absorbida tanto por la Tierra como por la atmósfera habrá que sumar a la energía absorbida por la Tierra:- La energía solar de onda corta absorbida por el aire que en promedio representa unos 58 W/m2
- La energía absorbida por las nubes, que es muy pequeña, del orden de 7 W/m2, ya que las nubes lo que fundamentalmente hacen es dispersar la radiación tanto hacia el espacio como hacia la Tierra.



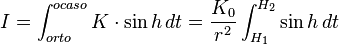


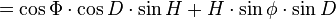














No hay comentarios:
Publicar un comentario