Magnitudes meteorológicas, climatológicas y atmosféricas
La constante solar es la cantidad de energía recibida en forma de radiación solar por unidad de tiempo y unidad de superficie, medida en la parte externa de la atmósfera terrestre en un plano perpendicular a los rayos del Sol. Los resultados de su medición por satélites arrojan un valor promedio de 1366 W/m2.
Para calcular la constante solar basta con dividir el flujo energético que emite el Sol por la relación de áreas entre la superficie del Sol (con  el radio solar) y la de una esfera de radio
el radio solar) y la de una esfera de radio  (una unidad astronómica) del mismo. Para obtener este valor, que en la práctica está medido por satélites, se debe usar como temperatura efectiva (
(una unidad astronómica) del mismo. Para obtener este valor, que en la práctica está medido por satélites, se debe usar como temperatura efectiva ( ) del Sol el valor 5776 K.
) del Sol el valor 5776 K.
 el radio solar) y la de una esfera de radio
el radio solar) y la de una esfera de radio  (una unidad astronómica) del mismo. Para obtener este valor, que en la práctica está medido por satélites, se debe usar como temperatura efectiva (
(una unidad astronómica) del mismo. Para obtener este valor, que en la práctica está medido por satélites, se debe usar como temperatura efectiva ( ) del Sol el valor 5776 K.
) del Sol el valor 5776 K.
Para la Tierra en su conjunto, dada su sección transversal de 127,4 millones de km2, la energía es del orden de 1,74 × 1017 W. En realidad la «constante solar» no es propiamente una constante, pero sí un parámetro que a corto y medio plazo varía dentro de márgenes estrechos.
Otras unidades de la constante solar
La constante solar se puede expresar en 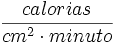 . Para ello hay que recordar 1 julio = 0,24 calorías, 1 minuto = 60 s y 1 m2 = 104 cm2
. Para ello hay que recordar 1 julio = 0,24 calorías, 1 minuto = 60 s y 1 m2 = 104 cm2
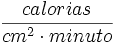 . Para ello hay que recordar 1 julio = 0,24 calorías, 1 minuto = 60 s y 1 m2 = 104 cm2
. Para ello hay que recordar 1 julio = 0,24 calorías, 1 minuto = 60 s y 1 m2 = 104 cm2 .
.
Una unidad muy utilizada para medir la energía que llega a la parte superior de la atmósfera en un día es:
Así un lugar a 30º N de latitud recibe el 21 de junio, el día del solsticio de verano una insolación de 1004,7 langleys/día y el 21 de diciembre, día del solsticio de invierno sólo 480,4 langleys/día.
Por otra parte se puede calcular la insolación anual en la parte alta de la atmósfera a diferentes latitudes. Para el polo la insolación anual es 133,2 kilolangleys/año mientras en el ecuador asciende a 320,9 kilolangleys/año donde el klangley=1000 langleys.
Luminosidad solar
Se llama luminosidad solar a la energía emitida por el Sol en la unidad de tiempo. Por tanto vale:
 .
.
Análogo resultado se obtiene en vez de hacer el cálculo para la superficie solar, hacerlo a la distancia de la Tierra y usar la constante solar. El flujo emitido por el Solva disminuyendo con la distancia debido a que se reparte por una superficie mayor. La superficie esférica a la distancia en que se encuentra la Tierra vale:
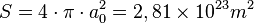 .
.
La luminosidad solar vale por tanto:
Análogo resultado se obtiene haciendo el cálculo mediante el siguiente razonamiento:
El diámetro angular de la Tierra vista desde el Sol es de aproximadamente 1/11.700 de radián, así que el ángulo sólido de la Tierra desde el Sol es de 1/175.000.000estereorradianes. Eso implica que la Tierra intercepta sólo una parte entre 2000 millones de la radiación que el Sol emite (aproximadamente 3,6×1026 W).
La constante solar incluye todos los tipos de radiación, no sólo la visible. La constante solar está relacionada con la magnitud aparente del Sol (la intensidad de su brillo según lo recibe el espectador) cuyo valor es de −26,8; ya que ambos parámetros vienen a describir el brillo observable del Sol, aunque la magnitud se refiere solamente al espectro visible.
Variación
La radiación emitida por el Sol no es exactamente constante, sino que sufre de fluctuaciones caóticas de muy pequeña amplitud y de oscilaciones periódicas descritas como ciclos de actividad, así como de variaciones tendenciales por las cuales el brillo del Sol ha ido creciendo lentamente a lo largo de su historia.
Las variaciones periódicas parecen consistir en varias oscilaciones de período (duración) diferente, de las que la más conocida es la de 11 años que se manifiesta como ciclo de variación de la abundancia de manchas solares en la fotosfera. Los ciclos recientes muestran una variación del brillo solar dentro de los límites de un 0,1%; sin embargo desde el mínimo de Maunder, una época sin manchas entre 1650 y 1700, la radiación solar podría haber crecido hasta en un 0,6%.
Los modelos teóricos del desarrollo del Sol implican que hace unos 3.000 millones de años, cuando el Sistema Solar sólo tenía un tercio de su edad, el Sol emitía sólo un 75% de la energía que emite actualmente. El clima de la Tierra era menos frío de lo que implica este dato, porque la composiciónn de la atmósfera era muy diferente, mucho más abundante en gases de invernadero, sobre todo dióxido de carbono (CO2) y amoniaco (NH3).
Otras variaciones de carácter cíclico tienen que ver con los parámetros orbitales de la Tierra, especialmente con la excentricidad. Ésta no afecta en sí a la energía media recibida a largo plazo, pero sí a las variaciones estacionales. Actualmente, la Tierra se encuentra en su perihelio a primeros de enero, coincidiendo casi con el solsticio de invierno, lo que contribuye a que el Hemisferio Norte recoja algo más de energía solar que el Sur. Pero la fecha del perihelio (y del afelio) oscila con un período muy largo.
En cualquier caso la excentricidad de la órbita terrestre es relativamente pequeña, pero es grande sin embargo en otros planetas, como Marte y sobre todo Plutón (ahora considerado «planeta enano»). En éstos la diferencia de energía interceptada en distintos momentos del año puede llegar a ser considerable. La tabla siguiente presenta las constantes solares de los planetas del Sistema solar, calculadas en función de su distancia media.
Relevancia
El valor de la constante solar, así como su relativa estabilidad, son fundamentales para muchos de los más importantes procesos terrestres. En particular, para la determinación del clima, los procesos geológicos externos, y para la vida. También para el futuro de la Humanidad, al menos en lo que éste dependa del desarrollo tecnológico de las energías renovables.
Constante solar para los distintos planetas
El flujo emitido por el Sol va disminuyendo con la distancia debido a que se reparte por una superficie mayor. Supongamos que llamamos  a la constante solar a la distancia de la Tierra (1 unidad astronómica) y K a la distancia r expresada en U.A. de cualquier planeta solar, se cumplirá que la luminosidad solar no cambia, es decir:
a la constante solar a la distancia de la Tierra (1 unidad astronómica) y K a la distancia r expresada en U.A. de cualquier planeta solar, se cumplirá que la luminosidad solar no cambia, es decir:
 a la constante solar a la distancia de la Tierra (1 unidad astronómica) y K a la distancia r expresada en U.A. de cualquier planeta solar, se cumplirá que la luminosidad solar no cambia, es decir:
a la constante solar a la distancia de la Tierra (1 unidad astronómica) y K a la distancia r expresada en U.A. de cualquier planeta solar, se cumplirá que la luminosidad solar no cambia, es decir:
es decir:
Supongamos por ejemplo el planeta Marte que dista 1,5236 U.A. la constante solar valdrá:
Temperatura efectiva en los distintos planetas
Para calcular la temperatura efectiva en los distintos planetas hay que hacer el cálculo del balance radiativo terrestre pero generalizado para los planetas. Se supone que cada planeta ha alcanzado el equilibrio interceptando del Sol la misma energía que irradia por su temperatura.
 siendo r el radio del planeta.
siendo r el radio del planeta.
 siendo a el albedo
siendo a el albedo
La razón del 4 radica en que sólo la sección del planeta intersecciona la energía solar mientras que toda la superficie del planeta la irradia.
Como la energía absorbida e irradiada son iguales por el equilibrio térmico resulta:
La evaluación de la fórmula da las distintas temperaturas efectivas de los planetas. Estas temperaturas no deben confundirse con temperaturas superficiales, pues la atmósfera y las nubes reflejan parte de la radiación solar de onda corta mientras las ondas largas emitidas por la radiación térmica del planeta son absorbidas en parte por los gases de efecto invernadero aumentando significativamente la temperatura superficial especialmente en el caso de Venus mientras que si la atmósfera es delgada como en el caso de Marte no debe haber mucha diferencia.
| Planeta | K (W/m²) | K/K0 | Albedo | Te (K) |
|---|---|---|---|---|
| Mercurio | 9040 | 6,7 | 0,058 | 442 |
| Venus | 2610 | 1,9 | 0,71 | 244 |
| Tierra | 1360 | 1 | 0,33 | 253 |
| Marte | 590 | 0,4 | 0,17 | 216 |
| Júpiter | 50 | 0,04 | 0,52 | 87 |
| Saturno | 15 | 0,01 | 0,47 | 63 |
| Urano | 3,7 | 0,003 | 0,51 | 33 |
| Neptuno | 1,5 | 0,001 | 0,41 | 32 |
Radiación Solar
| Índice Conceptos de Visión Visión del Color Referencia Wyszecki & Stiles Cap. 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Atrás |
La Constante SolarLa cantidad de energía solar, que llega a la parte superior de la atmósfera de la Tierra por metro cuadrado de superficie perpendicular, se llama a menudo constante solar. El valor nominal de la constante solar esLa medida real de la radiación solor varia con la altitud y la orientación con el Sol. |



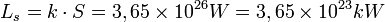
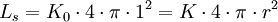



![T_e=\sqrt [4] {\frac {K \cdot (1-a)}{4\cdot \sigma}} \,](https://upload.wikimedia.org/math/3/0/9/3091d9e437f725a77633dd796554b17c.png)
No hay comentarios:
Publicar un comentario