ARITMÉTICA

ARITMÉTICA ELEMENTAL

y=x³, para valores enteros que satisfacen 1≤x≤25 en un sistema de coordenadas cartesianas.

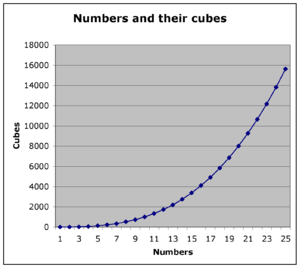
En aritmética y álgebra, el cubo de un número n es la tercera potencia —el resultado de multiplicar por sí mismo tres veces:¹​

${\displaystyle n^{3}=n\cdot n\cdot n}$

En geometría, es la ecuación para obtener el volumen de un cubo de lado a:

${\displaystyle V=a\cdot a\cdot a=a^{3}\,}$

Propiedades[editar]

A diferencia del cuadrado de un número, no existe el número cubo más pequeño, debido a que se incluyen los números negativos. Por ejemplo, (−4) × (−4) × (−4) = −64. Para cualquier n, (−n)³ = −(n³).

A diferencia de los cuadrados perfectos, los cubos perfectos no tienen una pequeña cantidad de posibilidades excepto para los dos últimos dígitos. Excepto para los cubos divisibles por 5, donde únicamente 25 y 75 pueden ser los dos últimos dígitos, cualquier par de dígitos con los últimos dígitos impares puede ser un cubo perfecto. Con los cubos pares, hay una considerable restricción, solo para 00, i2, p4, i6 y p8 puede que los dos últimos dígitos de un cubo perfecto (donde i significa cualquier dígito impar y p para dígitos pares). Algunos números cúbicos son también números cuadrados, por ejemplo 64 es un cuadrado (8 × 8) y al mismo tiempo un cubo (4 × 4 × 4); esto ocurre si y solo si es una sexta potencia perfecta. Cabe esa posibilidad si el expontente k es múltiplo de 6, para la duodécima, décima octava potencia, etc.

Un Cubo de Rubik de 3x3x3 compuesto de 27 (26) pequeños cubos.

Sin embargo, es fácil ver que la mayoría de los números no son cubos perfectos a causa de que todos los cubos perfectos deben tener una raíz digital 1, 8 o 9. De esta forma, la raíz digital de cualquier número queda determinada por el resto del número cuando es dividido entre 3:

• Si el número es divisible entre 3, su cubo tiene como raíz digital al 9;
• Si tiene como resto 1 cuando es dividido entre 3, su cubo tiene la raíz digital igual a 1;
• Si tiene como resto 2 cuando es dividido entre 3, su cubo tiene como raíz digital 8.

Cada entero positivo puede ser escrito como la suma de nueve cubos o incluso menos, véase problema de Waring. Este límite superior de nueve cubos no puede ser reducido ya que, por ejemplo, 23 no puede ser escrito como la suma de menos de nueve cubos:

23 = 2³ + 2³ + 1³ + 1³ + 1³ + 1³ + 1³ + 1³ + 1³

El número m es un cubo perfecto si y solo si pueden ordenarse m puntos en un cubo, por ejemplo 3 × 3 × 3 = 27. La suma de los primeros n cubos perfectos es un n-ésimo número triangular al cuadrado:

${\displaystyle 1^{3}+2^{3}+...+n^{3}=\left({\frac {n(n+1)}{2}}\right)^{2}}$

Por ejemplo, la suma de los primeros cinco números cubos perfectos, 1³ + 2³ + 3³ + 4³ + 5³, es igual a la suma de los cinco primeros números triangulares 15² que es 225.

Otras características[editar]

• (mn)³ = m³n³
• (m+n)³ = m³ +3m²n +3mn² +n³
• Si m > n, entonces m³ > n³ ( función creciente)
• Sea H = {n³/ n es n. natural}, H tiene mínimo
• Si n > 1, entones n³ > n² > n
• m³ +n³ = (m²-mn+ n²)(m+n)
• Hay una identidad análoga para la diferencia de cubos, basta en la anterior, cambiar n por -n
• Si al producto de tres términos consecutivos de una progresión aritmética, de término inicial m y diferencia r, se le agrega kr², donde k término intermedio, se obtiene un cubo perfecto,K, m y r son enteros positivos.
• l producto de tres términos consecutivos de una progresión geométrica es un cubo perfecto.
• La media geométrica de tres números siempre existe sin importar el signo de los números.²​

En fórmulas geométricas[editar]

• En el volumen de la esfera aparece el cubo del radio o el cubo del díámetro.
• En el volumen del cubo, de modo emblemático.
• En el volumen del tetraedro regular, figura el cubo de la arista.
• El cubo del seno de un arco conlleva el seno del arco y el seno del arco triple.³​

Relación con otras funciones[editar]

La función inversa a encontrar un número cuyo cubo es n se denomina extracción de la raíz cúbica de n. La operación es similar a encontrar la arista de un cubo de volumen conocido. También se dice que n elevado un tercio.

Suma interesante[editar]

${\displaystyle 20^{3}=17^{3}+14^{3}+7^{3}}$.

En vez de hacer tres depósitos cúbicos de aristas 17, 14 y 7 m respectivamente, si se reemplaza por un depósito cúbico de arista 20 m, se ahorra en costo de material y se usa en menos cantidad. Pero la misma capacidad.

Casos vinculados[editar]

• Un clásico problema de cubos, demoró en hallar su solución, por la irracionalidad de un factor numérico. Se trataba de calcular la arista de un cubo que tenga el doble de volumen del cubo del oráculo de Delfos.⁴​
• Un dato al cubo aparece en la fórmula del volumen de un cubo, de una esfera, tetraedro regular, de un octaedro, dodecaedro, icosaedro regulares, en la suma de los cuadrados de los primeros n naturales, que conlleva tres sumandos o términos: ${\displaystyle S=n^{3}/3+n^{2}/2+n/6}$⁵​

En matemáticas, concretamente en aritmética, se dice que un número entero b es divisible por otro entero a (no nulo) si existe un entero c tal que: ${\displaystyle b=a\cdot c}$. Esto es equivalente a decir que el resto de la división euclídea es cero o simbólicamente ${\displaystyle b-a\cdot c=0}$.

Se suele expresar de la forma ${\displaystyle a\mid b}$, que se lee: «a divide a b», o «a es un divisor de b» o también «b es múltiplo de a».¹​ Por ejemplo, 6 es divisible por 3, ya que 6 = 3·2; pero 6 no es divisible por 4, pues no existe un entero c tal que 6 = 4·c, es decir que el resto de la división euclídea (entera) de 6 entre 4 no es cero.

Cualquier número entero es divisible por 1 y por sí mismo. Los números mayores que 1 que no admiten más que estos dos divisores se llaman números primos. Los que admiten más de dos divisores se llaman números compuestos.

Definición[editar]

El número entero ${\displaystyle a}$ es divisible por el número entero ${\displaystyle b\neq 0}$ (o lo que es lo mismo, b divide a a) si hay un número ${\displaystyle q}$ entero, tal que ${\displaystyle a=b\cdot q}$.

Este hecho se denomina divisibilidad del número entero ${\displaystyle a}$ por el número entero ${\displaystyle b}$ y se denota por ${\displaystyle b|a}$; que no es otra cosa que una afirmación entre los números enteros, que, en un contexto concreto, puede ser cierta o no.²​ Por ejemplo ${\displaystyle 3|12}$ es cierta; sin embargo, ${\displaystyle 3|17}$ no es cierta. Si ${\displaystyle b}$ no es divisor de ${\displaystyle a}$ escribimos ${\displaystyle b\nmid a}$. Notemos que ${\displaystyle 0\nmid a}$ para todo ${\displaystyle a}$ distinto de cero, pues ${\displaystyle a\neq 0=k\cdot 0}$ para todo ${\displaystyle k}$ entero.

Factor o divisor propio[editar]

Se denomina factor o divisor propio de un número entero n, a otro número también entero que es divisor de n, pero diferente de n. Los divisores 1 y n son denominados impropios.

Por ejemplo, los divisores propios de 28 son 1, 2, 4, 7 y 14. Cuando se toman en cuenta enteros negativos, un divisor propio es aquel cuyo valor absoluto es menor al número dado. En este caso, los divisores propios serían -14, -7, -4, -2, -1, 1, 2, 4, 7, 14.

Casos especiales: 1 y -1 son factores triviales de todos los enteros, y cada entero es divisor de 0. Los números divisibles por 2 son llamados pares y los que no lo son se llaman impares.

Si d es un divisor de a y no admite más divisor propio que la unidad, de llama divisor primo de a. De hecho es un número primo. El 1 es el único entero que tiene un solo divisor positivo.

Propiedades[editar]

Sean ${\displaystyle a,b,c\in \mathbb {Z} }$, es decir ${\displaystyle \ a}$, ${\displaystyle \ b}$ y ${\displaystyle \ c}$ son números enteros. Tenemos las propiedades básicas:

• ${\displaystyle a\mid a}$ (Propiedad reflexiva).
• si ${\displaystyle a\mid b}$ y ${\displaystyle b\mid a}$ entonces ${\displaystyle |a|=|b|}$ . Son iguales o bien uno es el opuesto del otro.
• Cuando ${\displaystyle a\mid b}$ y ${\displaystyle b\mid c}$, entonces ${\displaystyle a\mid c}$ (Propiedad transitiva).
• Si ${\displaystyle a\mid b}$ y ${\displaystyle b\neq 0}$, entonces ${\displaystyle |a|\leq |b|}$.
• ${\displaystyle a\mid b}$ y ${\displaystyle a\mid c}$, implica ${\displaystyle a\mid \beta b+\gamma c\ \ \forall \ \beta ,\gamma \in \mathbb {Z} }$.
• Si ${\displaystyle a\mid b}$ y ${\displaystyle a\mid b\pm \ c}$, entonces ${\displaystyle a\mid c}$
• De ${\displaystyle a\mid b}$ y ${\displaystyle a\neq 0}$, se deduce ${\displaystyle {\frac {b}{a}}\mid b}$.
• Para ${\displaystyle c\neq 0}$, ${\displaystyle a\mid b}$ si y sólo si ${\displaystyle ac\mid bc}$
• Si ${\displaystyle a\mid bc}$ y ${\displaystyle \ \operatorname {mcd} (a,b)=1}$, entonces ${\displaystyle a\mid c}$.
• Cuando ${\displaystyle \ \operatorname {mcd} (a,b)=1}$ y ${\displaystyle \ c}$ cumple que ${\displaystyle a\mid c}$ y ${\displaystyle b\mid c}$, entonces ${\displaystyle ab\mid c}$.
• ${\displaystyle n\mid 0}$ y ${\displaystyle 1\mid n}$ para todo ${\displaystyle \ n}$ entero ya que ${\displaystyle 0=0\cdot n}$ y ${\displaystyle n=n\cdot 1}$.
• ${\displaystyle 1\mid \operatorname {mcd} (a,b)\mid a\mid \operatorname {mcm} (a,b)\mid 0}$
• abcd es divisible por n-1 si, sólo si a+b+c+d es múltiplo de (n-1), siempre que abcd esté escrito en la base n, (n≥ 3 ) ³​.
• Si mcd(a,b) = 1 no cabe a^k = b^h para cualesquiera h, k números enteros positivos; potencias de coprimos no son iguales en ningún caso. ⁴​

Número de divisores[editar]

Si la factorización en números primos de n viene dada por

${\displaystyle n=p_{1}^{\nu _{1}}\,p_{2}^{\nu _{2}}\cdots p_{k}^{\nu _{k}}}$

entonces el número de divisores positivos de n es

${\displaystyle d(n)=(\nu _{1}+1)(\nu _{2}+1)\cdots (\nu _{k}+1),}$

y cada uno de los divisores tiene la forma

${\displaystyle p_{1}^{\mu _{1}}\,p_{2}^{\mu _{2}}\cdots p_{k}^{\mu _{k}}}$

donde ${\displaystyle 0\leq \mu _{i}\leq \nu _{i}}$ para cada ${\displaystyle 1\leq i\leq k.}$ ⁵​

Criterios de divisibilidad[editar]

Los siguientes criterios nos permiten averiguar si un número es divisible por otro de una forma sencilla, sin necesidad de realizar la división.

Número	Criterio	Ejemplo
2	El número termina en una cifra par (0, 2, 4, 6, 8).	378: porque la última cifra (8) es par.
3	La suma de sus cifras es un múltiplo de 3.	480: porque 4+ 8+ 0 = 12 es múltiplo de 3.
4	El número formado por las dos últimas cifras es un múltiplo de 4 o cuando termina en doble cero. O bien, si el resultado de sumar el doble del penúltimo dígito y el último da un número divisible entre 4.	7324: porque 24 es múltiplo de 4. 8200: porque termina en 00. 5232: porque 3*2+2=8 y 8 es múltiplo de 4.
5	La última cifra es 0 o 5.	485: porque termina en 5.
6	El número es divisible entre 2 y entre 3 a la vez.	18: es múltiplo de 2 y de 3 a la vez.
7	Un número es divisible entre 7 cuando, al separar la última cifra de la derecha, multiplicarla por 2 y restarla de las cifras restantes la diferencia es igual a 0 o es un múltiplo de 7.	34349: separamos el 9,y lo doblamos (18), entonces 3434-18=3416. Repetimos el proceso separando el 6 (341'6) y doblándolo (12), entonces 341-12=329, y de nuevo, 32'9, 9*2=18, entonces 32-18=14; por lo tanto, 34349 es divisible entre 7 porque 14 es múltiplo de 7.
8	Un número es divisible por 8 si el número formado por las tres últimas cifras es un múltiplo de 8 o termina en tres ceros.	27280: porque 280 es múltiplo de 8.
9	Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9.	3744: porque 3+7+4+4= 18 es múltiplo de 9.
10	Un número es divisible por 10 si su última cifra es 0.	470: termina en cifra 0.
11	Sumando las cifras (del número) en posición impar por un lado y las de posición par por otro. Luego se resta el resultado de ambas sumas obtenidas. Si el resultado es cero (0) o un múltiplo de 11, el número es divisible por éste. Si el número tiene sólo dos cifras y estas son iguales será múltiplo de 11.	42702: 4+7+2=13 · 2+0=2 · 13-2=11 → 42702 es múltiplo de 11 66: porque las dos cifras son iguales. Entonces 66 es Múltiplo de 11
12	Un número es divisible por 12 cuando al hacer la división, siendo el cociente 3 o 4, su resto da como resultado 0.	420: es múltiplo de 3 ya que 4+2+0=6 y de 4 puesto que 20 también lo es. Por tanto es múltiplo de 12.
13	Un número es divisible entre 13 cuando, al separar la última cifra de la derecha, multiplicarla por 9 y restarla de las cifras restantes la diferencia es igual a 0 o es un múltiplo de 13	3822: separamos el último dos (382'2) y lo multiplicamos por 9, 2*9=18, entonces 382-18=364. Repetimos el proceso separando el 4 (36'4) y multiplicándolo por 9, 4*9=36, entonces 36-36=0; por lo tanto, 3822 es divisible entre 13
14	Un número es divisible entre 14 cuando es par y divisible entre 7	546: separamos el último seis (54'6) y lo doblamos, 6*2=12, entonces 54-12=42. 42 es múltiplo de 7 y 546 es par; por lo tanto, 546 es divisible entre 14
15	Un número es divisible entre 15 cuando es divisible entre 3 y 5	225: termina en 5 y la suma de sus cifras es múltiplo de 3; por lo tanto, 225 es divisible entre 15
17	Un número es divisible entre 17 cuando, al separar la última cifra de la derecha, multiplicarla por 5 y restarla de las cifras restantes la diferencia es igual a 0 o es un múltiplo de 17	2142: porque 214'2, 2*5=10, entonces 214-10=204, de nuevo, 20'4, 4*5=20, entonces 20-20=0; por lo tanto, 2142 es divisible entre 17.
18	Un número es divisible por 18 si es par y divisible por 9 (Si es par y además la suma de sus cifras es múltiplo de 9)	9702: Es par y la suma de sus cifras: 9+7+0+2=18 que también es divisible entre 9. Y efectivamente, si hacemos la división entre 18, obtendremos que el resto es 0 y el cociente 539.
19	Un número es divisible por 19 si al separar la cifra de las unidades, multiplicarla por 2 y sumar a las cifras restantes el resultado es múltiplo de 19.	3401: separamos el 1,lo doblamos (2) y sumamos 340+2= 342, ahora separamos el 2, lo doblamos (4) y sumamos 34+4=38 que es múltiplo de 19, luego 3401 también lo es.
20	Un número es divisible entre 20 si sus dos últimas cifras son ceros o múltiplos de 20	57860: Sus 2 últimas cifras son 60 (Que es divisible entre 20), por lo tanto 57860 es divisible entre 20.
25	Un número es divisible entre 25 si sus dos últimas cifras son 00, o en múltiplo de 25 (25,50,75,...)	650: Es múltiplo de 25 por lo cual es divisible. 400: Termina en 00, por lo tanto también será divisible entre 25.
29	Un número es divisible por 29 si al separar la cifra de las unidades, multiplicarla por 3 y sumar a las cifras restantes el resultado es múltiplo de 29.	2262: separamos el último 2, lo triplicamos (6) y sumamos, 226+6= 232, ahora separamos el último 2, lo triplicamos (6) y sumamos 23+6=29 que es múltiplo de 29, luego 2262 también lo es.
31	Un número es divisible por 31 si al separar la cifra de las unidades, multiplicarla por 3 y restar a las cifras restantes el resultado es múltiplo de 31.	8618: separamos el 8, lo triplicamos (24) y restamos 861-24=837, ahora separamos el 7, lo triplicamos (21) y restamos, 83-21=62 que es múltiplo de 31, luego 8618 también lo es.
100	Un número será divisible por 100 si dicho número termina en 00.	1000: Este número será divisible por cien ya que sus dos últimas cifras son 00, independientemente de las demás.
125	Un número será divisible por 125 si sus tres últimas cifras son 00 o múltiplo de 125.	3000: Sería divisible por 125 ya que sus tres últimas cifras son 00. 4250: Este número también sería divisible por 125 ya que sus tres últimas cifras son múltiplo de 125.

Nota 1: Existen muchas versiones de los criterios de divisibilidad. Así por ejemplo, para el 13 resulta equivalente el criterio: al separar la última cifra de la derecha, multiplicarla por 4 y sumarla a las cifras restantes la suma es igual a 0 o es un múltiplo de 13.

Nota 2: Resulta curioso que el criterio de divisibilidad por 7 sirva también como criterio de divisibilidad por 3, aunque evidentemente el criterio tradicional resulta más sencillo y éste no se utiliza: al separar la última cifra de la derecha, multiplicarla por 2 y restarla de las cifras restantes la diferencia es igual a 0 o es un múltiplo de 3.

Nota 3: Aunque existen criterios similares para cualquier número primo, con frecuencia resulta más sencillo dividir que aplicar un criterio complicado (como el del 13). Sin embargo existe un criterio general que funciona siempre y que en muchos casos es suficientemente práctico: restar el número primo (o múltiplos de éste) a las cifras de la izquierda sucesivamente hasta obtener cero o ese número primo. Así el ejemplo del 13 se podría comprobar con el proceso siguiente (usamos el 39 =3*13 para abreviar pasos): 3822 (restamos 13 dos veces a la izquierda) → 2522 → 1222 (restamos 39 tres veces de las tres cifras de la izquierda) → 832 → 442 → 52 y al restar de nuevo 39 obtenemos 52-39 =13

Nota 4: El método no tiene que ceñirse sólo al proceso de quitar las unidades. Pueden quitarse unidades y decenas. Así por ejemplo: 201 es múltiplo de 67. Un criterio para el 67 sería: quitamos el número formado por las decenas y unidades y se lo restamos 2 veces a las cifras que quedan, si el resultado es múltiplo de 67, el número anterior también lo será. Ejemplo: 66129, hacemos 661-2·29=603, Ahora 6 -2·3=0, luego 66129 es múltiplo de 67.

Una prueba de esto es la siguiente: (N-d)/100-2d = (N-d-200d)/100 = (N - 201d)/100= k. Si k es múltiplo de 67, N también lo será puesto que N = 100k+201d.

Nota 5: Para saber si un número de 3 cifras es múltiplo de 8. Hay que tener en cuenta lo siguiente: Si la cifra de las centenas es par y las otras 2 es un múltiplo de 8 (288→ 2 es cifra par, y 88 múltiplo de 8) o si la cifra de las centenas es impar y las dos últimas son el resultado de la diferencia o suma de un múltiplo de 8 con 4 (168→ 1 es cifra impar y 68+4=72; 72 es múltiplo de 8.

Nota 6: Todo número de tres cifras, en el cual las tres cifras son iguales, es múltiplo de 37; de hecho es la multiplicación de 37 por la suma de sus cifras. Ejemplo: 333 es múltiplo de 37, porque 333=37*9 (3+3+3=9).

Observación[editar]

Todos los criterios señalados funcionan si el número está escrito en el sistema de numeración decimal. En otra base no siempre ocurre así. Pues 102₇, escrito en base 7, termina en cifra par, pero no es divisible por 2. En este caso se suman las cifras 1+2=3; 3=1 (Mód 2), luego 102₇ es impar (en decimal es 7²+2=51).

división euclidiana (o euclídea), también llamada algoritmo de la división, es un teorema que asegura que «el proceso habitual de división entre números enteros» puede llevarse a cabo y que se obtiene un cociente y un residuo únicos.

Un «algoritmo de división entera» es cualquier método efectivo que produce un cociente y un residuo. Existen numerosos métodos para efectuar estos cálculos, como por ejemplo la división larga, la factorización de enteroso la aritmética modular. El algoritmo de la división euclídea (para números enteros) se encuentra a la base de numerosos resultados de la aritmética (como por ejemplo el algoritmo de Euclides para calcular el máximo común divisor de dos enteros) y la teoría de números; en álgebra abstracta, está relacionado con el dominio euclídeo.

División euclídea de números naturales[editar]

Igual que el Teorema de Bolzano pero con números imaginarios y en divisiones que pueden ser en fracciones homogéneas o impropias.

Dados dos números naturales, el dividendo, m, y el divisor, d, que debe ser mayor que cero, llamamos cociente, q, al mayor de los números que multiplicado por el divisor es menor o igual que el dividendo.

${\displaystyle q\;=\;\max \ \{\ x\in N\;|\;xd\leq m\ \}}$

Llamamos resto, r, a la diferencia entre el dividendo y el producto del cociente y el divisor.

${\displaystyle r\;=\;m-qd}$

El resto verifica la inecuación ${\displaystyle 0\leq r$ .

De la ecuación anterior, se deduce inmediatamente la siguiente:

${\displaystyle m\;=\;qd+r}$

Ejemplos[editar]

${\displaystyle 320\,}$		${\displaystyle 21\,}$
${\displaystyle 110\,}$		${\displaystyle 15\,}$
${\displaystyle 5\,}$

lo que significa que ${\displaystyle 320=(21\times 15)+5}$, con ${\displaystyle 0\leq 5<\mid 21\mid }$.

Teorema: Algoritmo de la división[editar]

División euclídea con números naturales[editar]

Dados dos números naturales a y b, con b distinto de 0, la división euclídea asocia un cociente q y un resto r, ambos números naturales, que verifican:

• ${\displaystyle a=b\ q+r\,}$
• ${\displaystyle r$

La pareja (q, r) es única.

De manera formal:

${\displaystyle \forall (a,b)\in \mathbb {N} \times \mathbb {N} ^{*},\exists !(q,r)\in \mathbb {N} ^{2}/a=b\ q+r\quad {\text{con}}\quad r$

mostrarTeorema de la división euclídea para los números naturales

División euclídea con números enteros[editar]

Dados dos números enteros a y b, con b no nulo, la división euclídea asocia un cociente q y un resto r, ambos números enteros, que verifican:

• ${\displaystyle a=b\cdot q+r\,}$
• ${\displaystyle 0\leq r<|b|}$¹​

• A q se denomina cociente y a r, resto de la división que siempre es un entero no negativo.²​³​

De manera formal:

${\displaystyle \forall (a,b)\in \mathbb {Z} \times \mathbb {Z} ^{*},\exists q,r\in \mathbb {Z} |a=b\cdot q+r\quad {\text{con}}\quad 0\leq r<|b|}$

mostrarTeorema de la división euclídea para los números enteros

Propiedades[editar]

Por el algoritmo de la división se deduce que ${\displaystyle \mathbb {Z} }$ es un dominio euclídeo tomando como norma el valor absoluto. Una consecuencia inmediata del algoritmo de la división es que puede usarse el algoritmo de Euclides para calcular el máximo común divisor de dos números enteros.

Un concepto que generaliza el algoritmo de la división es el de norma euclídea. De este modo cualquier dominio euclídeo cumple con un principio similar al algoritmo de la división, como es el caso, por ejemplo, de un anillo de polinomios ${\displaystyle \mathbb {K} [x]}$ en que ${\displaystyle \mathbb {K} }$ es un cuerpo.

División de polinomios[editar]

Artículo principal: División polinomial

La división euclidiana se generaliza a todos los anillos graduados, es decir en los anillos donde existe una función llamada grado que verifique: d ^o(P·Q) = d ^o(P) + d ^o(Q).

Los ejemplos más usuales lo constituyen los anillos de polinomios K[X], donde K es un cuerpo, como R o C, y donde d ^o(Xⁿ) = n y d ^o(0) = - ∞. En este contexto, se remplaza la condición 0≤ r < b que a priori no tiene sentido porque el anillo ya no es totalmente ordenado, por d ^o (R) < d ^o(B), y claro, se mantiene A = B·Q + R (para los polinomios, la costumbre es utilizar las mayúsculas).

Si los polinomios tienen por coeficientes elementos de un cuerpo K, es posible definir una división euclídea sobre los polinomios (llamada división) según el orden decreciente de las potencias.

A dos polinomios A y B, la división euclídea asocia un único cociente Q y un único resto R, ambos polinomios, tales que:

• ${\displaystyle A=B\cdot Q+R\,}$
• ${\displaystyle \operatorname {grad} (R)<\operatorname {grad} (B)}$

Formalmente:

${\displaystyle \forall (A,B)\in \mathbb {K} [X]\times \mathbb {K} [X]^{*},\quad \exists !Q,R\in \mathbb {K} [X],A=B\cdot Q+R\quad \mathrm {con} \quad \operatorname {grad} (R)<\operatorname {grad} (B)}$

La unicidad está garantizada, pero es necesario que K sea un cuerpo para que la existencia lo sea también.