GEOMETRÍA

FIGURAS GEOMÉTRICAS - CURVAS

Esquema de una arco de circunferencia.
c: cuerda; f: flecha; s: arco, d: apotema.

En geometría, la flecha o sagita de un arco circular es la distancia desde el centro del arco al centro de la cuerda.¹​ Este concepto se emplea a menudo en arquitectura para obtener el arco necesario para cubrir un vano y en óptica en donde se emplea para hallar la profundidad de un espejo esférico o una lente.

Expresiones[editar]

En las siguientes expresiones, ${\displaystyle f}$ se refiere a la flecha, ${\displaystyle R}$ al radio de la circunferencia, ${\displaystyle c}$ a la cuerda del arco y ${\displaystyle d}$ a la distancia desde el centro de la circunferencia hasta la cuerda.

La flecha se define como:

${\displaystyle f=R-d}$

Aplicando el Teorema de Pitágoras, la flecha se puede calcular como:

${\displaystyle f=R-{\sqrt {R^{2}-\left({\frac {c}{2}}\right)^{2}}}}$

La flecha también se puede calcular empleando la función verseno. Sea ${\displaystyle \alpha }$ el ángulo que define el arco,

${\displaystyle f=R\cdot \operatorname {versin} {\frac {\alpha }{2}}=R\left(1-\cos {\frac {\alpha }{2}}\right)}$

O de forma alternativa:

${\displaystyle f={\frac {c}{2}}\cdot \tan {\frac {\alpha }{4}}}$

Cuando la flecha es pequeña en comparación con el radio se puede aproximar de la siguiente forma:²​

${\displaystyle f\approx {\frac {\left(c/2\right)^{2}}{2R}}={\frac {c^{2}}{8R}}}$

Curva logística, normalizada: ${\displaystyle P(t)={\frac {1}{1+e^{-t}}}}$

La función logística, curva logística o curva en forma de S es una función matemática que aparece en diversos modelos de crecimiento de poblaciones, propagación de enfermedades epidémicas y difusión en redes sociales. Dicha función constituye un refinamiento del modelo exponencial para el crecimiento de una magnitud. Modela la función sigmoidea de crecimiento de un conjunto P.

El estudio inicial de crecimiento es aproximadamente exponencial; al cabo de un tiempo, aparece la competencia entre algunos miembros de P por algún recurso crítico K ("cuello de botella") y la tasa de crecimiento disminuye; finalmente, en la madurez, el crecimiento se detiene.

La función logística simple se define mediante la expresión matemática:

(1)${\displaystyle P(t)={\frac {1}{1+e^{-t}}}}$

donde la variable P puede ser considerada o denotada como población, donde e es la constante de Euler y la variable t puede ser considerada el tiempo.¹​ Para valores de t en el rango de los números reales desde −∞ a +∞, la curva S se puede obtener. En la práctica, dada la naturaleza de la función exponencial, e^−t, es suficiente con computar t para un pequeño rango de números reales como pueden ser [−6, +6].

En su forma más general, la función logística se define por la fórmula matemática:

(2)${\displaystyle P(t;a,m,n,\tau )=a{\frac {1+me^{-t/\tau }}{1+ne^{-t/\tau }}}\!}$

para parámetros reales a, m, n, y ${\displaystyle \tau }$. Estas funciones tienen un campo de aplicación muy amplio, desde la biología a la economía.

Función logística

Comenzaremos con un breve repaso  de la función exponencial ya que la función a estudiar está relacionada con ella.

                                                               

En el estudio de la función exponencial hay que tener en cuenta que la base a es siempre positiva y que hay dos tipos claramente diferenciados dependiendo de si   a > 1   ó      0 < a < 1.

1. A la vista de la escena anterior (puedes mover el punto P a lo largo del eje de abscisas para ver cómo varía la ordenada) repasa las propiedades y la representación gráfica de las funciones exponenciales
2. Resuelve en tu libreta:

En el contrato de trabajo de un empleado figura que su sueldo subirá un 4% anual. Si empieza ganando 5 Millones, ¿cuánto ganará dentro de 3 años?, ¿cuánto tardará en duplicar su sueldo?

      3. Comprueba los resultados obtenidos utilizando la escena superior. 

---

La función exponencial es un modelo válido para crecimientos o decrecimientos continuos en los que las condiciones son  siempre  igualmente favorables: aumento del capital ingresado en un banco, desintegración de sustancias radioactivas...Las poblaciones de seres vivos comienzan creciendo según una curva exponencial  pero si no hay catástrofes, llegan a invadir su espacio vital y, debido a la limitación de alimentos, etc., su crecimiento se amortigua, no sobrepasando su población límite. Este tipo de aumento, amortiguado por un nivel de saturación se llama crecimiento logístico.

La función logística describe mucho mejor que la exponencial lo que realmente ocurre con las poblaciones de seres vivos.

En general, la función logística asociada a una exponencial es:

        FUNCIÓN EXPONENCIAL            donde C  es la población inicial,   x   el tiempo

        FUNCION LOGÍSTICA         donde L es la población límite,  K = ( L / C ) - 1

UN CASO REAL:

En una isla dejamos escapar 100 conejos, especie desconocida hasta entonces en esos parajes. Supongamos que las condiciones para que se reproduzcan son óptimas, por lo que se incrementan en un 10% mensual (hasta aquí sería un modelo exponencial típico).

Supongamos ahora que la isla tuviera un tamaño y unas condiciones tales que, a lo sumo pudieran vivir 1000 conejos . Este número sería nuestra población límite. En este caso la función que describe el crecimiento es la función logística asociada. Observa en la siguiente escena sus características.  L = 1000  y   K = 9.

En la siguiente tabla se observa el número de conejos que habría en la isla según cada modelo.

MES	LOGÍSTICA	EXPONENCIAL	DIFERENCIA
0	10	10	0
1	10,89108911	11	0,108910891
2	11,85112635	12,1	0,248873653
3	12,88355435	13,31	0,426445649
4	13,99164763	14,641	0,649352367
5	15,178441	16,1051	0,926659001
6	16,44665058	17,71561	1,268959417
7	17,79858848	19,487171	1,688582524
8	19,23607239	21,4358881	2,199815713
9	20,76033237	23,57947691	2,819144541
10	22,37191717	25,9374246	3,565507431
11	24,07060334	28,53116706	4,460563718
12	25,85531075	31,38428377	5,528973019
13	27,72402845	34,52271214	6,798683692
14	29,67375526	37,97498336	8,301228096
15	31,70045912	41,77248169	10,07202257
16	33,79905934	45,94972986	12,15067053
17	35,963435	50,54470285	14,58126785
18	38,18646215	55,59917313	17,41271099
19	40,46008101	61,15909045	20,69900944
20	42,77539323	67,27499949	24,49960626
21	45,12278758	74,00249944	28,87971187
22	47,49209081	81,40274939	33,91065858
23	49,87273923	89,54302433	39,6702851
24	52,25396479	98,49732676	46,24336197

Fíjate cómo durante los  primeros meses los números son casi idénticos: aún estaba lejos el nivel de saturación. Sin embargo, al aumentar el tiempo la diferencia es enorme y después los resultados obtenidos para cada modelo no tienen nada que ver.

https://es.wikipedia.org/wiki/Funci%C3%B3n_log%C3%ADstica

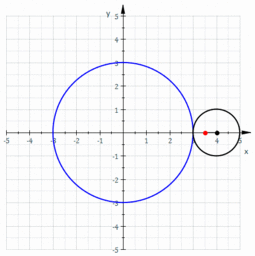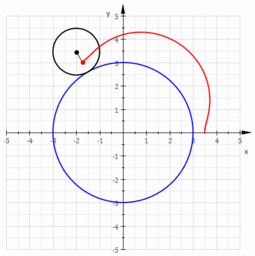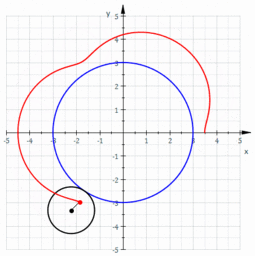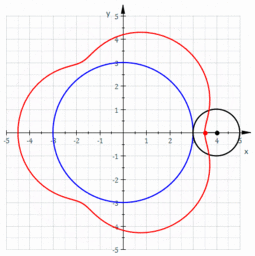
La generatriz¹​ es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva que conforma un círculo.²​

Si la generatriz es una línea recta que gira respecto de otra recta directriz, llamada eje de rotación, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es una curva, genera esferas, elipsoides, etc. Si se desplaza sobre una o más directrices, genera una superficie reglada.

La generatriz puede ser una línea curva, por ejemplo, una circunferencia que rueda sobre otra circunferencia directriz, tangencialmente. Un punto vinculado a ella describe una trayectoria curva que se denomina ruleta cicloidal.

En la figura, la circunferencia de color azul es la directriz, y la circunferencia de color negro es la generatriz. Un punto vinculado a ella describe una forma llamada epitrocoide: la curva de color rojo.

Curvas conformadas por circunferencias generatrices[editar]

Artículo principal: Ruleta (curva)

• Cicloide, la curva plana generada por un punto de una circunferencia generatriz al rodar sobre una línea recta, sin deslizarse.
• Epicicloide, la curva que describe un punto vinculado a una circunferencia generatriz que rueda –sin deslizamiento– sobre una circunferencia directriz, tangencialmente.
• Hipocicloide, la curva que describe la trayectoria un punto situado sobre una circunferencia generatriz que rueda por el interior de otra circunferencia directriz, sin deslizamiento.
• Trocoide, la curva plana que describe un punto, vinculado a una circunferencia generatriz, que rueda sobre una línea recta directriz, tangencialmente, sin deslizamiento.
• Epitrocoide, la curva que describe un punto vinculado a una circunferencia generatriz que rueda –sin deslizamiento– sobre una circunferencia directriz, tangencialmente.
• Hipotrocoide, la curva plana que describe un punto vinculado a una circunferencia generatriz que rueda dentro de una circunferencia directriz, tangencialmente, sin deslizamiento.

Generatriz del cilindro[editar]

El cilindro es un cuerpo de revolución engendrado por un rectángulo al girar en torno a uno de sus lados. La altura del cilindro coincide con la longitud del lado sobre el que gira el cilindro. El otro lado opuesto al contenido en el eje de giro, se llama línea generatriz y su longitud coincide con la de la apotema del cuadrado.

También podría generarse un cilindro a partir de un círculo generatriz al desplazarse éste a lo largo de una recta ortogonal al plano del círculo. Si el círculo generatriz en lugar de desplazarse por una línea recta ortogonal se desplazase en una trayectoria circular cerrada en un plano ortogonal (al plano del círculo) se obtendría un toro.

Generatriz del cono[editar]

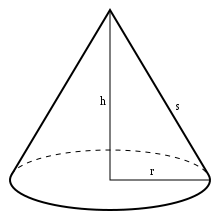
El cono es un cuerpo de revolución engendrado por un triángulo rectángulo al girar en torno a uno de sus catetos, que será la altura del cono y la hipotenusa será la generatriz. Por el teorema de Pitágoras la longitud de la generatriz s del cono será igual a:

${\displaystyle s^{2}=h^{2}+r^{2}}$

donde h es la altura del cono y r el radio de su base.

Generatriz del tronco de cono[editar]

El tronco de cono es un cuerpo de revolución se ha engendrado por un trapecio rectángulo al girar en torno al lado perpendicular a las bases, que será la altura del cono y el otro lado será la generatriz.

Obtenemos la generatriz del tronco de cono aplicando el teorema de Pitágoras en el triángulo sombreado:

${\displaystyle l^{2}=h^{2}+(R-r)^{2}}$