GEOMETRÍA

FIGURAS GEOMÉTRICAS - CURVAS

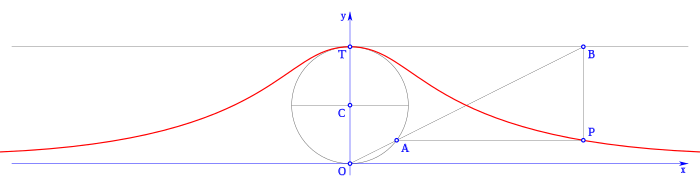
Generación de la curva.

En matemáticas, particularmente en el cálculo y en geometría analítica, la Curva de Agnesi(pronunciado 'añesi'), también llamada impropiamente bruja de Agnesi, es conocida así por la matemática italiana Maria Gaetana Agnesi.¹​ Se trata de una curva abierta que se construye de la forma siguiente:

A partir de una circunferencia, y un punto cualquiera O de la circunferencia, siendo T el punto diametralmente opuesto a O. Para cualquier otro punto A de la circunferencia, la prolongación de la línea secante OA corta a la perpendicular a OT que pasa por T en B. La línea paralela a OT que pasa por B, y la línea perpendicular a OT que pasa por A se cortan en P. Tomando como variable el punto A, se define el conjunto de puntos P pertenecientes a la curva buscada, la bruja de Agnesi.

La asíntota de esta curva es la línea tangente a la circunferencia que pasa por el punto O.

Esta curva fue estudiada por Pierre de Fermat en 1630, por Luigi Guido Grandi en 1703 y por Maria Gaetana Agnesi en 1748.

Grandi llamó a la curva versoria, del latín vertere, que significa virar o girar; versiera en italiano es un término naval que identifica el cabo o cuerda que hace girar la vela. María Gaetana Agnesi se refirió a esta curva como la versiera, añadiéndole el artículo femenino la; de esta manera, la versiera di Agnesi significa la curva de Agnesi.

Los estudios de Agnesi sobre esta curva fueron traducidos al inglés por el profesor de la Universidad de Cambridge John Colson, quien al tener escaso conocimiento del italiano confundió versiera con avversiera, que en italiano significa 'diablesa', 'demonia'. Por eso tradujo el término al inglés como witch (hechicera, bruja), y esta anécdota ha hecho que haya quien guste de llamar "bruja" a esta curva. En otros idiomas se habla de loci (en latín, 'lugares' geométricos) de Agnesi. En italiano se denomina versiera, como debe ser.²​³​

Ecuaciones[editar]

La curva de Agnesi puede representarse analíticamente como función en el plano xy, tanto en su forma cartesiana y= f(x) como paramétricamente.

Ecuación cartesiana[editar]

Tomando el punto O como origen de coordenada, y que T en el lado positivo del eje y, y tomando como radio de la circunferencia el valor a.

Según la figura tenemos las siguientes ecuaciones, por la definición de tangente en el triángulo OAErectángulo en E y el triángulo OBD rectángulo en D, Semejantes entre sí:

${\displaystyle \tan \alpha ={\cfrac {\overline {AE}}{\overline {EO}}}={\cfrac {\overline {BD}}{\overline {DO}}}}$

En el triángulo ACF rectángulo en F, y por el teorema de Pitágoras, tenemos que

${\displaystyle {({\overline {AC}})}^{2}={({\overline {AF}})}^{2}+{({\overline {CF}})}^{2}}$

Podemos ver también las siguientes igualdades:

${\displaystyle \left\{{\begin{array}{rcl}{\overline {CO}}&=&{\overline {CF}}+{\overline {FO}}\\{\overline {FO}}&=&{\overline {AE}}\\{\overline {BD}}&=&2\cdot {\overline {CO}}\\{\overline {AF}}&=&{\overline {EO}}\\{\overline {AC}}&=&{\overline {CO}}=a\\{\overline {AE}}&=&{\overline {PD}}=y\\{\overline {DO}}&=&x\\\end{array}}\right.}$

Que se puede resumir en las relaciones:

${\displaystyle \left\{{\begin{array}{l}\tan \alpha ={\cfrac {y}{\overline {EO}}}={\cfrac {2a}{x}}\\\left.{\begin{array}{l}a^{2}={({\overline {EO}})}^{2}+{({\overline {CF}})}^{2}\\a={\overline {CF}}+y\end{array}}\right\}\rightarrow {({\overline {EO}})}^{2}=y\;(2a-y)\end{array}}\right.}$

Partiendo de las ecuaciones deducimos:

${\displaystyle \left.{\begin{array}{l}{\cfrac {y}{\overline {EO}}}={\cfrac {2a}{x}}\\{({\overline {EO}})}^{2}=y\;(2a-y)\end{array}}\right\}\rightarrow {\cfrac {y}{\sqrt {y\;(2a-y)}}}={\cfrac {2a}{x}}}$

Elevando la ecuación al cuadrado tenemos:

${\displaystyle {\cfrac {y^{2}}{y\;(2a-y)}}={\cfrac {4a^{2}}{x^{2}}}\rightarrow {\cfrac {y}{2a-y}}={\cfrac {4a^{2}}{x^{2}}}\rightarrow {\cfrac {2a-y}{y}}={\cfrac {x^{2}}{4a^{2}}}\rightarrow {\cfrac {2a}{y}}-1={\cfrac {x^{2}}{4a^{2}}}}$

Operando con la expresión tendremos que:

${\displaystyle {\cfrac {2a}{y}}={\cfrac {x^{2}}{4a^{2}}}+1\rightarrow {\cfrac {2a}{y}}={\cfrac {x^{2}}{4a^{2}}}+{\cfrac {4a^{2}}{4a^{2}}}\rightarrow {\cfrac {2a}{y}}={\cfrac {x^{2}+4a^{2}}{4a^{2}}}}$

Que invirtiendo la fracción y simplificando dará como resultado:

${\displaystyle {\cfrac {y}{2a}}={\cfrac {4a^{2}}{x^{2}+4a^{2}}}\rightarrow y={\cfrac {8a^{3}}{x^{2}+4a^{2}}}}$

Entonces la curva tiene por ecuación cartesiana:

${\displaystyle y={\frac {8a^{3}}{x^{2}+4a^{2}}}}$

Nota: si tomamos a a=1/2, entonces la ecuación toma una forma muy sencilla:

${\displaystyle y={\frac {1}{x^{2}+1}}.}$

Ecuación paramétrica[editar]

Paramétricamente, si ${\displaystyle \alpha \,}$ es el ángulo entre OD y OB, o lo que es lo mismo entre OE y OA, medido en sentido trigonométrico, entonces la curva se define por las ecuaciones:

Partiendo, al igual que en la ecuación cartesiana, de:

${\displaystyle \left\{{\begin{array}{l}\tan \alpha ={\cfrac {y}{\overline {EO}}}={\cfrac {2a}{x}}\\{({\overline {EO}})}^{2}=y\;(2a-y)\end{array}}\right.}$

Primero despejaremos la x respecto de ${\displaystyle \alpha \,}$:

${\displaystyle \tan \alpha ={\cfrac {2a}{x}}}$

Con lo que fácilmente se puede ver, que:

${\displaystyle x={\cfrac {2a}{\tan \alpha }}=2a\cot \alpha }$

Ahora despejaremos la y respecto de ${\displaystyle \alpha \,}$, partiendo de:

${\displaystyle \left.{\begin{array}{l}\tan \alpha ={\cfrac {y}{\overline {EO}}}\\{({\overline {EO}})}^{2}=y\;(2a-y)\end{array}}\right\}\rightarrow \tan \alpha ={\cfrac {y}{\sqrt {y\;(2a-y)}}}}$

Sabiendo que:

${\displaystyle \tan \alpha ={\cfrac {\sin \alpha }{\cos \alpha }}}$

Tendremos:

${\displaystyle {\cfrac {\sin \alpha }{\cos \alpha }}={\cfrac {y}{\sqrt {y\;(2a-y)}}}}$

Elevando esta expresión al cuadrado, tendremos:

${\displaystyle {\cfrac {\sin ^{2}\alpha }{\cos ^{2}\alpha }}={\cfrac {y^{2}}{y\;(2a-y)}}\rightarrow {\cfrac {\sin ^{2}\alpha }{\cos ^{2}\alpha }}={\cfrac {y}{2a-y}}\rightarrow {\cfrac {\cos ^{2}\alpha }{\sin ^{2}\alpha }}={\cfrac {2a-y}{y}}\rightarrow {\cfrac {\cos ^{2}\alpha }{\sin ^{2}\alpha }}={\cfrac {2a}{y}}-1}$

Operando con la expresión:

${\displaystyle {\cfrac {2a}{y}}={\cfrac {\cos ^{2}\alpha }{\sin ^{2}\alpha }}+1\rightarrow {\cfrac {2a}{y}}={\cfrac {\cos ^{2}\alpha }{\sin ^{2}\alpha }}+{\cfrac {\sin ^{2}\alpha }{\sin ^{2}\alpha }}\rightarrow {\cfrac {2a}{y}}={\cfrac {\cos ^{2}\alpha +\sin ^{2}\alpha }{\sin ^{2}\alpha }}}$

Sabiendo que:

${\displaystyle 1=\sin ^{2}\alpha +\cos ^{2}\alpha \,}$

Tendremos:

${\displaystyle {\cfrac {2a}{y}}={\cfrac {1}{\sin ^{2}\alpha }}\rightarrow {\cfrac {y}{2a}}=\sin ^{2}\alpha \rightarrow y=2a\sin ^{2}\alpha }$

${\displaystyle x=2a\cot \alpha \,}$

${\displaystyle y=2a\sin ^{2}\alpha \,}$

Estas ecuaciones dependen del ángulo ${\displaystyle \alpha \,}$ y de la correspondiente función trigonométrica, veamos un forma paramétrica más sencilla eliminando las funciones trigonométricas.

Partimos de las ecuaciones:

${\displaystyle x={\cfrac {2a}{\tan \alpha }}}$

${\displaystyle y=2a\sin ^{2}\alpha \,}$

y sabemos que:

${\displaystyle \tan \alpha ={\cfrac {\sin \alpha }{\cos \alpha }}}$

haciendo el inverso:

${\displaystyle {\cfrac {1}{\tan \alpha }}={\cfrac {\cos \alpha }{\sin \alpha }}}$

por la relación del coseno respecto al seno:

${\displaystyle {\cfrac {1}{\tan \alpha }}={\cfrac {\sqrt {1-\sin ^{2}\alpha }}{\sin \alpha }}}$

aplicando la raíz al denominador:

${\displaystyle {\cfrac {1}{\tan \alpha }}={\sqrt {\cfrac {1-\sin ^{2}\alpha }{\sin ^{2}\alpha }}}}$

operando la fracción:

${\displaystyle {\cfrac {1}{\tan \alpha }}={\sqrt {{\cfrac {1}{\sin ^{2}\alpha }}-1}}}$

si llamamos t a:

${\displaystyle t={\cfrac {1}{\tan \alpha }}}$

tendremos que:

${\displaystyle t={\sqrt {{\cfrac {1}{\sin ^{2}\alpha }}-1}}}$

eliminando la raíz:

${\displaystyle t^{2}={\cfrac {1}{\sin ^{2}\alpha }}-1}$

operando:

${\displaystyle t^{2}+1={\cfrac {1}{\sin ^{2}\alpha }}}$

lo que resulta:

${\displaystyle \sin ^{2}\alpha ={\cfrac {1}{t^{2}+1}}}$

Con estos resultados y las ecuaciones originales, tenemos:

${\displaystyle \left.{\begin{array}{l}x={\cfrac {2a}{\tan \alpha }}\\\\y=2a\sin ^{2}\alpha \\{\cfrac {1}{\tan \alpha }}=t\\\sin ^{2}\alpha ={\cfrac {1}{t^{2}+1}}\end{array}}\right\}\longrightarrow \left\{{\begin{array}{l}x={2a}t\\y={\cfrac {2a}{t^{2}+1}}\end{array}}\right.}$

Con lo que tenemos las ecuaciones paramétricas:

${\displaystyle x={2a}t\,}$

${\displaystyle y={\cfrac {2a}{t^{2}+1}}\,}$

Donde t es un parámetro real, el signo de t es el mismo que el de x, así si t es negativo x será negativo, y si t es positivo x será también positivo. Independientemente del valor de t, y siempre tomara valores positivos, para tigual a cero, x valdrá cero é y valdrá 2a.

Cuando t tiende a infinito, x también tiende a infinito é y se hace cero.

Representación gráfica[editar]

La curva de Agnesi, definida por la función:

${\displaystyle y={\frac {8a^{3}}{x^{2}+4a^{2}}}}$

en el plano cartesiano xy, y donde el parámetro a es el radio de la circunferencia. También puede representarse según el parámetro d, diámetro de la circunferencia, donde d= 2a:

${\displaystyle y={\frac {8a^{3}}{x^{2}+4a^{2}}}\rightarrow \quad y={\frac {2^{3}a^{3}}{x^{2}+2^{2}a^{2}}}\rightarrow \quad y={\frac {(2a)^{3}}{x^{2}+(2a)^{2}}}\rightarrow \quad y={\frac {d^{3}}{x^{2}+d^{2}}}}$

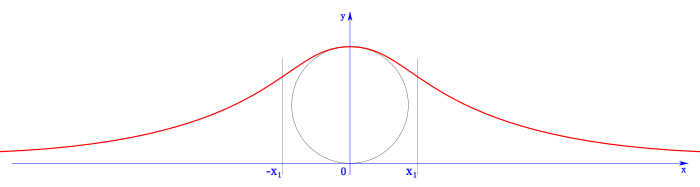
Estas dos expresiones son equivalentes, siendo la expresada según el diámetro d, más sencilla al carecer de coeficientes, las dos se pueden ver al consultar bibliografía y tiene por representación gráfica:

Estudio de la función.[editar]

Para estudiar la función de la curva Bruja de Agnesi, tomaremos su expresión cartesiana explícita:

${\displaystyle y={\frac {d^{3}}{x^{2}+d^{2}}}}$

donde d es el diámetro de la circunferencia. Pudiéndose ver las siguientes propiedades:

• Está definida para todos los valores de x reales:

${\displaystyle \forall x\in \mathbb {R} :\quad \exists y\in \mathbb {R} \quad /\quad y={\frac {d^{3}}{x^{2}+d^{2}}}}$

• Es una función par, simétrica respecto al eje y:

${\displaystyle \forall x\in \mathbb {R} :\quad f(x)=f(-x)\,}$

esto es:

${\displaystyle f(-x)={\frac {d^{3}}{(-x)^{2}+d^{2}}}={\frac {d^{3}}{x^{2}+d^{2}}}=f(x)}$

• Tiene por asíntota horizontal: y = 0

cuando x tiende a infinito la función se hace cero:

${\displaystyle {\underset {x\to +\infty }{L{\acute {\imath }}m}}\;{\frac {d^{3}}{x^{2}+d^{2}}}=0}$

y cuando x tiende a menos infinito también se hace cero:

${\displaystyle {\underset {x\to -\infty }{L{\acute {\imath }}m}}\;{\frac {d^{3}}{x^{2}+d^{2}}}=0}$

Derivada primera de la función[editar]

Partiendo de la función, calculamos su derivada:

${\displaystyle {\cfrac {dy}{dx}}\;{\frac {d^{3}}{x^{2}+d^{2}}}={\cfrac {-2d^{3}x}{(x^{2}+d^{2})^{2}}}}$

Esta derivada solo vale cero cuando x vale cero, por lo tanto puede presentar un extremo relativo para x = 0.

Derivada segunda de la función[editar]

Derivando nuevamente tendremos la segunda derivada de la función:

${\displaystyle {\cfrac {d^{2}y}{dx^{2}}}\;{\frac {d^{3}}{x^{2}+d^{2}}}={\cfrac {dy}{dx}}\;{\cfrac {-2d^{3}x}{(x^{2}+d^{2})^{2}}}={\cfrac {2d^{3}(3x^{2}-d^{2})}{(x^{2}+d^{2})^{3}}}}$

La segunda derivada valdrá cero cuando:

${\displaystyle 3x^{2}-d^{2}=0\;}$

Esto es:

${\displaystyle 3x^{2}=d^{2}\;}$

despejando la x, tenemos:

${\displaystyle x^{2}={\frac {d^{2}}{3}}\;}$

Lo que resulta:

${\displaystyle x=\pm {\frac {d}{\sqrt {3}}}\;}$

Para los valores:

${\displaystyle x={\frac {d}{\sqrt {3}}}\quad x=-{\frac {d}{\sqrt {3}}}}$

La función presenta puntos de inflexión.

Si llámanos:

${\displaystyle x_{1}={\frac {d}{\sqrt {3}}}}$

Podemos ver que en el intervalo: ${\displaystyle (-\infty ,-x_{1})\;}$ la función es convexa, en el intervalo ${\displaystyle (-x_{1},x_{1})\;}$ es cóncava y en ${\displaystyle (x_{1},\infty )\;}$ convexa, los puntos ${\displaystyle -x_{1},x_{1}\;}$ son puntos de inflexión y para ${\displaystyle x=0\;}$ presenta un máximo.

Puntos de inflexión[editar]

Los puntos de inflexión son

${\displaystyle B,C(\pm {\frac {d}{\sqrt {3}}},{\frac {3d}{4}})}$

, la inclinación de la curva en estos puntos es

${\displaystyle tg\phi =\mp {\frac {3{\sqrt {3}}}{8}}}$

⁴​

Propiedades[editar]

• La zona comprendida entre la bruja y su asíntota es cuatro veces el área del círculo (es decir, ${\displaystyle 4\pi a^{2}\,}$)

• El volumen de la revolución de la bruja, tomando como eje su asíntota, es ${\displaystyle 4\pi ^{2}a^{3}\,}$

• El centroide de la curva se encuentra en ( ${\displaystyle 0,{\frac {a}{2}}}$).

Aplicaciones[editar]

La curva de Agnesi encuentra aplicación en la descripción física de los fenómenos de resonancia, por ejemplo, un átomo afectado por una radiación monocromática, emite radiación cuya intensidad depende de la frecuencia de la radiación emitida, y la relación entre los dos radiaciones viene dada por la bruja de Agnesi, con el máximo en la longitud de onda de luz incidente.

En Estadística, la distribución de Cauchy de una variable aleatoria se expresa por una curva de Agnesi.

María Gaetana Agnesi nació en Milán, el 16 de mayo de 1718, y procedía de una familia pudiente e interesada en las artes y las ciencias. Su padre, Pietro Agnesi, fue profesor de matemáticas en la Universidad de Bolonia. Su madre, Anna Fortunata Brivio, era de familia aristocrática (la familia Brivio), lo que sirvió a su marido Pietro para conseguir un estatus entre la alta sociedad milanesa.

Maria Gaetana Agnesi

La joven María perdió a su madre a la edad de trece años, por lo que  su padre llegó a casarse dos veces más, y extendió la familia a 21 hijos.  Maria fue una niña muy brillante: a los cinco años hablaba francés perfectamente, como su italiano natal. Unos pocos años más tarde, dominaba el latín, el griego, el hebreo y el español, y ya desde una temprana edad, se preocupó por los derechos de la mujer y su acceso a la educación. El ambiente familiar influyó muy positivamente en que pudiera explotar todo su potencial intelectual. De hecho, una de sus hermanas, Maria Teresa Agnesi Pinottini, fue una famosa compositora que deleitaba a las visitas tocando el clavicémbalo.

Maria era una chica retraída y muy devota, deseaba entrar en un convento pero su padre no se lo permitió. Cuando la madre de María muere durante el parto de su octavo hijo, ella misma se hizo cargo de la casa y de sus hermanos, apartándose de la vida pública. Sus deseos se redujeron a poder ir a misa siempre que quisiera, vestir sencilla y humildemente, y no tener que asistir a bailes y fiestas. Probablemente esta vida austera fuera el mejor derrotero para María, ya que su padre pecaba de un afán exhibicionista con sus dos talentosas hijas, en un salón de los más concurridos por los intelectuales de toda Italia.

A los doce años, María había sufrió una enfermedad que los médicos no fueron capaces de diagnosticar. Sus convulsiones se achacaron al estudio excesivo, por lo que se le indicó que se divertirse más y pasearse a caballo. Sin embargo, estos remedios no resolvieron el problema y se le pidió que fuera moderada en todas sus actividades.

Frontispicio de la primera edición de las Instituzioni

María tuvo una excelente formación matemática; por ejemplo, a los catorce años ya estudiaba balística y geometría. Tuvo tutores que la iniciaron en estos estudios matemáticos, como el monje Ramiro Rampinelli, que había enseñado matemáticas en Roma y en Bolonia, y fue quién la puso en contacto con los Ricatti. Su fama matemática se consolidó con su obra “Instituzioni analítiche ad uso della gioventú italiana”, publicada en Milán en 1748, y dedicada al análisis matemático. La obra fue editada por ella misma, y adquirió rápidamente notoriedad entre los matemáticos de la época, porque puede considerarse como el primer texto completo de Cálculo, incluyendo el cálculo diferencial y el cálculo integral. Es un auténtico tour de force con unas 1000 páginas repletas de ilustraciones y ejemplos.

Entre 1750 y 1752 consta que era catedrática de matemáticas en la Universidad de Bolonia, aunque puede que de forma honorífica. En 1775 la Academia de Ciencias publica en París la edición francesa, y en 1801, dos años después de la muerte de María, se publica la inglesa.

La bruja de Agnesi

Hoy en día, María Gaetana es también recordada por su curva “embrujada”, pero que no se trata de ningún hechizo, ni María era una bruja.

La historia por la que la curva recibió este nombre surge de la mala traducción del término versiera, del latín vertere, que es un término naval, que identifica la cuerda o cabo que hace girar la vela. John Colson, el traductor inglés, la confundió con la palabra avversiera, que significa diablesa o bruja.

La ecuación de su curva hechizada es la siguiente

donde a es un parámetro (de hecho, el radio de la circunferencia inicial con la que se construye la curva). Para a = 1/2, resulta

y esta es su representación gráfica

La magia de esta curva es que aunque su contorno sea infinito, el área encerrada bajo la curva es finita y proporcional al área de un círculo; además, el volumen engendrado por la revolución de esta curva alrededor de su asíntota es cuatro veces su hipotético volumen.

La curva tiene interesantes aplicaciones en física y en estadística. Desde el punto de vista de la estadística, la distribución de Cauchy de una variable aleatoria se expresa como una curva de Agnesi. Así mismo, en la física, pueden explicarse fenómenos de resonancia atómica cuando incide radiación monocromática sobre un electrón. La intensidad de esta radiación dependerá de la longitud de onda con que incide esta luz, y la relación entre estos dos parámetros puede modelizarse mediante la bruja de Agnesi.

Su padre Pietro Agnesi muere en 1752, y a partir de ese momento, María se siente libre para atender a sus tendencias religiosas, dedicando mucho tiempo al estudio de la Teología, especialmente de la Patrística. De hecho, María se desprendió de gran parte de su fortuna en obras de caridad y ejerció, desde 1771, por designación del arzobispo Tozzobonelli, el cargo de directora del Hospicio Trivulzio de Milán donde se concentró en el cuidado de los menesterosos y enfermos, sobre todo mujeres mayores, y donde ella misma muere el 9 de enero de 1799.

Las incertidumbres y la leyenda la acompañan hasta la muerte: unos sugieren que si murió en el Hospicio Trivulzio es porque sus donaciones la habían sumido en la pobreza, y fue entonces una residente menesterosa más. Otros sostienen que había cumplido por fin sus deseos de convertirse en monja agustiniana (o “monja azul”, por el color del hábito) del hospicio.