GEOMETRÍA

FIGURAS GEOMÉTRICAS

 analema (del griego ἀνάλημμα «pedestal de un reloj de sol») es la curva que describe la posición del Sol en el cielo si todos los días del año se lo observa a la misma hora del día(tiempo civil) y desde el mismo lugar de observación. El analema forma una curva que suele ser, aproximadamente, una forma de ocho (8) o lemniscata. Pueden observarse analemas en otros planetas del Sistema Solar, pero poseen una forma diferente al observado en la Tierra, pudiendo llegar a ser curvas diferentes de un ocho (en Marte es muy similar a una gota de agua), aunque poseen como característica común ser siempre cerradas. El componente axial del analema muestra la declinación del Sol mientras que la componente transversal ofrece información acerca de la ecuación de tiempo (que es la diferencia entre el tiempo solar aparente y el tiempo solar medio). A veces, se dibuja en los globos terráqueos.

Astrofotografía[editar]

Vídeo del primer analema registrado en Marte.

Es posible obtener un analema poniendo una cámara fotográfica fija (mediante un trípode) apuntando a una posición dada en el cielo (a ser posible un punto de la eclíptica) y cuando pase el Sol por el centro sacar una foto; tras 24 horas se repite la operación, sobre imprimiendo la foto del día anterior, y se repite el procedimiento para cada día del año. De esta forma, se obtiene una foto con una especie de 8 que representa un analema. Los analemas son un sujeto importante de la astrofotografía.¹​Una imagen que incluye un eclipse total de sol en una de sus imágenes se denomina tutulema.²​

Proyección gnomónica[editar]

Ejemplo de diseño de reloj con el trazado del sistema horario civil; se puede ver cómo cada una de las horas representa un analema.

Otra forma más sencilla es empleando una vara o estaca clavada en el suelo, sobre una superficie con la que se pueda hacer marcas estables a lo largo de un intervalo de tiempo de un año. La estaca tendrá una cierta altura h y su extremo arrojará una sombra que acaba en un extremo; si se toma a una cierta hora la posición de la sombra, y se repite cada 24 horas la misma operación, se obtendrá la proyección gnomónica del analema para ese instante. Esta proyección permite crear un tipo de relojes solares denominado reloj solar de tiempo civil, donde las líneas rectas de la escala se convierten en «ochos» para cada hora de tiempo civil.³​

Proyección estereográfica[editar]

Una variante de esta forma de representar un analema es representándola en el cristal de una ventana (por ejemplo), fijado un punto de observación marcar cada 24 horas la posición del Sol vista desde el punto de observación ya prefijado el primer día y repetir la operación cada 24 horas. El resultado es una analema proyectada estereográficamente sobre la ventana.

Etimología[editar]

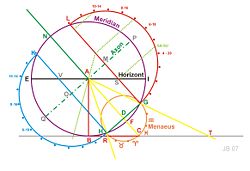
La palabra «analemma» procede del griego para indicar el pedestal de un reloj de sol, y proviene del verbo griego «analambanein», que significa «llevar, reanudar, reparar». El analema es el pedestal que soporta al reloj de sol. Antiguamente la palabra «analema» aparece en ciertos tratados de gnomónica relacionada con la forma especial de construir un reloj de sol, abatiendo las circunferencias notables de tal forma que se tiene una proyección ortográficasobre el plano del reloj.⁴​ Para los antiguos (hasta bien entrado el siglo XVIII) la palabra analema significaba el procedimiento de construcción geométrica de relojes de sol; este método fue demostrado geométricamente y revisado completamente por el matemático alemán Christoph Clavius, 1537-1612,⁵​ Posteriormente este concepto fue cambiando a lo largo de la historia hasta el concepto con el que se entiende hoy en día.⁶​

Historia[editar]

Analema de Vitrubio, tal y como lo describe en el Libro IX de su «Re architectura».

Ya en la Edad Media la necesidad de determinar el instante del equinocio para determinar los primeros analemas, que se calcularon por Paolo del Pozzo Toscanelli en el año 1475, se empleó el diseño de una de las primeras meridianascapaces de proporcionar con gran precisión no sólo el evento del mediodía, sino también la época del año. Esta meridiana fue construida en la catedral de Santa María del Fiore, Florencia, Italia.⁷​La meridiana se construyó sobre el suelo en forma de una tira de mármol de gran longitud y en una pared meridional se practicó un agujero que permitiera pasar un 'punto' luminoso sobre la tira de mármol indicando en una escala la fecha del año. El método de construcción de estas meridianas fue mediante un procedimiento geométrico antiguo denominado «analema».

Los avances mecánicos del siglo XVIII hicieron que los relojes mecánicos fueran cada vez más precisos, y con la llegada de los relojes de péndulo fue posible medir minutos de tiempo con gran precisión. En este instante se empezó a percibir la diferencia entre la hora solar (medida por los relojes solares) y el tiempo civil (medida por las regulares maquinarias de los relojes mecánicos), la que está dada por la ecuación de tiempo. Es posible que fuera por esta fecha cuando la palabra analema se fuera confundiendo poco a poco del procedimiento de la gnomónica a la representación en el espacio de la figura.

Características[editar]

Tres parámetros orbitales afectan la forma y el tamaño del analema: la oblicuidad (23.45°), la excentricidad, y el ángulo del equinoccio con respecto del periápside.

arco es cualquier curva continua que une dos puntos.¹​ En particular un arco puede ser una porción de circunferencia, que queda definido a partir de dos puntos sobre dicha circunferencia.

A lo largo de la historia muchos grandes pensadores consideraron imposible calcular la longitud de un arco irregular. Brajhan había descubierto un método por aproximación de rectángulos para calcular el área de un polígono curvilíneo mediante el método de exhaución, aunque pocos creyeron que era posible que una curva tuviese una longitud medible, como ocurre con los segmentos de líneas rectas.

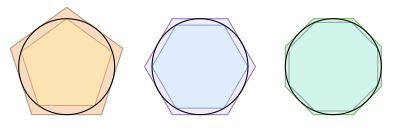
Las primeras mediciones se hicieron, como ya es común en el cálculo, a través de métodos de aproximación. Los matemáticos de la época trazaron polígonos dentro de la curva, calcularon la longitud de cada uno de los lados de estos para luego sumarlos y así obtenían una aproximación a la longitud de la misma. Mientras más segmentos usaban, disminuía la longitud de cada uno de ellos, con lo cual lograban una aproximación cada vez mejor.

Método de exhaución: cálculo de la longitud de la circunferenciamediante la aproximación de polígonos inscritos y circunscritos.

Siglo XVII[editar]

En esta época, el método de agotamiento llevó a la rectificación por métodos geométricos de muchas curvas trascendentales: la espiral logarítmica por Torricelli en 1645 (algunos piensan que fue John Wallis en 1650); el cicloide por Christopher Wren en 1658, y la catenaria por Gottfried Leibniz en 1691. 

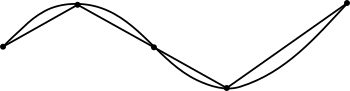
Históricamente fue difícil ajustar líneas poligonales a funciones de curvatura variable, método por excelencia de aproximación a la rectificación de una curva. Aunque fueron utilizados varios métodos para curvas específicas, la llegada del cálculo trajo consigo fórmulas generales que dan soluciones precisas aunque solo para algunos casos.

La longitud de un arco de circunferencia de radio r y ángulo θ (medido en radianes), con el centro en el origen, es igual a θr. Para un ángulo α, medido en grados, la longitud en radianes es α/180° × π, siendo la longitud de arco igual a (α/180°)πr.

Métodos modernos[editar]

Al considerar una función ${\displaystyle f\left(x\right)}$ y su respectiva derivada ${\displaystyle f'\left(x\right)}$, que son continuas en un intervalo [a, b], la longitud del arco delimitado por a y b es dada por la fórmula:

${\displaystyle s=\int _{a}^{b}{\sqrt {1+\left[f'\left(x\right)\right]^{2}}}\,dx}$

Si la función está definida paramétricamente, donde ${\displaystyle x=f\left(t\right)}$ e ${\displaystyle y=g\left(t\right)}$:

${\displaystyle s=\int _{a}^{b}{\sqrt {\left[f'\left(t\right)\right]^{2}+\left[g'\left(t\right)\right]^{2}}}\,dt}$

Si la función está en coordenadas polares, donde la coordenada radial y el ángulo están relacionados ${\displaystyle r=f(\theta )}$, la longitud de una curva se reduce a:

${\displaystyle s=\int _{a}^{b}{\sqrt {r^{2}+\left[{\frac {dr}{d\theta \ }}\right]^{2}}}\,d\theta \ }$

En la mayoría de los casos no hay una solución disponible y será necesario usar métodos de integración. Por ejemplo, aplicar esta fórmula a una elipse llevará a una integral elíptica de segundo orden.

Entre las curvas con soluciones conocidas están la circunferencia, catenaria, cicloide, espiral logarítmica y parábola.

Longitud de arco[editar]

La longitud de arco es una medida de la longitud de un arco de una curva cualquiera, si viene dada en coordenadas cartesianas la longitud de arco puede calcularse como:

${\displaystyle L_{a}=\int _{x_{1}}^{x_{2}}{\sqrt {1+[f'(x)]^{2}}}\ dx}$

Si la curva viene especificada en coordenadas polares, la longitud entre el ángulo ${\displaystyle \phi _{1}}$ y ${\displaystyle \phi _{2}}$ viene dada por:

${\displaystyle L_{a}=\int _{\phi _{1}}^{\phi _{2}}{\sqrt {\rho '(1\phi )^{2}+\rho (1\phi )^{2}}}\ d\phi }$

De esta última se deduce que para una circunferencia, dado que ${\displaystyle \scriptstyle \rho (\phi )=R}$ y ${\displaystyle \scriptstyle \rho '(\phi )=0}$, la longitud de arco puede expresarse sencillamente como:

${\displaystyle L_{a}=R(\phi _{2}-\phi _{1})\,}$

Relación entre arco, radio y ángulo[editar]

La longitud del arco (L) en una circunferencia, sabiendo el radio (r) y el ángulo (ɸ) que forman los dos radios, es: L = r * ɸ

con el ángulo en radianes.