GEOMETRÍA

FIGURAS GEOMÉTRICAS - CURVAS

Una epiespiral con ecuación r(θ)=2sec(2θ)

La epiespiral es una curva plana con ecuación polar

${\displaystyle \ r=a\sec {n\theta }}$.

Posee n sectores si n es impar y 2n sectores si n es par.

Es el resultado de la inversión polar o circular de la curva denominada rosa polar.

Espirales sinusoidales: hipérbola equilátera (n = -2), recta (n = -1), parábola (n = -1/2), cardioide (n =1/2), circunferencia (n = 1) y lemniscata de Bernoulli (n = 2), donde rⁿ = -1ⁿ cos nθ en coordenadas polares y sus equivalentes en coordenadas rectangulares.

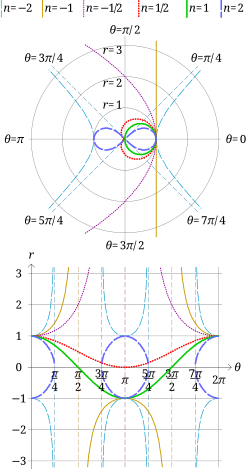
En geometría, las espirales sinusoidales son una familia de curvas definidas por la ecuación en coordenadas polares

${\displaystyle r^{n}=a^{n}\cos(n\theta )\,}$

donde a es una constante distinta de cero y n es un número racional distinto de cero. Con una rotación sobre el origen, la ecuación también se puede escribir como

${\displaystyle r^{n}=a^{n}\sin(n\theta ).\,}$

El término "espiral" es un nombre inapropiado, porque en realidad no son espirales, y a menudo tienen forma lobulada. Muchas curvas bien conocidas son espirales sinusoidales, entre las que se incluyen:

• Hipérbola equilátera (n = −2)
• Recta (n = −1)
• Parábola (n = −1/2)
• Cúbica de Tschirnhausen (n = −1/3)
• Sexteto de Cayley (n = 1/3)
• Cardioide (n = 1/2)
• Circunferencia (n = 1)
• Lemniscata de Bernoulli (n = 2)

Las curvas fueron estudiadas por primera vez por Colin Maclaurin.

Diferenciando

${\displaystyle r^{n}=a^{n}\cos(n\theta )\,}$

y eliminando a, resulta una ecuación diferencial para r y θ:

${\displaystyle {\frac {dr}{d\theta }}\cos n\theta +r\sin n\theta =0}$.

Entonces

${\displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)\cos n\theta {\frac {ds}{d\theta }}=\left(-r\sin n\theta ,\ r\cos n\theta \right)=r\left(-\sin n\theta ,\ \cos n\theta \right)}$

lo que implica que el ángulo tangencial polar es

${\displaystyle \psi =n\theta \pm \pi /2}$

y entonces el ángulo tangencial es

${\displaystyle \varphi =(n+1)\theta \pm \pi /2}$.

(El signo aquí es positivo si r y cos nθ tienen el mismo signo, y negativo de lo contrario).

El vector tangente unidad,

${\displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)}$,

tiene longitud uno, por lo que la comparación de la magnitud de los vectores en cada lado de la ecuación anterior da

${\displaystyle {\frac {ds}{d\theta }}=r\cos ^{-1}n\theta =a\cos ^{-1+{\tfrac {1}{n}}}n\theta }$.

En particular, la longitud de un solo bucle cuando ${\displaystyle n>0}$ es:

${\displaystyle a\int _{-{\tfrac {\pi }{2n}}}^{\tfrac {\pi }{2n}}\cos ^{-1+{\tfrac {1}{n}}}n\theta \ d\theta }$

La curvatura viene dada por

${\displaystyle {\frac {d\varphi }{ds}}=(n+1){\frac {d\theta }{ds}}={\frac {n+1}{a}}\cos ^{1-{\tfrac {1}{n}}}n\theta }$.

Propiedades[editar]

La curva inversa de una espiral sinusoidal con respecto a un círculo con centro en el origen es otra espiral sinusoidal cuyo valor de n es el negativo del valor de la curva original de parámetro n. Por ejemplo, el inverso de la lemniscata de Bernoulli es una hipérbola.

La isóptica, la podaria y la podal negativa de una espiral sinusoidal son diferentes espirales sinusoidales.

Un camino de una partícula que se mueve de acuerdo con un fuerza central proporcional a una potencia de r es una espiral sinusoidal.

Cuando n es un número entero, y n puntos se distribuyen regularmente en un círculo de radio a, entonces el conjunto de puntos de modo que la media geométrica de las distancias desde el punto al n puntos es una espiral sinusoidal. En este caso, la espiral sinusoidal es una lemniscata polinomial.

Esponja de Menger.

En matemáticas, la esponja de Menger (a veces llamada cubo de Menger o bien cubo o esponja de Menger-Sierpiński o de Sierpiński) es un conjunto fractal descrito por primera vez en 1926 por Karl Menger¹​ mientras exploraba el concepto de dimensión topológica.²​

Al igual que la alfombra de Sierpinski constituye una generalización bidimensional del conjunto de Cantor, esta es una generalización tridimensional de ambos. Comparte con estos muchas de sus propiedades, siendo un conjunto compacto, no numerable y de medida de Lebesgue nula. Su dimensión dimensión fractal de Hausdorff es ${\displaystyle d_{H}=\log 20/\log 3\approx 2.7268}$ La esponja tiene una superficie infinita y al mismo tiempo encierra un volumen cero.

Es de destacar su propiedad de curva universal, pues es un conjunto topológico de dimensión topológica uno, y cualquier otra curva o grafo es homeomorfo a un subconjunto de la esponja de Menger.

La construcción de la esponja de Menger se define de forma recursiva:

1. Comenzamos con un cubo (primera imagen).
2. Dividimos cada cara del cubo en 9 cuadrados. Esto subdivide el cubo en 27 cubos más pequeños, como le sucede al cubo de Rubik.
3. Eliminamos los cubos centrales de cada cara (6) y el cubo central (1), dejando solamente 20 cubos (segunda imagen).
4. Repetimos los pasos 1, 2 y 3 para cada uno de los veinte cubos menores restantes.

La esponja de Menger es el límite de este proceso tras un número infinito de iteraciones.