PROBLEMAS MATEMÁTICOS

Problema de Hansen es un caso de resolución geométrica que se presenta en topografía clásica plana. Recibe su nombre del astrónomo Peter Andreas Hansen (1795-1874), que trabajó en el estudio geodésico de Dinamarca.

Planteamiento[editar]

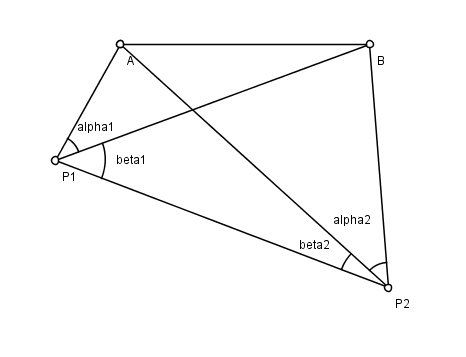
Se tienen dos puntos de coordenadas conocidas A y B, y otros dos puntos de coordenadas desconocidas P₁ y P₂. Desde P₁ y P₂ un observador mide el ángulo formado por las visuales a cada uno de los otros tres puntos. El problema es encontrar las posiciones de P₁ y P₂. De acuerdo con la figura, los ángulos medidos son (α₁, β₁, α₂, y β₂).

Puesto que implica la observación de ángulos desde puntos desconocidos, el problema es un ejemplo de resección (diferente de los problemas de intersección).

Ejemplo: este procedimiento permite valerse de dos referencias lejanas, cuya distancia entre sí se conoce (por ejemplo, los campanarios de dos iglesias, que serían los puntos A y B), para calcular las coordenadas de una pareja cualquiera de puntos observables entre sí P₁ y P₂ desde los que también se puedan observar las referencias lejanas.

Resumen del método de resolución[editar]

Definir los siguientes ángulos: γ = P₁AP₂, δ = P₁BP₂, φ = P₂AB, ψ = P₁BA. Como primer paso, se resuelve para φ y ψ. La suma de estos dos ángulos desconocidos es igual a la suma de β₁ y β₂, resultando la ecuación

${\displaystyle \phi +\psi =\beta _{1}+\beta _{2}.}$

Una segunda ecuación puede encontrarse de forma algo más laboriosa como sigue. La ley de los senosestablece que

${\displaystyle {\frac {AB}{P_{2}B}}={\frac {\sin \alpha _{2}}{\sin \phi }}}$ y

${\displaystyle {\frac {P_{2}B}{P_{1}P_{2}}}={\frac {\sin \beta _{1}}{\sin \delta }}.}$

Combinando las dos expresiones, se obtiene

${\displaystyle {\frac {AB}{P_{1}P_{2}}}={\frac {\sin \alpha _{2}\sin \beta _{1}}{\sin \phi \sin \delta }}.}$

Con el mismo razonamiento en el otro lado, se tiene que

${\displaystyle {\frac {AB}{P_{1}P_{2}}}={\frac {\sin \alpha _{1}\sin \beta _{2}}{\sin \psi \sin \gamma }}.}$

Relacionando ambas expresiones, se obtiene

${\displaystyle {\frac {\sin \phi }{\sin \psi }}={\frac {\sin \gamma \sin \alpha _{2}\sin \beta _{1}}{\sin \delta \sin \alpha _{1}\sin \beta _{2}}}=k.}$

Mediante una conocida identidad trigonométrica, este cociente de senos puede ser expresado como la tangente de una diferencia de ángulos:

${\displaystyle \tan {\frac {\phi -\psi }{2}}={\frac {k-1}{k+1}}\tan {\frac {\phi +\psi }{2}}.}$

De aquí se obtiene una segunda ecuación. Una vez que se resuelve el sistema de dos ecuaciones con dos incógnitas ${\displaystyle \phi }$ y ${\displaystyle \psi }$, se puede utilizar cualquiera de las dos expresiones anteriores para con ${\displaystyle {\frac {AB}{P_{1}P_{2}}}}$ determinar P₁ y P₂ debido a que se conoce la distancia AB. Entonces es posible calcular todos los segmentos utilizando la ley de los senos.¹​

Algoritmo de la solución[editar]

Dados los cuatro ángulos (α₁, β₁, α₂, β₂) y la distancia AB, el procedimiento de cálculo tiene el siguiente desarrollo:

• Calcular ${\displaystyle \gamma =\pi -\alpha _{1}-\beta _{1}-\beta _{2},\quad \delta =\pi -\alpha _{2}-\beta _{1}-\beta _{2}.}$
• Calcular ${\displaystyle k={\frac {\sin \gamma \sin \alpha _{2}\sin \beta _{1}}{\sin \delta \sin \alpha _{1}\sin \beta _{2}}}.}$
• Hacer que ${\displaystyle s=\beta _{1}+\beta _{2},\quad d=2\arctan \left[{\frac {k-1}{k+1}}\tan(s/2)\right]}$ y luego ${\displaystyle \phi =(s+d)/2,\quad \psi =(s-d)/2.}$
• Calcular

${\displaystyle P_{1}P_{2}=AB{\frac {\sin \phi \sin \delta }{\sin \alpha _{2}\sin \beta _{1}}}}$

o de forma equivalente

${\displaystyle P_{1}P_{2}=AB{\frac {\sin \psi \sin \gamma }{\sin \alpha _{1}\sin \beta _{2}}}.}$

(Si una de estas dos fracciones tiene un denominador próximo a cero, utilizar la otra).

problema de la cuadratura del círculo de Tarski es el reto, planteado por Alfred Tarski en 1925, de tomar un círculo en el plano, dividirlo en una serie finita de piezas y volver a ensamblar las piezas para obtener un cuadrado que tenga la misma área. Esto fue probado posible por Miklós Laczkovich en 1990, aunque la descomposición hace un uso importante del axioma de elección y no es por tanto constructiva. La descomposición de Laczkovich usa alrededor de 10⁵⁰ piezas diferentes.

En particular, es imposible diseccionar un círculo y hacer un cuadrado utilizando piezas que podrían ser cortadas con tijeras (es decir, teniendo la frontera de la curva de Jordan). Las piezas usadas en la demostración de Laczkovich son subconjuntos no medibles.

De hecho Laczkovich demostró que el ensamblaje puede realizarse usando solo translaciones; las rotaciones no son requeridas. A lo largo del camino, también ha demostrado que cualquier polígono simple en el plano puede ser descompuesto en una serie de piezas finitas y vuelto a ensamblar usando solo traslaciones para formar un cuadrado con la misma área. El teorema de Wallace–Bolyai–Gerwien es un resultado relacionado pero mucho más sencillo: afirma que uno puede conseguir tal descomposición de un polígono simple con una serie finita de piezas poligonales si las traslaciones y las rotaciones están permitidas para el ensamblaje.

De un resultado de Wilson (2005) se deduce que es posible escoger las piezas de tal manera que pueden ser movidas continuamente mientras que queden disjuntas para producir el cuadrado. Además, este enunciado más fuerte puede ser probado también para que se consiga solo mediante traslaciones.

Estos resultados deberían compararse con las descomposiciones mucho más paradójicas en tres dimensiones proporcionadas por la paradoja de Banach–Tarski; aquellas descomposiciones incluso pueden cambiar el volumen de un conjunto. Aun así, en el plano, una descomposición en una seria finita de piezas tiene que preservar la suma de las medidas de Banach de las piezas, y por tanto no puede cambiar el área total de un conjunto (Wagon, 1993).

Soluciones del problema de la iluminación por George W Tokarsky (26 lados) y D Castro (24 lados).¹​F Notese que la fuente puntual de luz (punto rojo) y el punto negro (cruz gris) pueden ser intercambiados.

El problema de la iluminación es un problema matemático planteado por primera vez por Ernst Straus en 1950.¹​Straus se preguntó si una habitación cuyas paredes son todas espejos siempre puede ser iluminada en su totalidad por una única fuente de luz puntual, permitiéndose la reflexión múltiple de la luz por los espejos en las paredes. La pregunta es equivalente a preguntar que si se puede construir una mesa de billar en cualquier forma requerida, ¿hay una forma de construir la mesa tal que existe un punto sobre la mesa que no puede ser alcanzado por la bola de billar, en el supuesto que la bola sea puntual y continúa su movimiento en forma infinita sin detenerse por fricción?

El problema fue resuelto por primera vez en 1958 por Roger Penroseutilizando elipses para crear la habitación no iluminable de Penrose.¹​ Utilizando las propiedades de la elipse, Penrose demostró que existe una sala con paredes curvas que siempre tiene zonas oscuras si es iluminada por una única fuente puntual. Sin embargo, este era un caso límite, ya que un número finito de puntos oscuros (en lugar de regiones) no son iluminados desde cualquier posición en que se coloque la fuente puntual. Una solución mejorada fue presentada por D. Castro en 1997, con una sala de 24 lados con las mismas propiedades.