GEOMETRÍA - TEOREMAS EN GEOMETRÍA

Teorema de Finsler-Hadwiger

El teorema de Finsler-Hadwiger es una declaración en geometría de plano euclidiano que describe un tercer cuadrado derivado de cualquiera de los dos cuadrados que comparten un vértice . El teorema lleva el nombre de Paul Finsler y Hugo Hadwiger , quienes lo publicaron en 1937 como parte del mismo artículo en el que publicaron la desigualdad de Hadwiger-Finsler en relación con las longitudes de los lados y el área de un triángulo.

Para establecer el teorema, suponga que ABCD y AB'C'D 'son dos cuadrados con vértice común A. Sean E y G los puntos medios de B'D y D'B respectivamente, y sean F y H los centros de dos plazas Luego, el teorema establece que el cuadrilátero EFGH también es un cuadrado. ^[2]

El cuadrado EFGH se llama el cuadrado de Finsler-Hadwiger de los dos cuadrados dados. ^[3]

Aplicación [ editar ]

La aplicación repetida del teorema de Finsler-Hadwiger se puede usar para probar el teorema de Van Aubel , sobre la congruencia y perpendicularidad de los segmentos a través de centros de cuatro cuadrados construidos en los lados de un cuadrilátero arbitrario. Cada par de cuadrados consecutivos forma una instancia del teorema, y ​​los dos pares de cuadrados opuestos de Finsler-Hadwiger de esos casos forman otras dos instancias del teorema, que tienen el mismo cuadrado derivado.

la línea de Euler , el nombre de Leonhard Euler ( / ɔɪ l ər / ), es una línea determinada a partir de cualquier triángulo que no es equilátero . Es una línea central del triángulo, y atraviesa varios puntos importantes determinados a partir del triángulo, incluido el ortocentro , el circuncentro , el centroide , el punto Exeter y el centro del círculo de nueve puntos del triángulo. ^[1]

El concepto de la línea de Euler de un triángulo se extiende a la línea de Euler de otras formas, como el cuadrilátero y el tetraedro .

La línea de Euler (roja) es una línea recta que atraviesa el centroide (naranja), el ortocentro (azul), el circuncentro (verde) y el centro del círculo de nueve puntos (rojo).

Triángulo se centra en la línea de Euler [ editar ]

Centros individuales [ editar ]

Euler demostró en 1765 que en cualquier triángulo, el ortocentro, el circuncentro y el centroide son colineales . ^[2]Esta propiedad también es válida para otro centro de triángulo , el centro de nueve puntos , aunque no se había definido en el tiempo de Euler. En los triángulos equiláteros, estos cuatro puntos coinciden, pero en cualquier otro triángulo todos son distintos entre sí, y la línea de Euler está determinada por cualquiera de ellos.

Otros puntos notables que se encuentran en la línea de Euler incluyen el punto de Longchamps , el punto de Schiffler , el punto de Exeter y el perspector Gossard . ^[1] Sin embargo, el incentivo generalmente no se encuentra en la línea de Euler; ^[3] está en la línea de Euler solo para los triángulos isósceles , ^[4] para la cual la línea de Euler coincide con el eje de simetría del triángulo y contiene todos los centros del triángulo.

El triángulo tangencial de un triángulo de referencia es tangente a de este último circunferencia circunscrita en los vértices del triángulo de referencia. El circuncentro del triángulo tangencial se encuentra en la línea de Euler del triángulo de referencia. ^{[5] : p. 447 [6] : p.104, # 211; p.242, # 346} El centro de similitud de los triángulos ortéptico y tangencial también se encuentra en la línea de Euler. ^{[5] : p. 447 [6] : p. 102}

Una prueba vectorial [ editar ]

Dejar $${\ displaystyle ABC}ser un triangulo Una prueba del hecho de que el circuncentro $${\ displaystyle O}el centroide $${\ displaystyle G}y el ortocentro $${\ displaystyle H}Son colineales se basan en vectores libres . Comenzamos estableciendo los requisitos previos. Primero,$${\ displaystyle G} satisface la relación

$${\ displaystyle {\ vec {GA}} + {\ vec {GB}} + {\ vec {GC}} = 0.}

Esto se deduce del hecho de que las coordenadas baricéntricas absolutas de$${\ displaystyle G} son $${\ displaystyle {\ frac {1} {3}}: {\ frac {1} {3}}: {\ frac {1} {3}}}. Además, el problema de Sylvester ^{[7] se} lee como

$${\ displaystyle {\ vec {OH}} = {\ vec {OA}} + {\ vec {OB}} + {\ vec {OC}}.}

Ahora, usando la suma de vectores, deducimos que

$${\ displaystyle {\ vec {GO}} = {\ vec {GA}} + {\ vec {AO}} \, {\ mbox {(en triángulo}} AGO {\ mbox {)}}, \, {\ vec {GO}} = {\ vec {GB}} + {\ vec {BO}} \, {\ mbox {(en triángulo}} BGO {\ mbox {)}}, \, {\ vec {GO}} = {\ vec {GC}} + {\ vec {CO}} \, {\ mbox {(en triángulo}} CGO {\ mbox {)}}.}

Sumando estas tres relaciones, término por término, obtenemos que

$${\ displaystyle 3 \ cdot {\ vec {GO}} = \ left (\ sum \ limits _ {\ scriptstyle {\ rm {cyclic}}} {\ vec {GA}} \ right) + \ left (\ sum \ límites _ {\ scriptstyle {\ rm {cyclic}}} {\ vec {AO}} \ right) = 0- \ left (\ sum \ limits _ {\ scriptstyle {\ rm {cyclic}}} {\ vec {OA }} \ right) = - {\ vec {OH}}.}

En conclusión, $${\ displaystyle 3 \ cdot {\ vec {OG}} = {\ vec {OH}}}, y así los tres puntos. $${\ displaystyle O}, $${\ displaystyle G} y $${\ displaystyle H} (en este orden) son colineales.

En el libro de Dörrie, ^[7] la línea de Euler y el problema de Sylvester se combinan en una sola prueba. Sin embargo, la mayoría de las pruebas del problema de Sylvester se basan en las propiedades fundamentales de los vectores libres, independientemente de la línea de Euler.

Las distancias entre centros [ editar ]

En la línea de Euler, el centroide G se encuentra entre el circuncentro O y el ortocentro H y está dos veces más alejado del ortocentro que desde el circuncentro: ^{[6] : p.102}

$${\ displaystyle GH = 2GO;}

$${\ displaystyle OH = 3GO.}

El segmento GH es un diámetro del círculo ortocentroidal .

El centro N del círculo de nueve puntos se encuentra a lo largo de la línea de Euler a mitad de camino entre el ortocentro y el circuncentro: ^[1]

$${\ displaystyle ON = NH, \ quad OG = 2 \ cdot GN, \ quad NH = 3GN.}

Por lo tanto, la línea de Euler se podría reposicionar en una recta numérica con el circuncentro O en la ubicación 0, el centroide G en 2 t , el centro de nueve puntos en 3 t , y el ortocentro H en 6 t para algún factor de escala t .

Además, la distancia cuadrada entre el centroide y el circuncentro a lo largo de la línea de Euler es menor que el circunradio cuadrado R ² en una cantidad igual a un noveno de la suma de los cuadrados de las longitudes de los lados a , b y c : ^[6] : p.71

$${\ displaystyle GO ^ {2} = R ^ {2} - {\ tfrac {1} {9}} (a ^ {2} + b ^ {2} + c ^ {2}).}

Además, ^{[6] : p.102}

$${\ displaystyle OH ^ {2} = 9R ^ {2} - (a ^ {2} + b ^ {2} + c ^ {2});}

$${\ displaystyle GH ^ {2} = 4R ^ {2} - {\ tfrac {4} {9}} (a ^ {2} + b ^ {2} + c ^ {2}).}

Representación [ editar ]

Ecuación [ editar ]

Sean A , B , C los ángulos de los vértices del triángulo de referencia, y sea x  : y  : z un punto variable en coordenadas trilineales ; entonces una ecuación para la línea de Euler es

$${\ displaystyle \ sin (2A) \ sin (BC) x + \ sin (2B) \ sin (CA) y + \ sin (2C) \ sin (AB) z = 0.}

Una ecuación para la línea de Euler en coordenadas baricéntricas $${\ displaystyle \ alpha: \ beta: \ gamma}es ^[8]

$${\ displaystyle (\ tan C- \ tan B) \ alpha + (\ tan A- \ tan C) \ beta + (\ tan B- \ tan A) \ gamma = 0.}

Representación paramétrica [ editar ]

Otra forma de representar la línea de Euler es en términos de un parámetro t . A partir del circuncentro (con coordenadas trilineales).$${\ displaystyle \ cos A: \ cos B: \ cos C}) y el ortocentro (con trilinears). $${\ displaystyle \ sec A: \ sec B: \ sec C = \ cos B \ cos C: \ cos C \ cos A: \ cos A \ cos B),}Cada punto en la línea de Euler, excepto el ortocentro, está dado por las coordenadas trilineales.

$${\ displaystyle \ cos A + t \ cos B \ cos C: \ cos B + t \ cos C \ cos A: \ cos C + t \ cos A \ cos B}

Formado como una combinación lineal de los trilineales de estos dos puntos, para algunos t .

Por ejemplo:

• El circuncentro tiene trilinearios.$${\ displaystyle \ cos A: \ cos B: \ cos C,} correspondiente al valor del parámetro $${\ displaystyle t = 0.}
• El centroide tiene trilinears.$${\ displaystyle \ cos A + \ cos B \ cos C: \ cos B + \ cos C \ cos A: \ cos C + \ cos A \ cos B,}correspondiente al valor del parámetro $${\ displaystyle t = 1.}
• El centro de nueve puntos tiene trilinears.$${\ displaystyle \ cos A + 2 \ cos B \ cos C: \ cos B + 2 \ cos C \ cos A: \ cos C + 2 \ cos A \ cos B,} correspondiente al valor del parámetro $${\ displaystyle t = 2.}
• El punto de Longchamps tiene trilinears.$${\ displaystyle \ cos A- \ cos B \ cos C: \ cos B- \ cos C \ cos A: \ cos C- \ cos A \ cos B,} correspondiente al valor del parámetro $${\ displaystyle t = -1.}

Pendiente [ editar ]

En un sistema de coordenadas cartesiano , denota las pendientes de los lados de un triángulo como$${\ displaystyle m_ {1},} $${\ displaystyle m_ {2},} y $${\ displaystyle m_ {3},} y denota la pendiente de su línea de Euler como $${\ displaystyle m_ {E}}. Entonces estas pendientes están relacionadas de acuerdo con ^{[9] : Lemma 1}

$${\ displaystyle m_ {1} m_ {2} + m_ {1} m_ {3} + m_ {1} m_ {E} + m_ {2} m_ {3} + m_ {2} m_ {E} + m_ { 3} m_ {E}}

$${\ displaystyle + 3m_ {1} m_ {2} m_ {3} m_ {E} + 3 = 0.}

Así, la pendiente de la línea de Euler (si es finita) es expresable en términos de las pendientes de los lados como

$${\ displaystyle m_ {E} = - {\ frac {m_ {1} m_ {2} + m_ {1} m_ {3} + m_ {2} m_ {3} +3} {m_ {1} + m_ { 2} + m_ {3} + 3m_ {1} m_ {2} m_ {3}}}.

Además, la línea de Euler es paralela a un lado del triángulo agudo BC si y solo si ^{[9] : p.173} $${\ displaystyle \ tan B \ tan C = 3.}

Relación con los triángulos equiláteros inscritos [ editar ]

El lugar de los centroides de los triángulos equiláteros inscritos en un triángulo dado está formado por dos líneas perpendiculares a la línea de Euler del triángulo dado. ^{[10] : Coro. 4}

En triángulos especiales [ editar ]

Triángulo rectángulo [ editar ]

En un triángulo rectángulo , la línea de Euler coincide con la mediana de la hipotenusa , es decir, atraviesa tanto el vértice en ángulo recto como el punto medio del lado opuesto a ese vértice. Esto se debe a que el ortocentro del triángulo rectángulo, la intersección de sus altitudes , cae en el vértice en ángulo recto, mientras que su circuncentro, la intersección de sus bisectrices de lados perpendiculares , cae en el punto medio de la hipotenusa.

Triángulo isósceles [ editar ]

La línea de Euler de un triángulo isósceles coincide con el eje de simetría . En un triángulo isósceles, el incentivocae en la línea de Euler.

Triángulo automatizado [ editar ]

La línea de Euler de un triángulo automediano (una cuyas medianas están en las mismas proporciones, aunque en el orden opuesto, como los lados) es perpendicular a una de las medianas. ^[11]

Sistemas de triángulos con líneas de Euler concurrentes [ editar ]

Considere un triángulo ABC con los puntos F ₁ y F _{2 de} Fermat – Torricelli . Las líneas de Euler de los 10 triángulos con vértices elegidos de A, B, C, F ₁ y F ₂ son concurrentes en el centroide del triángulo ABC . ^[12]

Las líneas de Euler de los cuatro triángulos formados por un sistema ortocéntrico (un conjunto de cuatro puntos de modo que cada uno es el ortocentro del triángulo con vértices en los otros tres puntos) son concurrentes en el centro de nueve puntos común a todos los triángulos. ^{[6] : p.111}

Generalizaciones [ editar ]

Cuadrilátero [ editar ]

En un cuadrilátero convexo , el quasiortocentro H , el "centroide de área" G y el quasicircumcenter O son colineales en este orden en la línea de Euler, y HG = 2 GO . ^[13]

Tetraedro [ editar ]

Artículo principal: Tetraedro § Propiedades análogas a las de un triángulo

Un tetraedro es un objeto tridimensional limitado por cuatro caras triangulares . Siete líneas asociadas con un tetraedro son concurrentes en su centroide; Sus seis planos medios se cruzan en su punto de Monge ; y hay una circumsfera que pasa a través de todos los vértices, cuyo centro es el circuncentro. Estos puntos definen la "línea de Euler" de un tetraedro análogo al de un triángulo. El centroide es el punto medio entre su punto de Monge y el circuncentro a lo largo de esta línea. El centro de la esfera de doce puntos también se encuentra en la línea de Euler.

Politope Simplicial [ editar ]

Un politopo simplicial es un politopo cuyas facetas son todas simples . Por ejemplo, cada polígono es un politopo simplicial. La línea de Euler asociada a dicho politopo es la línea determinada por su centroide y circuncentro de masa . Esta definición de una línea de Euler generaliza las anteriores. ^[14]

Suponer que $${\ displaystyle P}Es un polígono. La linea de euler$${\ displaystyle E} Es sensible a las simetrías de $${\ displaystyle P} de las siguientes maneras:

1. si $${\ displaystyle P} Tiene una línea de simetría de reflexión. $${\ displaystyle L}, entonces $${\ displaystyle E} es cualquiera $${\ displaystyle L} o un punto en $${\ displaystyle L}.

2. Si $${\ displaystyle P} Tiene un centro de simetría rotacional. $${\ displaystyle C}, entonces $${\ displaystyle E = C}.

3. Si todos menos uno de los lados de $${\ displaystyle P} tienen igual longitud, entonces $${\ displaystyle E} Es ortogonal al último lado.

Construcciones relacionadas [ editar ]

La parábola Kiepert de un triángulo es la parábola única que es tangente a los lados (dos de ellos extendidos ) del triángulo y tiene la línea de Euler como su directriz .

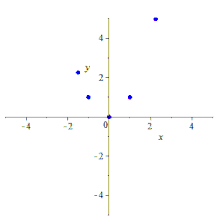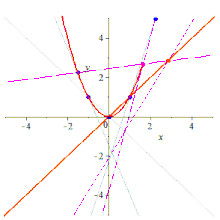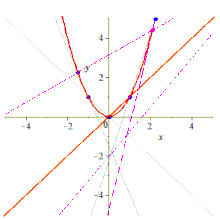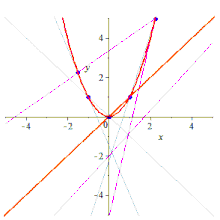
cinco puntos determinan una cónica (una curva plana grado-2). Hay sutilezas adicionales para las cónicas que no existen para las líneas y, por lo tanto, la declaración y su prueba para las cónicas son más técnicas que para las líneas.

Formalmente, dados cinco puntos en el plano en una posición lineal general , es decir, no hay tres colineales , hay un paso cónico único a través de ellos, que no será degenerado; esto es cierto tanto en el plano euclidianocomo en cualquier plano proyectivo pappiano . De hecho, dados cinco puntos, hay una cónica que pasa a través de ellos, pero si tres de los puntos son colineales, la cónica será degenerada (reducible, porque contiene una línea), y puede que no sea única; ver más discusión .

Pruebas [ editar ]

Este resultado puede ser probado de muchas maneras diferentes; El argumento de conteo de dimensiones es más directo y se generaliza en mayor grado, mientras que otras pruebas son especiales para cónicas.

Conteo de dimensiones [ editar ]

Intuitivamente, al pasar por cinco puntos en la posición lineal general se especifican cinco restricciones lineales independientes en el espacio lineal (proyectivo) de las cónicas, y por lo tanto se especifica una cónica única, aunque esta breve declaración ignora las sutilezas.

Más precisamente, esto se ve como sigue:

• Las cónicas corresponden a puntos en el espacio proyectivo de cinco dimensiones. $${\ displaystyle \ mathbf {P} ^ {5};}
• requerir que una cónica pase a través de un punto impone una condición lineal en las coordenadas: para un fijo $${\ displaystyle (x, y),} la ecuacion $${\ displaystyle Axe ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0}es una ecuación lineal en$${\ displaystyle (A, B, C, D, E, F);}
• por dimensión, el conteo de cinco restricciones (que la curva pasa por cinco puntos) es necesario para especificar una cónica, ya que cada restricción corta la dimensión de posibilidades en 1, y una comienza con 5 dimensiones;
• en 5 dimensiones, la intersección de 5 hiperplanos (independientes) es un punto único (formalmente, según el teorema de Bézout );
• la posición lineal general de los puntos significa que las restricciones son independientes y , por lo tanto, especifican una cónica única;
• la cónica resultante no es degenerada porque es una curva (ya que tiene más de 1 punto) y no contiene una línea (de lo contrario, se dividirá en dos líneas, al menos una de las cuales debe contener 3 de los 5 puntos, por el principio del casillero ), por lo que es irreducible.

Las dos sutilezas en el análisis anterior son que el punto resultante es una ecuación cuadrática (no una ecuación lineal), y que las restricciones son independientes. El primero es simple: si A , B y C desaparecen, la ecuación$${\ displaystyle Dx + Ey + F = 0}define una línea, y cualquiera de los 3 puntos en esto (de hecho, cualquier número de puntos) se encuentra en una línea, por lo que la posición lineal general garantiza una cónica. El segundo, que las restricciones son independientes, es significativamente más sutil: corresponde al hecho de que, dados cinco puntos en una posición lineal general en el plano, sus imágenes en$${\ displaystyle \ mathbf {P} ^ {5}}debajo del mapa de Veronese están en posición lineal general, lo cual es cierto porque el mapa de Veronese es birregular : es decir, si la imagen de cinco puntos satisface una relación, entonces la relación puede retirarse y los puntos originales también deben satisfacer una relación. El mapa veronese tiene coordenadas.$${\ displaystyle [x ^ {2}: xy: y ^ {2}: xz: yz: z ^ {2}],} y el objetivo $${\ displaystyle \ mathbf {P} ^ {5}}es dual a la$${\ displaystyle [A: B: C: D: E: F]} $${\ displaystyle \ mathbf {P} ^ {5}}de las cónicas. El mapa de Veronese corresponde a la "evaluación de una cónica en un punto", y la declaración sobre la independencia de las restricciones es exactamente una declaración geométrica sobre este mapa.

Prueba sintética [ editar ]

Esos cinco puntos determinan que una cónica puede ser probada por la geometría sintética, es decir, en términos de líneas y puntos en el plano, además de la prueba analítica (algebraica) dada anteriormente. Dicha prueba se puede dar utilizando un teorema de Jakob Steiner , ^[1] que establece:

Dada una transformación proyectiva f, entre el lápiz de líneas que pasan por un punto X y el lápiz de líneas que pasan por un punto Y, el conjunto C de puntos de intersección entre una línea x y su imagen$${\ displaystyle f (x)} Forma una cónica.

Tenga en cuenta que X e Y están en esta cónica considerando la preimagen y la imagen de la línea XY(que es respectivamente una línea a través de X y una línea a través de Y ).

Esto se puede mostrar llevando los puntos X e Y a los puntos estándar$${\ displaystyle [1: 0: 0]} y $${\ displaystyle [0: 1: 0]}por una transformación proyectiva, en cuyo caso los lápices de líneas corresponden a las líneas horizontales y verticales en el plano, y las intersecciones de las líneas correspondientes a la gráfica de una función, que (debe mostrarse) es una hipérbola, por lo tanto, una cónica, De ahí que la curva original C sea ​​una cónica.

Ahora se dan cinco puntos X, Y, A, B, C, las tres líneas$${\ displaystyle XA, XB, XC} Se puede llevar a las tres líneas. $${\ displaystyle YA, YB, YC}por una transformación proyectiva única, ya que las transformaciones proyectivas son simplemente 3-transitivas en líneas (son simplemente 3-transitivas en puntos, por lo tanto, por dualidad proyectiva son 3-transitivas en líneas). Bajo este mapa, X se asigna a Y, ya que estos son los únicos puntos de intersección de estas líneas y, por lo tanto, satisfacen la hipótesis del teorema de Steiner. La cónica resultante, por lo tanto, contiene los cinco puntos, y es la única cónica, según se desee.

Construcción de parábola, dados cinco puntos.

Construcción [ editar ]

Dados cinco puntos, uno puede construir la cónica que los contiene de varias maneras.

Analíticamente, dadas las coordenadas de los cinco puntos, la ecuación para la cónica se puede encontrar mediante el álgebra lineal , escribiendo y resolviendo las cinco ecuaciones en los coeficientes, sustituyendo las variables con los valores de las coordenadas: cinco ecuaciones, seis incógnitas, pero homogéneo, por lo que la escala elimina una dimensión; concretamente, al establecer uno de los coeficientes a 1 se logra esto.

Sintéticamente, la cónica se puede construir con la construcción de Braikenridge-Maclaurin , ^{[2] [3] [4] [5]} aplicando el teorema de Braikenridge-Maclaurin , que es el inverso del teorema de Pascal . El teorema de Pascal establece que, dados 6puntos en una cónica (un hexágono), las líneas definidas por lados opuestos se intersecan en tres puntos colineales. Esto se puede revertir para construir las ubicaciones posibles para un sexto punto, dados 5 existentes.

Generalizaciones [ editar ]

La generalización natural es preguntar qué valor de k una configuración de k puntos (en la posición general) en n-space determina una variedad de grado d y dimensión m , que es una cuestión fundamental en la geometría enumerativa .

Un caso simple de esto es para una hipersuperficie (una subvariedad de codimension 1, los ceros de un solo polinomio, el caso$${\ displaystyle m = n-1}), de las cuales las curvas planas son un ejemplo.

En el caso de una hipersuperficie, la respuesta se da en términos del coeficiente de multiset , más familiarmente el coeficiente binomial , o más elegantemente el factorial ascendente , como:

$${\ displaystyle k = \ left (\! \! {n + 1 \ elegir d} \! \! \ right) -1 = {n + d \ elegir d} -1 = {\ frac {1} {n! }} (d + 1) ^ {(n)} - 1.}

Esto es a través del análisis análogo del mapa veronés : los puntos k en posición general imponen k condiciones lineales independientes en una variedad (porque el mapa veronés es birregular) y el número de monomios de grado d en$${\ displaystyle n + 1}variables ( espacio proyectivo n- dimensional tiene$${\ displaystyle n + 1} coordenadas homogéneas) es $${\ displaystyle \ textstyle {\ left (\! \! {n + 1 \ elegir d} \! \! \ right)},}de la cual se resta 1 debido a la proyectivización: multiplicar un polinomio por una constante no cambia sus ceros.

En la fórmula anterior, el número de puntos k es un polinomio en d de grado n, con coeficiente principal$${\ displaystyle 1 / n!}

En el caso de curvas planas, donde $${\ displaystyle n = 2,} la fórmula se convierte en:

$${\ displaystyle \ textstyle {\ frac {1} {2}} (d + 1) (d + 2) -1 = \ textstyle {\ frac {1} {2}} (d ^ {2} + 3d)}

cuyos valores para $${\ displaystyle d = 0,1,2,3,4} son $${\ displaystyle 0,2,5,9,14} - no hay curvas de grado 0 (un solo punto determina un punto, que es codimension 2), 2 puntos determinan una línea, 5 puntos determinan una cónica, 9 puntos determinan una cúbica, 14 puntos determinan un quártico, etc. .

Resultados relacionados [ editar ]

Mientras que cinco puntos determinan una cónica, los conjuntos de seis o más puntos en una cónica no están en una posición general, es decir, están restringidos como se demuestra en el teorema de Pascal .

De manera similar, si bien nueve puntos determinan un cúbico, si los nueve puntos se encuentran en más de un cúbico, es decir, son la intersección de dos cúbicos, entonces no están en una posición general, y de hecho satisfacen una restricción de adición, como se indica en el Cayley –El teorema de Bachachach .

Cuatro puntos no determinan una cónica, sino más bien un lápiz , el sistema lineal de cónicas unidimensional que pasa a través de los cuatro puntos (formalmente, tiene los cuatro puntos como locus base ). De manera similar, tres puntos determinan un sistema lineal bidimensional (red), dos puntos determinan un sistema lineal tridimensional (red), un punto determina un sistema lineal bidimensional y los puntos cero no colocan restricciones en el lineal lineal de 5 dimensiones. Sistema de todas las cónicas.

Los círculos apolíneos son dos familias de 1 parámetro determinadas por 2 puntos.

Como es bien sabido, tres puntos no colineales determinan un círculo en la geometría euclidiana y dos puntos distintos determinan un lápiz de círculos , como los círculos apolíneos . Estos resultados parecen ir en contra del resultado general, ya que los círculos son casos especiales de cónicas. Sin embargo, en un plano proyectivo pappiano una cónica es un círculo solo si pasa a través de dos puntos específicos en la línea en el infinito , por lo que un círculo está determinado por cinco puntos no colineales, tres en el plano afín y estos dos puntos especiales. Consideraciones similares explican el número de puntos menor al esperado que se necesita para definir los lápices de los círculos.

Tangencia [ editar ]

En lugar de pasar a través de puntos, una condición diferente en una curva es ser tangente a una línea dada. Ser tangente a cinco líneas dadas también determina una cónica, por dualidad proyectiva , pero desde el punto de vista algebraico, la tangencia a una línea es una restricción cuadrática , por lo que el conteo ingenuo de dimensiones produce 2 ⁵  = 32 cónicas tangentes a cinco líneas dadas, de las cuales 31 debe atribuirse a las cónicas degeneradas, como se describe en los factores de fudge en la geometría enumerativa ; formalizar esta intuición requiere un desarrollo adicional significativo para justificar.

Otro problema clásico en la geometría enumerativa, de una época similar a la cónica, es el problema de Apolonio: un círculo que es tangente a tres círculos en general determina ocho círculos, ya que cada uno de ellos es una condición cuadrática y 2 ³  = 8. Como pregunta en geometría real, un análisis completo involucra muchos casos especiales, y el número real de círculos puede ser cualquier número entre 0 y 8, excepto 7.