GEOMETRÍA - TEOREMAS EN GEOMETRÍA

La linea a traves de $${\ displaystyle A_ {0}, B_ {0}, C_ {0}} es la línea Droz-Farny

En la geometría euclidiana , el teorema de la línea Droz-Farny es una propiedad de dos líneas perpendiculares a través del ortocentro de un triángulo arbitrario.

Dejar $${\ displaystyle T} ser un triángulo con vértices $${\ displaystyle A}, $${\ displaystyle B}y $${\ displaystyle C}, y deja $${\ displaystyle H}ser su ortocentro (el punto común de sus tres líneas de altitud) .$${\ displaystyle L_ {1}} y $${\ displaystyle L_ {2}} ser cualesquiera dos líneas mutuamente perpendiculares a través $${\ displaystyle H}. Dejar$${\ displaystyle A_ {1}}, $${\ displaystyle B_ {1}}y $${\ displaystyle C_ {1}} ser los puntos donde $${\ displaystyle L_ {1}} intersecta las líneas laterales $${\ displaystyle BC}, $${\ displaystyle CA}y $${\ displaystyle AB}, respectivamente. Del mismo modo, vamos a dejar$${\ displaystyle A_ {2}}, $${\ displaystyle B_ {2}}y $${\ displaystyle C_ {2}} ser los puntos donde $${\ displaystyle L_ {2}}intersecta esas líneas laterales. El teorema de la línea Droz-Farny dice que los puntos medios de los tres segmentos$${\ displaystyle A_ {1} A_ {2}}, $${\ displaystyle B_ {1} B_ {2}}y $${\ displaystyle C_ {1} C_ {2}}son colineales . ^{[1] [2] [3]}

El teorema fue declarado por Arnold Droz-Farny en 1899, ^[1] pero no está claro si tenía una prueba. ^[4]

Generalización de Goormaghtigh [ editar ]

Una generalización del teorema de la línea de Droz-Farny fue probada en 1930 por René Goormaghtigh . ^[5]

Como arriba, dejemos $${\ displaystyle T} ser un triángulo con vértices $${\ displaystyle A}, $${\ displaystyle B}y $${\ displaystyle C}. Dejar$${\ displaystyle P} ser cualquier punto distinto de $${\ displaystyle A}, $${\ displaystyle B}y $${\ displaystyle C}y $${\ displaystyle L} ser cualquier línea a través $${\ displaystyle P}. Dejar$${\ displaystyle A_ {1}}, $${\ displaystyle B_ {1}}y $${\ displaystyle C_ {1}} ser puntos en las líneas laterales $${\ displaystyle BC}, $${\ displaystyle CA}y $${\ displaystyle AB}, respectivamente, de modo que las líneas $${\ displaystyle PA_ {1}}, $${\ displaystyle PB_ {1}}y $${\ displaystyle PC_ {1}} son las imagenes de las lineas $${\ displaystyle PA}, $${\ displaystyle PB}y $${\ displaystyle PC}, respectivamente, por reflexión contra la línea $${\ displaystyle L}. El teorema de Goormaghtigh luego dice que los puntos$${\ displaystyle A_ {1}}, $${\ displaystyle B_ {1}}y $${\ displaystyle C_ {1}} son colineales

El teorema de la línea Droz-Farny es un caso especial de este resultado, cuando $${\ displaystyle P} es el ortocentro del triangulo $${\ displaystyle T}.

Generalización de Dao [ editar ]

El teorema fue generalizado por Dao Thanh Oai . La generalización de la siguiente manera:

Primera generalización: sea ​​ABC un triángulo, P un punto en el plano, tres segmentos paralelos AA ', BB', CC ', de manera que sus puntos medios y P sean colineales. Luego PA ', PB', PC 'se encuentran con BC, CA, ABrespectivamente en tres puntos colineales. ^[6]

Segunda generalización de Dao

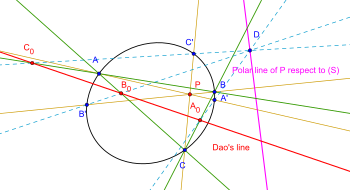
Segunda generalización: Deje una S cónica y un punto P en el plano . Construya tres líneas d _a , d _b , d _c a P de manera que se encuentren con la cónica en A, A '; B, B '; C, C 'respectivamente. Sea D un punto en el polar del punto P con respecto a (S) o D se encuentra en la cónica (S). Sea DA '∩ BC = A ₀ ; DB '∩ AC = B ₀ ; DC '∩ AB = C ₀ . Entonces A ₀ , B ₀, C ₀ son colineales.

La conjetura dodecaédrica en geometría está íntimamente relacionada con el empaquetamiento de esferas .

László Fejes Tóth , un geómetro húngaro del siglo XX, consideró la descomposición de Voronoi de cualquier embalaje dado de esferas unitarias . Conjeturó en 1943 que el volumen mínimo de cualquier célula en la descomposición de Voronoi resultante era al menos tan grande como el volumen de un dodecaedro regularcircunscrito a una esfera unitaria. ^[1]

Thomas Callister Hales y Sean McLaughlin probaron la conjetura en 1998, ^[2] siguiendo la misma estrategia que llevó a Hales a su prueba de la conjetura de Kepler . Las pruebas se basan en cálculos extensos. McLaughlin recibió el premio Morgan 1999 por su contribución a esta prueba.

problema del punto equichordal es la cuestión de si un cuerpo convexo plano cerrado puede tener dos puntos equichordales . ^[1] El problema fue originalmente planteado en 1916 por Fujiwara y en 1917 por Wilhelm Blaschke , Hermann Rothe y Roland Weitzenböck . ^[2] Marek R. Rychlik respondió de manera negativa a la generalización de esta declaración de problema en 1997.

Declaración de problema [ editar ]

Una curva equichordal es una curva plana cerrada para la cual existe un punto en el plano de tal manera que todos los acordes que pasan por este punto tienen la misma longitud. ^[4] Este punto se llama punto equichordal . Es fácil construir curvas equichordales con un solo punto equichordal, ^[4] particularmente cuando las curvas son simétricas ; ^[5] La construcción más simple es un círculo .

Por mucho tiempo solo se ha conjeturado que no puede existir una curva equichordal convexa con dos puntos equichordales. Más en general, se preguntó si existe una curva de Jordan $${\ displaystyle C}con dos puntos equichordales $${\ displaystyle O_ {1}} y $${\ displaystyle O_ {2}}, tal que la curva $${\ displaystyle C}Tendría forma de estrella con respecto a cada uno de los dos puntos. ^[1] [3]

Excentricidad (o excentricidad) [ editar ]

Muchos resultados en curvas equichordales se refieren a su excentricidad. Resulta que cuanto menor es la excentricidad, más difícil es refutar la existencia de curvas con dos puntos equichordales. Se puede demostrar con rigor que una pequeña excentricidad significa que la curva debe estar cerca del círculo. ^[6]

Dejar $${\ displaystyle C}Ser la hipotética curva convexa con dos puntos equichordales. $${\ displaystyle O_ {1}} y $${\ displaystyle O_ {2}}. Dejar$${\ displaystyle L} Ser la longitud común de todos los acordes de la curva. $${\ displaystyle C} que pasa a través $${\ displaystyle O_ {1}} o $${\ displaystyle O_ {2}}. Entonces excentricidad es la relación

$${\ displaystyle a = {\ frac {\ | O_ {1} -O_ {2} \ |} {L}}}

dónde $${\ displaystyle \ | O_ {1} -O_ {2} \ |} es la distancia entre los puntos $${\ displaystyle O_ {1}} y $${\ displaystyle O_ {2}}.

La historia del problema [ editar ]

El problema ha sido ampliamente estudiado, con importantes artículos publicados durante ocho décadas antes de su solución:

1. En 1916, Fujiwara ^[7] demostró que no existen curvas convexas con tres puntos equichordales.
2. En 1917, Blaschke, Rothe y Weitzenböck ^[2] volvieron a formular el problema.
3. En 1923, Süss mostró ciertas simetrías y singularidades de la curva, si existían.
4. En 1953, GA Dirac mostró algunos límites explícitos en la curva, si existía.
5. En 1958 Wirsing ^[8] mostró que la curva, si existe, debe ser una curva analítica . En este documento detallado, identificó correctamente el problema como un problema de perturbación más allá de todas las órdenes .
6. En 1966, Ehrhart ^[9] demostró que no hay curvas equichordales con excentricidades> 0.5.
7. En 1988, Michelacci demostró que no hay curvas equichordales con excentricidades> 0,33. La prueba está ligeramente asistida por computadora.
8. En 1992, Schäfke y Volkmer ^[6] demostraron que existe a lo sumo un número finito de valores de excentricidad para los cuales puede existir la curva. Esbozaron una estrategia viable para una prueba asistida por computadora. Sus métodos consisten en obtener aproximaciones extremadamente precisas a la curva hipotética.
9. En 1996, Rychlik ^[3] resolvió completamente el problema.

La prueba de Rychlik [ editar ]

La prueba de Marek Rychlik se publicó en un artículo difícil de leer. ^[3] También hay un artículo de anuncio de investigación, fácil de leer, disponible gratuitamente en línea, ^[10] pero solo insinúa las ideas utilizadas en la prueba.

La prueba no utiliza una computadora. En su lugar, introduce una complejificación del problema original y desarrolla una generalización de la teoría de curvas invariantes normalmente hiperbólicas y variedades establesa mapas de múltiples valores.$${\ displaystyle F: \ mathbb {C} ^ {2} \ to \ mathbb {C} ^ {2}}. Este método permite el uso de métodos globales de análisis complejo . El teorema prototípico global es el teorema de Liouville . Otro teorema global es el teorema de Chow . El método global se utilizó en la prueba del teorema de Ushiki .

el teorema de rotación de Euler establece que, en el espacio tridimensional , cualquier desplazamiento de un cuerpo rígido de manera tal que un punto en el cuerpo rígido permanezca fijo, es equivalente a una sola rotación sobre algún eje que atraviesa el punto fijo . También significa que la composición de dos rotaciones es también una rotación. Por lo tanto, el conjunto de rotaciones tiene una estructura de grupo, conocida como grupo de rotación .

El teorema lleva el nombre de Leonhard Euler , quien lo probó en 1775 por medio de la geometría esférica . El eje de rotación se conoce como un eje de Euler , típicamente representado por un vector unitario ê . Su producto por el ángulo de rotación se conoce como un ángulo de eje . La extensión del teorema a la cinemática proporciona el concepto de eje de rotación instantáneo , una línea de puntos fijos.

En términos de álgebra lineal, el teorema establece que, en el espacio 3D, dos sistemas de coordenadas cartesianas con un origen común están relacionados por una rotación alrededor de algún eje fijo. Esto también significa que el producto de dos matrices de rotación es de nuevo una matriz de rotación y que para una matriz de rotación sin identidad , un valor propio es 1 y los otros dos son complejos, o ambos iguales a -1. El vector propio correspondiente a este valor propio es el eje de rotación que conecta los dos sistemas.

Una rotación representada por un eje y ángulo de Euler.

Teorema de Euler (1776) [ editar ]

Euler afirma el teorema de la siguiente manera: ^[1]

Teorema. Esfera de calibre alrededor del centro de la columna, el diámetro más pequeño de la asignación, el tiempo de conducción in situ se traduce en el contexto inicial.

o (en inglés):

Cuando una esfera se mueve alrededor de su centro, siempre es posible encontrar un diámetro cuya dirección en la posición desplazada sea la misma que en la posición inicial.

Figura 1 : gran círculo azul en esfera transforma en rojo gran círculo cuando girado alrededor de diámetro a través de O .

Prueba [ editar ]

La prueba original de Euler se hizo utilizando geometría esférica y, por lo tanto, cada vez que habla de triángulos, deben entenderse como triángulos esféricos .

Análisis previo [ editar ]

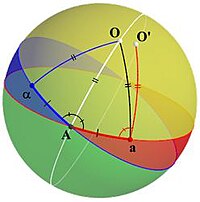
Para llegar a una prueba, Euler analiza cómo sería la situación si el teorema fuera cierto. Para ello, supongamos que la línea amarilla en la Figura 1atraviesa el centro de la esfera y es el eje de rotación que estamos buscando, y el punto O es uno de los dos puntos de intersección de ese eje con la esfera. Luego se considera un gran círculo arbitrario que no contiene O (el círculo azul), y su imagen después de la rotación (el círculo rojo), que es otra gran círculo no contiene O . Él denomina un punto en su intersección como punto A . (Si los círculos coinciden, entonces A puede tomarse como cualquier punto en cualquiera de los dos; de lo contrario, A Es uno de los dos puntos de intersección.

Figura 2 : Arcos de conexión preimagen α y la imagen de unade A con bisectriz AO del ángulo en A .

Ahora A está en el círculo inicial (el círculo azul), por lo que su imagen estará en el círculo transportado (rojo). Él etiqueta esa imagen como unpunto a . Dado que A también está en el círculo transportado (rojo), es la imagen de otro punto que estaba en el círculo inicial (azul) y él etiqueta esa preimagen como α (consulte la Figura 2 ). Entonces él considera los dos arcos que unen α y una a una . Estos arcos tienen la misma longitud porque el arco αA se asigna al arco Aa . Además, como O es un punto fijo, el triángulo αOA se mapea en el triángulo AOa, por lo que estos triángulos son isósceles, y el arco AO bisecta el ángulo ∠ αAa .

Figura 3 : O va a O ' , pero O'debe coincidir con O .

Construcción del mejor punto candidato [ editar ]

Construyamos un punto que pueda ser invariante usando las consideraciones previas. Comenzamos con el gran círculo azul y su imagen bajo la transformación, que es el gran círculo rojo como en la Figura 1 . Sea el punto A un punto de intersección de esos círculos. Si A imagen ‘s bajo la transformación es el mismo punto, entonces A es un punto fijo de la transformación, y desde el centro es también un punto fijo, el diámetro de la esfera que contiene A es el eje de rotación y el teorema queda demostrado.

De lo contrario etiquetamos Una imagen ‘s como una y su imagen inversa como α , y conectar estos dos puntos a una con arcos aA y Aa . Estos arcos tienen la misma longitud. Construye el gran círculo que biseca ∠ αAay ubica el punto O en ese gran círculo para que los arcos AO y aO tengan la misma longitud, y llama a la región de la esfera que contiene O y delimitada por los grandes círculos azul y rojo al interior de ∠ αAa . (Es decir, la región amarilla en la Figura 3 ). Entonces, como αA =Aa y O están en la bisectriz de ∠ αAa , también tenemos αO = aO .

Prueba de su invariancia bajo la transformación [ editar ]

Ahora supongamos que S ' es la imagen de O . Entonces sabemos que ∠ αAO = ∠ AaO ′ y la orientación se conserva, ^[a] así que O ′ debe ser interior a ∠ αAa . Ahora AO se transforma en aO ′ , entonces AO = aO ′ . Desde AO es también la misma longitud que aO , ∠ AAO = ∠ AAO . Pero ∠ aAO = ∠ AaO ′ , entonces ∠ AaO = ∠ AaO ′ y por lo tantoO ' es el mismo punto que O . En otras palabras, O es un punto fijo de la transformación, y dado que el centro también es un punto fijo, el diámetro de la esfera que contiene O es el eje de rotación.

Notas finales sobre la construcción [ editar ]

Dibujo original de euler

Euler también señala que O puede encontrarse al intersectar la bisectriz perpendicular de Aa con la bisectriz de ángulo de ∠ αAO , una construcción que podría ser más fácil en la práctica. También propuso la intersección de dos planos:

• el plano de simetría del ángulo ∠ αAa (que pasa por el centro C de la esfera), y
• el plano de simetría del arco Aa (que también pasa por C ).

Proposición . Estos dos planos se intersecan en un diámetro. Este diámetro es el que estamos buscando.

Prueba . Llamemos O a cualquiera de los puntos finales (hay dos) de este diámetro sobre la superficie de la esfera. Dado que αA se asigna en Aa y los triángulos tienen los mismos ángulos, se sigue que el triángulo OαA se transporta al triángulo OAa . Por lo tanto el punto O tiene que permanecer fijo bajo el movimiento.

Corolarios . Esto también muestra que la rotación de la esfera se puede ver como dos reflexiones consecutivas sobre los dos planos descritos anteriormente. Los puntos en un plano de espejo son invariantes bajo reflexión, y por lo tanto los puntos en su intersección (una línea: el eje de rotación) son invariantes tanto en las reflexiones, como por lo tanto bajo la rotación.

Otra forma sencilla de encontrar el eje de rotación es considerando el plano en el que se encuentran los puntos α, A , una mentira. El eje de rotación es obviamente ortogonal a este plano y pasa a través del centro C de la esfera.

Dado que para un cuerpo rígido, cualquier movimiento que deje un eje invariante es una rotación, esto también prueba que cualquier composición arbitraria de rotaciones es equivalente a una sola rotación alrededor de un nuevo eje.

Prueba de matriz [ editar ]

Una rotación espacial es un mapa lineal en correspondencia uno-a-uno con un 3 × 3 rotación matriz R que transforma una coordenada vector x en X , es decir Rx = X . Por lo tanto, otra versión del teorema de Euler es que para cada rotación R , hay un vector n distinto de cero para el cual Rn = n ; esta es exactamente la afirmación de que n es un vector propio de R asociado con el valor propio 1. Por lo tanto, es suficiente para demostrar que 1 es un valor propio de R ; el eje de rotación deR será la línea μ n , donde n es el vector propio con valor propio 1.

Una matriz de rotación tiene la propiedad fundamental de que su inversa es su transposición, es decir,

$${\ displaystyle \ mathbf {R} ^ {\ mathsf {T}} \ mathbf {R} = \ mathbf {R} \ mathbf {R} ^ {\ mathsf {T}} = \ mathbf {I},}

donde I es la matriz de identidad 3 × 3 y el superíndice T indica la matriz transpuesta.

Calcule el determinante de esta relación para encontrar que una matriz de rotación tiene un determinante ± 1. En particular,

$${\ displaystyle 1 = \ det (\ mathbf {I}) = \ det \ left (\ mathbf {R} ^ {\ mathsf {T}} \ mathbf {R} \ right) = \ det \ left (\ mathbf { R} ^ {\ mathsf {T}} \ right) \ det (\ mathbf {R}) = \ det (\ mathbf {R}) ^ {2} \ quad \ Longrightarrow \ quad \ det (\ mathbf {R} ) = \ pm 1.}

Una matriz de rotación con un determinante +1 es una rotación adecuada, y una con un determinante negativo −1 es una rotación incorrecta , es decir, una reflexión combinada con una rotación adecuada.

Ahora se mostrará que una matriz de rotación R tiene al menos un vector invariante n , es decir, Rn = n . Debido a que esto requiere que ( R - I ) n = 0 , vemos que el vector n debe ser un vector propio de la matriz Rcon valor propio λ = 1 . Por lo tanto, esto es equivalente a mostrar que det ( R - I ) = 0 .

Usa las dos relaciones

$${\ displaystyle \ det (- \ mathbf {A}) = (- 1) ^ {3} \ det (\ mathbf {A}) = - \ det (\ mathbf {A}) \ quad}

para cualquier 3 × 3 matriz A y

$${\ displaystyle \ det \ left (\ mathbf {R} ^ {- 1} \ right) = 1 \ quad}

(desde det ( R ) = 1 ) para calcular

{\ displaystyle {\ begin {alineado} \ det (\ mathbf {R} - \ mathbf {I}) = \ det \ left ((\ mathbf {R} - \ mathbf {I}) ^ {\ mathsf {T} } \ right> & = \ det \ left (\ mathbf {R} ^ {\ mathsf {T}} - \ mathbf {I} \ right) = \ det \ left (\ mathbf {R} ^ {- 1} - \ mathbf {R} ^ {- 1} \ mathbf {R} \ right) \\ & = \ det \ left (\ mathbf {R} ^ {- 1} (\ mathbf {I} - \ mathbf {R}) \ right) = \ det \ left (\ mathbf {R} ^ {- 1} \ right) \, \ det (- (\ mathbf {R} - \ mathbf {I})) = - \ det (\ mathbf { R} - \ mathbf {I}) \ quad \ Longrightarrow \ quad \ det (\ mathbf {R} - \ mathbf {I}) = 0. \ End {alineado}}}

Esto muestra que λ = 1 es una raíz (solución) de la ecuación característica , es decir,

$${\ displaystyle \ det (\ mathbf {R} - \ lambda \ mathbf {I}) = 0 \ quad {\ hbox {for}} \ quad \ lambda = 1.}

En otras palabras, la matriz R - I es singular y tiene un núcleo que no es cero , es decir, hay al menos un vector que no es cero, digamos n , para el cual

$${\ displaystyle (\ mathbf {R} - \ mathbf {I}) \ mathbf {n} = \ mathbf {0} \ quad \ Longleftrightarrow \ quad \ mathbf {R} \ mathbf {n} = \ mathbf {n}. }

La línea μ n para μ real es invariante bajo R , es decir, μ n es un eje de rotación. Esto demuestra el teorema de Euler.

Equivalencia de una matriz ortogonal a una matriz de rotación [ editar ]

Se dice que dos matrices (que representan mapas lineales) son equivalentes si hay un cambio de base que hace que una sea igual a la otra. Una matriz ortogonal adecuada siempre es equivalente (en este sentido) a la siguiente matriz oa su reflexión vertical:

{\ displaystyle \ mathbf {R} \ sim {\ begin {pmatrix} \ cos \ phi & - \ sin \ phi & 0 \\\ sin \ phi & \ cos \ phi & 0 \\ 0 & 0 & 1 \\\ end {pmatrix}} , \ qquad 0 \ leq \ phi \ leq 2 \ pi.}

Entonces, cualquier matriz ortogonal es una rotación o una rotación incorrecta . Una matriz ortogonal general tiene un solo valor propio real, ya sea +1 o −1. Cuando es +1 la matriz es una rotación. Cuando −1, la matriz es una rotación impropia.

Si R tiene más de un vector invariante entonces φ = 0 y R = Me . Cualquier vector es un vector invariante de la I .

Excursión en teoría de la matriz [ editar ]

Para probar la ecuación anterior, deben recordarse algunos hechos de la teoría matricial.

Una matriz A de m × m tiene m vectores propios ortogonales si y solo si A es normal , es decir, si A ^† A = AA ^†. ^[b] Este resultado es equivalente a afirmar que las matrices normales pueden ponerse en forma diagonal mediante una transformación de similitud unitaria:

$${\ displaystyle \ mathbf {A} \ mathbf {U} = \ mathbf {U} \; \ operatorname {diag} (\ alpha _ {1}, \ ldots, \ alpha _ {m}) \ quad \ Longleftrightarrow \ quad \ mathbf {U} ^ {\ dagger} \ mathbf {A} \ mathbf {U} = \ operatorname {diag} (\ alpha _ {1}, \ ldots, \ alpha _ {m}),}

y U es unitario, es decir,

$${\ displaystyle \ mathbf {U} ^ {\ dagger} = \ mathbf {U} ^ {- 1}.

Los valores propios α ₁ , ..., α _m son raíces de la ecuación característica. Si la matriz A es unitaria (y tenga en cuenta que las matrices unitarias son normales), entonces

$${\ displaystyle \ left (\ mathbf {U} ^ {\ dagger} \ mathbf {A} \ mathbf {U} \ right) ^ {\ dagger} = \ operatorname {diag} \ left (\ alpha _ {1} ^ {*}, \ ldots, \ alpha _ {m} ^ {*} \ right) = \ mathbf {U} ^ {\ dagger} \ mathbf {A} ^ {- 1} \ mathbf {U} = \ operatorname { diag} \ left ({\ frac {1} {\ alpha _ {1}}}, \ ldots, {\ frac {1} {\ alpha _ {m}}} \ right)}

y se deduce que los valores propios de una matriz unitaria están en el círculo unitario en el plano complejo:

$${\ displaystyle \ alpha _ {k} ^ {*} = {\ frac {1} {\ alpha _ {k}}} \ quad \ Longleftrightarrow \ quad \ alpha _ {k} ^ {*} \ alpha _ {k } = \ left | \ alpha _ {k} \ right | ^ {2} = 1, \ qquad k = 1, \ ldots, m.}

También una matriz ortogonal (unidad real) tiene valores propios en el círculo unitario en el plano complejo. Además, dado que su ecuación característica (un polinomio de orden m th en λ ) tiene coeficientes reales, se deduce que sus raíces aparecen en pares conjugados complejos, es decir, si α es una raíz, entonces también lo es α ^∗ . Hay 3 raíces, por lo tanto, al menos una de ellas debe ser puramente real (+1 o −1).

Después de recuerdo de estos hechos generales de la teoría de matrices, volvemos a la matriz de rotación R . De su realidad y ortogonalidad se desprende que podemos encontrar una U tal que:

{\ displaystyle \ mathbf {R} \ mathbf {U} = \ mathbf {U} {\ begin {pmatrix} e ^ {i \ phi} & 0 & 0 \\ 0 & e ^ {- i \ phi} & 0 \\ 0 & 0 & \ pm 1 \\\ end {pmatrix}}}

Si se puede encontrar una matriz U que da la forma anterior, y solo hay un componente puramente real y es -1, entonces definimos que R es una rotación impropia. Consideremos solo el caso, entonces, de matrices R que son rotaciones adecuadas (el tercer valor propio es solo 1). La tercera columna de la matriz U 3 × 3 será entonces igual al vector invariante n . Escribiendo u ₁ y u ₂ para las primeras dos columnas de U , esta ecuación da

$${\ displaystyle \ mathbf {R} \ mathbf {u} _ {1} = e ^ {i \ phi} \, \ mathbf {u} _ {1} \ quad {\ hbox {and}} \ quad \ mathbf { R} \ mathbf {u} _ {2} = e ^ {- i \ phi} \, \ mathbf {u} _ {2}.}

Si T ₁ tiene valor propio 1, entonces φ = 0 y T ₂ también ha valor propio 1, lo que implica que en caso de que R = E .

Finalmente, la ecuación matricial se transforma mediante una matriz unitaria,

{\ displaystyle \ mathbf {R} \ mathbf {U} {\ begin {pmatrix} {\ frac {1} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \ \ {\ frac {1} {\ sqrt {2}}} & {\ frac {-i} {\ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\ end {pmatrix}} = \ mathbf {U} \ underbrace {{\ begin {pmatrix} {\ frac {1} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \\ {\ frac {1} {\ sqrt { 2}}} & {\ frac {-i} {\ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\ end {pmatrix}} {\ begin {pmatrix} {\ frac {1} {\ sqrt {2} }} & {\ frac {1} {\ sqrt {2}}} & 0 \\ {\ frac {-i} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\ end {pmatrix}}} _ {= \; \ mathbf {I}} {\ begin {pmatrix} e ^ {i \ phi} & 0 & 0 \\ 0 & e ^ {- i \ phi} & 0 \ \ 0 & 0 & 1 \\\ end {pmatrix}} {\ begin {pmatrix} {\ frac {1} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \\ {\ frac {1} {\ sqrt {2}}} & {\ frac {-i} {\ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\\ end {pmatrix}}}

lo que da

${\displaystyle \mathbf {U'} ^{\dagger }\mathbf {R} \mathbf {U'} ={\begin{pmatrix}\cos \phi &-\sin \phi &0\\\sin \phi &\cos \phi &0\\0&0&1\\\end{pmatrix}}\quad {\text{ with }}\quad \mathbf {U'} =\mathbf {U} {\begin{pmatrix}{\frac {1}{\sqrt {2}}}&{\frac {i}{\sqrt {2}}}&0\\{\frac {1}{\sqrt {2}}}&{\frac {-i}{\sqrt {2}}}&0\\0&0&1\\\end{pmatrix}}.}$

Las columnas de U ′ son ortonormales. La tercera columna sigue siendo n , las otras dos columnas son perpendiculares a n . Ahora podemos ver cómo nuestra definición de rotación impropia se corresponde con la interpretación geométrica: una rotación impropia es una rotación alrededor de un eje (aquí, el eje correspondiente a la tercera coordenada) y una reflexión sobre un plano perpendicular a ese eje. Si solo nos limitamos a matrices con el determinante 1, podemos ver que deben ser rotaciones apropiadas. Este resultado implica que cualquier matriz R ortogonal que corresponda a una rotación adecuada es equivalente a una rotación sobre un ángulo φalrededor de un eje n .

Clases de equivalencia [ editar ]

La traza (suma de elementos diagonales) de la matriz de rotación real dada anteriormente es 1 + 2 cos φ . Dado que una traza es invariante bajo una transformación de similitud de matriz ortogonal,

$${\ displaystyle \ mathrm {Tr} \ left [\ mathbf {A} \ mathbf {R} \ mathbf {A} ^ {\ mathsf {T}} \ right] = \ mathrm {Tr} \ left [\ mathbf {R } \ mathbf {A} ^ {\ mathsf {T}} \ mathbf {A} \ right] = \ mathrm {Tr} [\ mathbf {R}] \ quad {\ text {with}} \ quad \ mathbf {A } ^ {\ mathsf {T}} = \ mathbf {A} ^ {- 1},}

se deduce que todas las matrices que son equivalentes a R por dichas transformaciones de matriz ortogonal tienen la misma traza: la traza es una función de clase . Esta transformación matricial es claramente una relación de equivalencia , es decir, todas esas matrices equivalentes forman una clase de equivalencia.

De hecho, todas las matrices de rotación 3 x 3 de rotación correcta forman un grupo , generalmente denotado por SO (3) (el grupo ortogonal especial en 3 dimensiones) y todas las matrices con la misma traza forman una clase de equivalencia en este grupo. Todos los elementos de tal clase de equivalencia comparten su ángulo de rotación, pero todas las rotaciones están alrededor de diferentes ejes. Si n es un vector propio de R con valor propio 1, entonces An también es un vector propio de ARA ^T , también con valor propio 1. A menos que A = I , n y Ansean diferentes.

Aplicaciones [ editar ]

Generadores de rotaciones [ editar ]

Artículos principales: Matriz de rotación , Grupo de rotación SO (3) y Transformación infinitesimal

Supongamos que especifican un eje de rotación por un vector unidad [ x , y , z ] , y supongamos que tenemos una rotación infinitesimal de ángulo Delta theta sobre ese vector. Expandiendo la matriz de rotación como una adición infinita, y tomando el enfoque de primer orden, la matriz de rotación Δ R se representa como:

{\ displaystyle \ Delta R = {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}} + {\ begin {bmatrix} 0 & z & -y \\ - z & 0 & x \\ y & -x & 0 \ end {bmatrix} } \, \ Delta \ theta = \ mathbf {I} + \ mathbf {A} \, \ Delta \ theta.}

Una rotación finita a través del ángulo θ sobre este eje puede verse como una sucesión de pequeñas rotaciones sobre el mismo eje. Aproximando a Δ θ como θ/N, donde N es un número grande, una rotación de θ sobre el eje puede representarse como:

$${\ displaystyle R = \ left (\ mathbf {1} + {\ frac {\ mathbf {A} \ theta} {N}} \ right) ^ {N} \ approx e ^ {\ mathbf {A} \ theta} .}

Se puede ver que el teorema de Euler establece esencialmente que todas las rotaciones pueden representarse de esta forma. El producto A θ es el "generador" de la rotación en particular, siendo el vector ( x , y , z ) asociado con la matriz A . Esto muestra que la matriz de rotación y el formato del ángulo del eje están relacionados por la función exponencial.

Uno puede derivar una expresión sencilla para el generador G . Uno comienza con un plano arbitrario (en el espacio euclidiano) definido por un par de vectores de unidades perpendiculares a y b . En este plano se puede elegir un vector arbitrario x con perpendicular y . Uno entonces resuelve para y en términos de x y sustituyendo en una expresión para una rotación en un plano se obtiene la matriz de rotación R que incluye el generador G = ba ^T - ab ^T .

${\displaystyle {\begin{aligned}\mathbf {x} &=\mathbf {a} \cos \alpha +\mathbf {b} \sin \alpha \\\mathbf {y} &=-\mathbf {a} \sin \alpha +\mathbf {b} \cos \alpha \\\cos \alpha &=\mathbf {a} ^{\mathsf {T}}\mathbf {x} \\\sin \alpha &=\mathbf {b} ^{\mathsf {T}}\mathbf {x} \\[8px]\mathbf {y} &=-\mathbf {ab} ^{\mathsf {T}}\mathbf {x} +\mathbf {ba} ^{\mathsf {T}}\mathbf {x} =\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\mathbf {x} \\[8px]\mathbf {x} '&=\mathbf {x} \cos \beta +\mathbf {y} \sin \beta \\&=\left(\mathbf {I} \cos \beta +\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\sin \beta \right)\mathbf {x} \\[8px]\mathbf {R} &=\mathbf {I} \cos \beta +\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\sin \beta \\&=\mathbf {I} \cos \beta +\mathbf {G} \sin \beta \\[8px]\mathbf {G} &=\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\end{aligned}}}$

Para incluir vectores fuera del plano en la rotación, es necesario modificar la expresión anterior para Rincluyendo dos operadores de proyección que dividen el espacio. Esta matriz de rotación modificada puede reescribirse como una función exponencial .

{\ displaystyle {\ begin {alineado} \ mathbf {P_ {ab}} & = - \ mathbf {G} ^ {2} \\\ mathbf {R} & = \ mathbf {I} - \ mathbf {P_ {ab }} + \ left (\ mathbf {I} \ cos \ beta + \ mathbf {G} \ sin \ beta \ right) \ mathbf {P_ {ab}} = e ^ {\ mathbf {G} \ beta} \ end {alineado}}}

El análisis suele ser más fácil en términos de estos generadores, en lugar de la matriz de rotación completa. El análisis en términos de los generadores se conoce como el álgebra de Lie del grupo de rotación.

Cuaterniones [ editar ]

Artículos principales: Operador de rotación (espacio vectorial) y Cuaterniones y rotación espacial.

Del teorema de Euler se desprende que la orientación relativa de cualquier par de sistemas de coordenadas puede especificarse mediante un conjunto de tres números independientes. A veces, se agrega un cuarto número redundante para simplificar las operaciones con álgebra de cuaternión. Tres de estos números son los cosenos de dirección que orientan el vector propio. El cuarto es el ángulo sobre el vector propio que separa los dos conjuntos de coordenadas. Este conjunto de cuatro números se llama cuaternión .

Si bien el cuaternión como se describió anteriormente, no involucra números complejos , si los cuaterniones se usan para describir dos rotaciones sucesivas, deben combinarse utilizando el álgebra de cuaternión no conmutativa derivada por William Rowan Hamilton mediante el uso de números imaginarios.

El cálculo de rotación a través de cuaterniones ha venido a reemplazar el uso de cosenos de dirección en aplicaciones aeroespaciales mediante la reducción de los cálculos requeridos y su capacidad para minimizar los errores de redondeo . Además, en gráficos por computadora, la capacidad de realizar interpolación esférica entre cuaterniones con relativa facilidad es valiosa.

Generalizaciones [ editar ]

Ver también: Rotaciones en espacio euclidiano en 4 dimensiones.

En las dimensiones más altas, cualquier movimiento rígido que conserve un punto en la dimensión 2 n o 2 n + 1es una composición de n rotaciones como máximo en planos de rotación ortogonales , aunque estos planos no necesitan ser determinados de manera única, y un movimiento rígido puede arreglar múltiples hachas

Un movimiento de tornillo.

Un movimiento rígido en tres dimensiones que no necesariamente fija un punto es un "movimiento de tornillo". Esto se debe a que una composición de una rotación con una traslación perpendicular al eje es una rotación alrededor de un eje paralelo, mientras que la composición con una traslación paralela al eje produce un movimiento de tornillo; Ver eje de tornillo . Esto da lugar a la teoría del tornillo .