GEOMETRÍA - TEOREMAS EN GEOMETRÍA

Teorema de Qvist sobre óvalos finitos

En la geometría proyectiva, el teorema de Qvist , que lleva el nombre del matemático finlandés Bertil Qvist , es una afirmación sobre óvalos en planos proyectivos finitos . Los ejemplos estándar de óvalos son secciones cónicas no degeneradas (proyectivas) . El teorema da una respuesta a la pregunta ¿Cuántas tangentes a un óvalo pueden pasar a través de un punto en un plano proyectivo finito? La respuesta depende esencialmente del orden (número de puntos en una línea −1) del plano.

Definición de un óvalo [ editar ]

Artículo principal: Oval (plano proyectivo).

• En un plano proyectivo un conjunto Ω de puntos se denomina ovalada , si:

1. Cualquier línea l cumple Ω en un máximo de dos puntos, y
2. Para cualquier punto P ∈ Ω existe exactamente una línea tangente t a P , es decir, t ∩ Ω = { P }.

Cuando | l ∩ Ω | = 0 la línea l es una línea exterior (o pasante ), ^[1] si | l ∩ Ω | = 1 una línea tangente y si | l ∩ Ω | = 2 la línea es una línea secante .

Para planos finitos (es decir, el conjunto de puntos es finito) tenemos una caracterización más conveniente: ^[2]

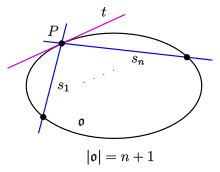
• Para un plano proyectivo finito de orden n (es decir, cualquier línea contiene n + 1 puntos) un conjunto Ω de puntos es un óvalo si y solo si | Ω | = n + 1 y no hay tres puntos colineales (en una línea común).

Declaración y prueba del teorema de Qvist [ editar ]

Teorema de Qvist ^[3] [4]

Vamos Ω ser un óvalo en un plano proyectivo finito de orden n .

(a) Si n es impar ,

cada punto P ∉ Ω es incidente con 0 o 2 tangentes.

(b) Si n es par ,

existe un punto N , el núcleo o nudo , de manera que, el conjunto de las tangentes a ovalada Ω es el lápiz de todas las líneas a través de N .

Teorema de Qvist: a la prueba en caso de n impar

Teorema de Qvist: a la prueba en caso de n incluso

Prueba

(a) Sea t _R la tangente a Ω en el punto R y sea P ₁ , ..., P _n los puntos restantes de esta línea. Para cada i , las líneas a través de la partición P _i Ω en conjuntos de cardinalidad 2 o 1 o 0. Desde el número | Ω | = n + 1 es par, para cualquier punto P _i , debe existir al menos una tangente más a través de ese punto. El número total de tangentes es n + 1 , por lo tanto, hay exactamente dos tangentes a través de cada P _i, t _R y otro. Por lo tanto, para cualquier punto P que no esté en el óvalo Ω , si P está en una tangente a Ω , está exactamente en dos tangentes.

(b) Sea s una secante, s ∩ Ω = { P ₀ , P ₁ } y s = { P ₀ , P ₁ , ..., P _n }. Porque | Ω | = n + 1 es impar, a través de cualquier P _i , i = 2, ..., n , pasa al menos una tangente t _i . El número total de tangentes es n + 1 . Por lo tanto, a través de cualquier punto P _i para i = 2, ..., n hay exactamente una tangente. SiN es el punto de intersección de dos tangentes, no secante puede pasar a través de N . Como n + 1 , el número de tangentes, es también el número de líneas a través de cualquier punto, cualquier línea a través de N es una tangente.

Ejemplo en un plano pappiano de orden par.

Usando coordenadas no homogéneas sobre un campo K , | K | = n par, el conjunto

Ω ₁ = {( x, y ) | y = x ² } ∪ {(∞) },

El cierre proyectivo de la parábola y = x ² , es un óvalo con el punto N = (0) como núcleo (ver imagen), es decir, cualquier línea y = c , con c ∈ K , es una tangente.

Definición y propiedad de hiperovales [ editar ]

• Cualquier ovalada Ω en un finito plano proyectivo de incluso orden n tiene un núcleo N .

El conjunto de puntos Ω  : = Ω ∪ { N } se denomina hiperoval o ( n + 2 ) - arco . (Un óvalo finito es un arco( n + 1 ) ).

Uno comprueba fácilmente la siguiente propiedad esencial de un hiperoval:

• Para un hiperoval Ω y un punto R ∈ Ω el conjunto de puntos Ω \ { R } es un óvalo.

Sección cónica proyectiva Ω ₁

Esta propiedad proporciona un medio simple de construir óvalos adicionales a partir de un óvalo dado.

Ejemplo

Para un plano proyectivo sobre un campo finito K , | K | = n par y n > 4 , el conjunto

Ω ₁ = {( x, y ) | y = x ² } ∪ {(∞) } es un óvalo (sección cónica) (ver imagen),

Ω ₁ = {( x, y ) | y = x ² } ∪ {(0), (∞) } es un hiperoval y

Ω ₂ = {( x, y ) | y = x ² } ∪ {(0) } es otro óvalo que no es una sección cónica. (Recuerde que una sección cónica está determinada únicamente por 5 puntos).

En geometría métrica , el teorema de encolado de Reshetnyak proporciona información sobre la estructura de un objeto geométrico utilizando como bloques de construcción otros objetos geométricos, pertenecientes a una clase bien definida . Intuitivamente, establece que una variedad obtenida al unir (es decir, " pegar ") entre sí, de una manera definida con precisión, otras variedades que tienen una propiedad determinada heredan esa misma propiedad.

El teorema fue declarado y probado por primera vez por Yurii Reshetnyak en 1968. ^[1]

Declaración [ editar ]

Teorema: vamos$${\ displaystyle X_ {i}}Ser completos localmente espacios métricos geodésicos compactos de curvatura CAT $${\ displaystyle \ leq \ kappa}y $${\ displaystyle C_ {i} \ subset X_ {i}} subconjuntos convexos que son isométricos . Entonces el colector $${\ displaystyle X}, obtenido pegando todo $${\ displaystyle X_ {i}} a lo largo de todo $${\ displaystyle C_ {i}}, también es de curvatura CAT. $${\ displaystyle \ leq \ kappa}.

Para una exposición y una prueba del Teorema de encolado de Reshetnyak, ver ( Burago, Burago & Ivanov 2001, Teorema 9.1.21).

teorema de Saccheri – Legendre establece que la suma de los ángulos en un triángulo es a lo sumo 180 °. ^[1] La geometría absoluta es la geometría obtenida al asumir todos los axiomas que conducen a la geometría euclidiana, con la excepción del axioma que es equivalente al postulado paralelo de Euclid. ^[2]

El teorema lleva el nombre de Giovanni Girolamo Saccheri y Adrien-Marie Legendre .

La existencia de al menos un triángulo con una suma de ángulo de 180 grados en geometría absoluta implica el postulado paralelo de Euclides. De manera similar, la existencia de al menos un triángulo con una suma de ángulos de menos de 180 grados implica el postulado característico de la geometría hiperbólica .

Max Dehn dio un ejemplo de una geometría no legendaria donde la suma de ángulos de un triángulo es mayor que 180 grados, y una geometría semi-euclidiana donde hay un triángulo con una suma de ángulos de 180 grados pero el postulado paralelo de Euclides falla. En las geometrías de Dehn, el axioma arquimediano no se sostiene.

a la definición de un óvalo finito: $${\ displaystyle t}tangente, $${\ displaystyle s_ {1}, ... s_ {n}} secantes $${\ displaystyle n} es el orden del plano proyectivo (número de puntos en una línea -1)

En la geometría proyectiva, el teorema de Segre , que lleva el nombre del matemático italiano Beniamino Segre , es la afirmación:

• Cualquier óvalo en un plano proyectivo pappiano finito de orden impar es una sección cónica proyectiva no degenerada .

Esta declaración fue asumida en 1949 por los dos matemáticos finlandeses G. Järnefelt y P. Kustaanheimo y su prueba fue publicada en 1955 por B. Segre.

Un plano proyectivo pappian finita puede ser imaginado como el cierre proyectiva del plano real (por una línea en el infinito), donde los números reales se sustituyen por un campo finito K . Orden impar significa que | K | = n es impar. Un óvalo es una curva similar a un círculo (vea la definición a continuación): cualquier línea lo encuentra en un máximo de 2 puntos y en cualquier punto de la misma hay exactamente una tangente. Los ejemplos estándar son las secciones cónicas proyectivas no degeneradas.

Para los planos proyectivos pappianos de orden uniforme , siempre hay óvalos que no son cónicos. En un plano infinito existen óvalos, que no son cónicos. En el plano real, uno simplemente pega la mitad de un círculo y una elipse adecuada sin problemas .

La prueba del teorema de Segre, que se muestra a continuación, utiliza la versión de 3 puntos del teorema de Pascal y una propiedad de un campo finito de orden impar, es decir, que el producto de todos los elementos distintos de cero es -1.

Definición de un óvalo [ editar ]

Artículo principal: Oval (plano proyectivo).

• En un plano proyectivo un conjunto. $${\ displaystyle {\ mathfrak {o}}}de puntos se llama ovalo , si:

(1) Cualquier línea $${\ displaystyle g} cumple $${\ displaystyle {\ mathfrak {o}}} en a lo sumo dos puntos.

Si $${\ displaystyle | g \ cap {\ mathfrak {o}} | = 0} la línea $${\ displaystyle g}es una línea exterior (o de paso ); en caso$${\ displaystyle | g \ cap {\ mathfrak {o}} | = 1}una línea tangente y si$${\ displaystyle | g \ cap {\ mathfrak {o}} | = 2}La línea es una línea secante .

(2) Para cualquier punto. $${\ displaystyle P \ in {\ mathfrak {o}}} existe exactamente una tangente $${\ displaystyle t}en P , es decir,$${\ displaystyle t \ cap {\ mathfrak {o}} = \ {P \}}.

Para planos finitos (es decir, el conjunto de puntos es finito) tenemos una caracterización más conveniente:

• Para un plano proyectivo finito de orden n (es decir, cualquier línea contiene n + 1 puntos) un conjunto$${\ displaystyle {\ mathfrak {o}}} de puntos es un ovalo si y solo si $${\ displaystyle | {\ mathfrak {o}} | = n + 1}y no hay tres puntos colineales (en una línea común).

Versión de 3 puntos de Pascal [ editar ]

para la prueba $${\ displaystyle g _ {\ infty}} es la tangente en $${\ displaystyle P_ {3}}

Teorema

Permitir $${\ displaystyle {\ mathfrak {o}}}Un óvalo en un plano proyectivo de carácter pappiano. $${\ displaystyle \ neq 2}. 
$${\ displaystyle {\ mathfrak {o}}}es una declaración cónica no degenerada si y solo si la declaración (P3) es válida:

(P3): Seamos$${\ displaystyle P_ {1}, P_ {2}, P_ {3}} cualquier triángulo en $${\ displaystyle {\ mathfrak {o}}} y $${\ displaystyle {\ overline {P_ {i} P_ {i}}}} la tangente en el punto $${\ displaystyle P_ {i}} a $${\ displaystyle {\ mathfrak {o}}}, luego los puntos

$${\ displaystyle P_ {4}: = {\ overline {P_ {1} P_ {1}}} \ cap {\ overline {P_ {2} P_ {3}}}, \ P_ {5}: = {\ overline {P_ {2} P_ {2}}} \ cap {\ overline {P_ {1} P_ {3}}}, \ P_ {6}: = {\ overline {P_ {3} P_ {3}}} \ gorra {\ línea {P_ {1} P_ {2}}}}

son colineales ^[1]

a la prueba del teorema de Pascal de 3 puntos

Prueba

Dejemos que el plano proyectivo se coordine de forma no homogénea en un campo.$${\ displaystyle K} tal que $${\ displaystyle P_ {3} = (0), \; g _ {\ infty}} es la tangente en $${\ displaystyle P_ {3}, \ (0,0) \ en {\ mathfrak {o}}}, el eje x es la tangente en el punto $${\ displaystyle (0,0)} y $${\ displaystyle {\ mathfrak {o}}} contiene el punto $${\ displaystyle (1,1)}. Además, nos propusimos$${\ displaystyle P_ {1} = (x_ {1}, y_ {1}), \; P_ {2} = (x_ {2}, y_ {2}) \.}(s. imagen) 
El óvalo$${\ displaystyle {\ mathfrak {o}}} puede ser descrito por una función $${\ displaystyle f: K \ mapsto K} tal que

$${\ displaystyle {\ mathfrak {o}} = \ {(x, y) \ en K ^ {2} \; | \; y = f (x) \} \ \ cup \ {(\ infty) \} \ ;.}

La tangente en el punto. $${\ displaystyle (x_ {0}, f (x_ {0}))} será descrito usando una función $${\ displaystyle f '} tal que su ecuación es

$${\ displaystyle y = f '(x_ {0}) (x-x_ {0}) + f (x_ {0})}

Por lo tanto (s. Imagen)

$${\ displaystyle P_ {5} = (x_ {1}, f '(x_ {2}) (x_ {1} -x_ {2}) + f (x_ {2}))} y $${\ displaystyle P_ {4} = (x_ {2}, f '(x_ {1}) (x_ {2} -x_ {1}) + f (x_ {1})) \ ;.}

Yo: si$${\ displaystyle {\ mathfrak {o}}} Es una cónica no degenerada que tenemos. $${\ displaystyle f (x) = x ^ {2}} y $${\ displaystyle f '(x) = 2x} y uno calcula fácilmente que $${\ displaystyle P_ {4}, P_ {5}, P_ {6}} son colineales

Ii: si$${\ displaystyle {\ mathfrak {o}}}Es un óvalo con propiedad (P3) , la pendiente de la línea.$${\ displaystyle {\ overline {P_ {4} P_ {5}}}} es igual a la pendiente de la recta $${\ displaystyle {\ overline {P_ {1} P_ {2}}}}, eso significa:

$${\ displaystyle f '(x_ {2}) + f' (x_ {1}) - {\ frac {f (x_ {2}) - f (x_ {1})} {x_ {2} -x_ {1 }}} = {\ frac {f (x_ {2}) - f (x_ {1})} {x_ {2} -x_ {1}}}} y por lo tanto

(yo): $${\ displaystyle (f '(x_ {2}) + f' (x_ {1})) (x_ {2} -x_ {1}) = 2 (f (x_ {2}) - f (x_ {1} ))} para todos $${\ displaystyle x_ {1}, x_ {2} \ en K}.

Con $${\ displaystyle f (0) = f '(0) = 0} uno obtiene

(ii): $${\ displaystyle f '(x_ {2}) x_ {2} = 2f (x_ {2})} y de $${\ displaystyle f (1) = 1} obtenemos

(iii): $${\ displaystyle f '(1) = 2 \ ;.}

(i) y (ii) rendimiento

(iv): $${\ displaystyle f '(x_ {2}) x_ {1} = f' (x_ {1}) x_ {2}} y con (iii) al menos obtenemos

(v): $${\ displaystyle f '(x_ {2}) = 2x_ {2}} para todos $${\ displaystyle x_ {2} \ en K}.

Una consecuencia de (ii) y (v) es

$${\ displaystyle f (x_ {2}) = x_ {2} ^ {2}, \; x_ {2} \ en K}.

Por lo tanto $${\ displaystyle {\ mathfrak {o}}} Es una cónica no degenerada.

Observación: La propiedad (P3) se cumple para cualquier óvalo en un plano proyectivo pappiano de la característica 2 con un núcleo (todas las tangentes se encuentran en el núcleo). Por lo tanto, en este caso (P3) también es cierto para óvalos no cónicos. ^[2]

El teorema de Segre y su demostración [ editar ]

Teorema

Cualquier ovalo $${\ displaystyle {\ mathfrak {o}}}en un plano proyectivo pappiano finito de orden impar hay una sección cónica no degenerada.

Versión de 3 puntos del teorema de Pascal, para la prueba que asumimos $${\ displaystyle g _ {\ infty} = {\ overline {P_ {2} P_ {3}}}}

Teorema de Segre: a su prueba.

Prueba

^[3]

Para la prueba, mostramos que el óvalo tiene propiedad (P3) de la versión de 3 puntos del teorema de Pascal.

Permitir $${\ displaystyle P_ {1}, P_ {2}, P_ {3}} cualquier triángulo en $${\ displaystyle {\ mathfrak {o}}} y $${\ displaystyle P_ {4}, P_ {5}, P_ {6}}Se define como se describe en (P3) . El plano pappiano se coordinará de forma no homogénea en un campo finito. $${\ displaystyle K}, tal que$${\ displaystyle P_ {3} = (\ infty), \; P_ {2} = (0), \; P_ {1} = (1,1)} y $${\ displaystyle (0,0)} es el punto común de las tangentes en $${\ displaystyle P_ {2}} y $${\ displaystyle P_ {3}}. El ovalo$${\ displaystyle {\ mathfrak {o}}}Se puede describir utilizando una función biyectiva .$${\ displaystyle f: K ^ {*}: = K \ cup \ setminus \ {0 \} \ mapsto K ^ {*}}:

$${\ displaystyle {\ mathfrak {o}} = \ {(x, y) \ en K ^ {2} \; | \; y = f (x), \; x \ neq 0 \} \; \ cup \ ; \ {(0), (\ infty) \} \ ;.}

Por un punto $${\ displaystyle P = (x, y), \; x \ en K \ setminus \ {0,1 \}}, la expresion $${\ displaystyle m (x) = {\ tfrac {f (x) -1} {x-1}}} es la pendiente de la secante $${\ displaystyle {\ overline {PP_ {1}}} \ ;.} Porque tanto las funciones $${\ displaystyle x \ mapsto f (x) -1} y $${\ displaystyle x \ mapsto x-1} son bijections de $${\ displaystyle K \ setminus \ {0,1 \}} a $${\ displaystyle K \ setminus \ {0, -1 \}}y $${\ displaystyle x \ mapsto m (x)} una bijección de $${\ displaystyle K \ setminus \ {0,1 \}} sobre $${\ displaystyle K \ setminus \ {0, m_ {1} \}}, dónde $${\ displaystyle m_ {1}} es la pendiente de la tangente en $${\ displaystyle P_ {1}}, para $${\ displaystyle K ^ {**}: = K \ setminus \ {0,1 \} \ ;:} obtenemos

$${\ displaystyle \ prod _ {x \ en K ^ {**}} (f (x) -1) = \ prod _ {x \ en K ^ {**}} (x-1) = 1 \ quad { \ text {und}} \ quad m_ {1} \ cdot \ prod _ {x \ en K ^ {**}} {\ frac {f (x) -1} {x-1}} = - 1 \; .}

(Comentario: Para $${\ displaystyle K ^ {*}: = K \ setminus \ {0 \}} tenemos: $${\ displaystyle \ displaystyle \ prod _ {k \ en K ^ {*}} k = -1 \ ;.}) 
Por lo tanto

$${\ displaystyle -1 = m_ {1} \ cdot \ prod _ {x \ en K ^ {**}} {\ frac {f (x) -1} {x-1}} = m_ {1} \ cdot {\ frac {\ displaystyle \ prod _ {x \ en K ^ {**}} (f (x) -1)} {\ displaystyle \ prod _ {x \ en K ^ {**}} (x-1 )}} = m_ {1} \ ;.}

Porque las pendientes de linea $${\ displaystyle {\ overline {P_ {5} P_ {6}}}} y tangente $${\ displaystyle {\ overline {P_ {1} P_ {1}}}} ambos son $${\ displaystyle -1}, resulta que $${\ displaystyle {\ overline {P_ {1} P_ {1}}} \ cap {\ overline {P_ {2} P_ {3}}} = P_ {4} \ in {\ overline {P_ {5} P_ { 6}}}}. Esto es cierto para cualquier triángulo.$${\ displaystyle P_ {1}, P_ {2}, P_ {3} \ en {\ mathfrak {o}}}.

Entonces: (P3) del teorema de Pascal de 3 puntos se mantiene y el óvalo es una cónica no degenerada.