GEOMETRÍA -TEOREMAS EN GEOMETRÍA

teorema de Petersen-Morley establece que, si a , b , c son tres líneas de sesgo generales en el espacio, si a ' , b' , c ' son las líneas de distancia más corta respectivamente para los pares (b, c) , (c, a) y (a, b) , y si p , q y r son las líneas de distancia más corta, respectivamente, para los pares (a, a ') , (b, b') y (c, c ') , entonces hay una sola línea reunida en ángulos rectos todos p , q , y r .

El teorema lleva el nombre de Julius Petersen y Frank Morley .

teorema de Petr-Douglas-Neumann (o el teorema de PDN ) es un resultado relacionado con polígonos planos arbitrarios . El teorema afirma que un cierto procedimiento cuando se aplica a un polígono arbitrario siempre produce un polígono regular que tiene el mismo número de lados que el polígono inicial. El teorema fue publicado por primera vez por Karel Petr (1868–1950) de Praga en 1908. ^[1] [2] El teorema fue redescubierto independientemente por Jesse Douglas (1897–1965) en 1940 ^[3] y también por BH Neumann(1909– 2002) en 1941.^[2] [4] La denominación del teorema como teorema de Petr-Douglas-Neumann , o como elteorema de PDN para abreviar, se debe a Stephen B Gray. ^[2] Este teorema también se ha llamado el teorema de Douglas , el teorema de Douglas-Neumann , el teorema de Napoleón-Douglas-Neumann y el teorema de Petr . ^[2]

El teorema de PDN es una generalización del teorema de Napoleón que se ocupa de los triángulos arbitrarios y del teorema de van Aubel que se relaciona con cuadriláteros arbitrarios .

Declaración del teorema [ editar ]

El teorema de Petr-Douglas-Neumann afirma lo siguiente. ^[3] [5]

Si los triángulos isósceles con ángulos de vértice 2kπ / n se erigen en los lados de un n-gon A ₀ arbitrario , y si este proceso se repite con el n-gon formado por los vértices libres de los triángulos, pero con un valor diferente de k , y así sucesivamente hasta que se hayan utilizado todos los valores 1 ≤ k ≤ n - 2 (en orden arbitrario), luego se forma un n-gon regular A _{n − 2} cuyo centroide coincide con el centroide de A ₀ .

Especialización en triángulos [ editar ]

Diagrama que ilustra el hecho de que el teorema de Napoleón es un caso especial del teorema de Petr-Douglas-Neumann.

En el caso de los triángulos, el valor de n es 3 y el de n  - 2 es 1. Por lo tanto, solo hay un valor posible para k , a saber 1. La especialización del teorema a los triángulos afirma que el triángulo A ₁ es un elemento regular. 3-gon, es decir, un triángulo equilátero.

A ₁ está formado por los vértices de los triángulos isósceles con un ángulo de ápice 2π / 3 erigido sobre los lados del triángulo A ₀ . Los vértices de A ₁ son los centros de los triángulos equiláteros erigidos sobre los lados del triángulo A ₀ . Así, la especialización del teorema de la PDN a un triángulo se puede formular de la siguiente manera:

Si los triángulos equiláteros se erigen sobre los lados de cualquier triángulo, entonces el triángulo formado por los centros de los tres triángulos equiláteros es equilátero.

La última afirmación es la afirmación del teorema de Napoleón .

Especialización a cuadriláteros [ editar ]

En el caso de cuadriláteros , el valor de n es 4 y el de n  - 2 es 2. Hay dos valores posibles para k , a saber, 1 y 2, y por lo tanto dos ángulos de vértice posibles, a saber:

(2 × 1 × π) / 4 = π / 2 = 90 ° (correspondiente a k = 1)

(2 × 2 × π) / 4 = π = 180 ° (correspondiente a k = 2).

De acuerdo con el teorema de PDN, el cuadrilátero A ₂ es un 4-gon regular, es decir, un cuadrado . El proceso de dos etapas que produce el cuadrado A ₂ se puede llevar a cabo de dos maneras diferentes. (El vértice Z de un triángulo isósceles con un ángulo de vértice π erigido sobre un segmento de línea XY es el punto medio del segmento de línea XY ).

Construya A ₁ usando el ángulo de vértice π / 2 y luego A ₂ con el ángulo de vértice π. [ editar ]

En este caso, los vértices de A ₁ son los vértices libres de los triángulos isósceles con ángulos de vértice π / 2 erigidos sobre los lados del cuadrilátero A ₀ . Los vértices del cuadrilátero A ₂ son los puntos medios de los lados del cuadrilátero A ₁ . Por el teorema de la PDN, A ₂ es un cuadrado.

Los vértices del cuadrilátero A ₁ son los centros de cuadrados erigidos sobre los lados del cuadrilátero A ₀ . La afirmación de que el cuadrilátero A ₂ es un cuadrado es equivalente a la afirmación de que las diagonales de A ₁son iguales y perpendiculares entre sí. La última afirmación es el contenido del teorema de van Aubel .

Así, el teorema de van Aubel es un caso especial del teorema de PDN.

Construya A ₁ utilizando el ángulo de vértice π y luego A ₂ con el ángulo de vértice π / 2. [ editar ]

En este caso, los vértices de A ₁ son los puntos medios de los lados del cuadrilátero A ₀ y los de A ₂ son los vértices de los triángulos con ángulos de vértice π / 2 erigidos sobre los lados de A ₁ . El teorema PDN afirma que A _{2 también} es un cuadrado en este caso.

Imágenes que ilustran la aplicación del teorema a cuadriláteros [ editar ]

El teorema de Petr – Douglas – Neumann  aplicado a un cuadrilátero A 0 = ABCD .  A 1 = EFGH se construye utilizando el  ángulo de vértice π / 2 y A 2 = PQRS con el ángulo de vértice π.	El teorema de Petr – Douglas – Neumann  aplicado a un cuadrilátero A 0 = ABCD .  A 1 = EFGH se construye utilizando el  ángulo de vértice π y A 2 = PQRS con el ángulo de vértice π / 2.

El teorema de Petr-Douglas-Neumann  aplicado a un cuadrilátero de auto-intersección A 0 =ABCD . A 1 = EFGH se construye utilizando el ángulo de vértice π / 2 y A 2 = PQRS con el ángulo de vértice π.	El teorema de Petr-Douglas-Neumann  aplicado a un cuadrilátero de auto-intersección A 0 =ABCD . A 1 = EFGH se construye utilizando el ángulo de vértice π y A 2 = PQRS con el ángulo de vértice π / 2.

Diagrama que ilustra el hecho de que el teorema de van Aubel es  un caso especial del teorema de Petr-Douglas-Neumann.

Especialización en pentágonos [ editar ]

Diagrama que ilustra el teorema de Petr-Douglas-Neumann aplicado a un pentágono. El pentágono A ₀es ABCDE . A ₁ (= FGHIJ ) se construye con un ángulo de vértice de 72 °, A ₂ (= KLMNO ) con un ángulo de vértice de 144 ° y A ₃ (= PQRST ) con un ángulo de vértice de 216 °.

En el caso de los pentágonos , tenemos n = 5 y n  - 2 = 3. Por lo tanto, hay tres valores posibles para k , a saber, 1, 2 y 3, y por lo tanto, tres ángulos de vértice posibles para los triángulos isósceles:

(2 × 1 × π) / 5 = 2π / 5 = 72 °

(2 × 2 × π) / 5 = 4π / 5 = 144 °

(2 × 3 × π) / 5 = 6π / 5 = 216 °

Según el teorema de PDN, A ₃ es un pentágono regular . El proceso de tres etapas que conduce a la construcción del pentágono regular A ₃ se puede realizar de seis maneras diferentes según el orden en que se seleccionan los ángulos de vértice para la construcción de los triángulos isósceles.

Numero de serie	Ángulo de ápice  en la construcción de A 1.	Ángulo de ápice  en la construcción de A 2.	Ángulo de ápice  en la construcción de A 3.
1	72 °	144 °	216 °
2	72 °	216 °	144 °
3	144 °	72 °	216 °
4	144 °	216 °	72 °
5	216 °	72 °	144 °
6	216 °	144 °	72 °

Demostración del teorema [ editar ]

El teorema se puede probar usando algunos conceptos elementales del álgebra lineal. ^[2] [6]

La prueba comienza con la codificación de un n -gon por una lista de números complejos que representan los vértices del n -gon. Esta lista puede ser pensado como un vector en el n -dimensional complejo espacio lineal C ⁿ. Tome un n -gon A y que sea representado por el vector complejo

A = ( a ₁ , a ₂ , ..., a _n ).

Deje que el polígono B esté formado por los vértices libres de triángulos similares construidos en los lados de A y deje que se represente por el vector complejo

B = ( b ₁ , b ₂ , ..., b _n ).

Entonces nosotros tenemos

α ( a _r - b _r ) = a _r +1 - b _r , donde α = exp ( i ) para algunos θ (aquí i es la raíz cuadrada de −1).

Esto produce la siguiente expresión para calcular las b _r 's:

b _r = (1 − α) ⁻¹ ( a _r +1 - α a _r ).

En términos del operador lineal S  : C ⁿ → C ⁿ que permuta cíclicamente las coordenadas en un lugar, tenemos

B = (1 − α) ⁻¹ ( S - α I ) A , donde I es la matriz de identidad.

Esto significa que el polígono A _n −2 que debemos mostrar es regular se obtiene de A ₀ aplicando la composición de los siguientes operadores:

(1 - ω ^k ) ⁻¹ ( S - ω ^k I ) para k = 1, 2, ..., n - 2, donde ω = exp (2π i / n ). (Estos conmutan porque son todos polinomios en el mismo operador S ).

Un polígono P = ( p ₁ , p ₂ , ..., p _n ) es un n- gon regular si cada lado de P se obtiene del siguiente girando a través de un ángulo de 2π / n , es decir, si

p _{r + 1} - p _r = ω ( p _{r + 2} - p _{r + 1} ).

Esta condición se puede formular en términos de S de la siguiente manera:

( S - I ) ( I - ω S ) P = 0.

O equivalentemente como

( S - I ) ( S - ω ^{n - 1} I ) P = 0, ya que ω ⁿ = 1.

El teorema de Petr-Douglas-Neumann ahora sigue de los siguientes cálculos.

( S - I ) ( S - ω ^{n - 1} I ) A _{n - 2}

= ( S - I ) ( S - ω ^{n - 1} I ) (1 - ω) ⁻¹ ( S - ω I ) (1 - ω ² ) ⁻¹ ( S - ω ² I ) ... (1 - ^{n - 2} ) ⁻¹ ( S - ω ^{n - 2} I ) A ₀

= (1 - ω) ⁻¹ (1 - ω ² ) ⁻¹ ... (1 - ω ^{n - 2} ) ⁻¹ ( S - I ) ( S - ω I ) ( S - ω ² I ) ... ( S - ω ^{n - 1} I ) A ₀

= (1 - ω) ⁻¹ (1 - ω ² ) ⁻¹ ... (1 - ω ^{n - 2} ) ⁻¹ ( S ⁿ - I ) A ₀

= 0, ya que S ⁿ = I .

i = 7 , b = 8 ,A = i +b/2 - 1 = 10

El triángulo con vértices en los puntos inferior izquierdo, inferior derecho y superior derecho tiene i = 12 y b = 14 , que se obtienen mediante el teorema de Pick A = i + b/2 - 1 = 18 ; esto es confirmado por el área de triángulo fórmula 1/2 × de base x altura = 1/2 × 9 × 4 = 18.

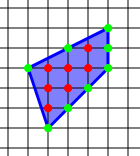
Dado un polígono simple construido en una cuadrícula de puntos con igual distancia (es decir, puntos con coordenadas enteras ) de manera que todos los vértices del polígono son puntos de cuadrícula, el teorema de Pick proporciona una fórmulasimple para calcular el área A de este polígono en términos del número i de puntosde celosía en el interior ubicado en el polígono y el número b de puntos de celosía en el límite colocado en el perímetro del polígono: ^[1]

$${\ displaystyle A = i + {\ frac {b} {2}} - 1.}

En el ejemplo mostrado, tenemos i = 7 puntos interiores y b = 8 puntos de los límites, por lo que la zona es A  = 7 +  8/2  - 1 = 7 + 4 - 1 = 10 unidades cuadradas.

Tenga en cuenta que el teorema como se indicó anteriormente solo es válido para polígonos simples , es decir, aquellos que constan de una sola pieza y no contienen agujeros. Para un polígono que tiene agujeros de h , con un límite en forma de h + 1 curvas cerradas simples, la fórmula i + b/2 + h - 1 un poco más complicada da el área.

El resultado fue descrito por primera vez por Georg Alexander Pick en 1899. ^[2] El tetraedro de Reeve muestra que no hay un análogo del teorema de Pick en tres dimensiones que exprese el volumen de un politopo al contar sus puntos interiores y de contorno. Sin embargo, hay una generalización en dimensiones más altas a través de los polinomios de Ehrhart . La fórmula también generaliza a superficies de poliedros .

Prueba [ editar ]

Considere un polígono P y un triángulo T , con un borde en común con P . Supongamos que el teorema de Pick es verdadero para P y T por separado; queremos mostrar que también es cierto para el polígono PT obtenida por adición de T a P . Como P y T comparten un borde, todos los puntos de límite a lo largo del borde en común se fusionan con los puntos interiores, a excepción de los dos puntos finales del borde, que se fusionan con los puntos de límite. Entonces, al llamar el número de puntos de límite en c común , tenemos ^[3]

$${\ displaystyle i_ {PT} = i_ {P} + i_ {T} + (c-2)}

y

$${\ displaystyle b_ {PT} = b_ {P} + b_ {T} -2 (c-2) -2.}

De lo que sigue sigue

$${\ displaystyle i_ {P} + i_ {T} = i_ {PT} - (c-2)}

y

$${\ displaystyle b_ {P} + b_ {T} = b_ {PT} +2 (c-2) +2.}

Dado que estamos asumiendo el teorema para P y para T por separado,

{\ displaystyle {\ begin {alineado} A_ {PT} & = A_ {P} + A_ {T} \\ & = \ left (i_ {P} + {\ frac {b_ {P}} {2}} - 1 \ derecha) + \ izquierda (i_ {T} + {\ frac {b_ {T}} {2}} - 1 \ derecha) \\ & = i_ {P} + i_ {T} + {\ frac {b_ {P} + b_ {T}} {2}} - 2 \\ & = i_ {PT} - (c-2) + {\ frac {b_ {PT} +2 (c-2) +2} {2 }} - 2 \\ & = i_ {PT} + {\ frac {b_ {PT}} {2}} - 1. \ end {alineado}}}

Por lo tanto, si el teorema es verdadero para los polígonos construidos a partir de n triángulos, el teorema también es válido para los polígonos construidos a partir de n + 1 triángulos. Para los politopos generales , es bien sabido que siempre se pueden triangular . Que esto sea cierto en la dimensión 2 es un hecho fácil. Para terminar la prueba por inducción matemática , queda por demostrar que el teorema es verdadero para los triángulos. La verificación para este caso se puede hacer en estos pasos cortos:

• observe que la fórmula es válida para cualquier unidad cuadrada (con vértices que tienen coordenadas enteras);
• deduzca de esto que la fórmula es correcta para cualquier rectángulo con lados paralelos a los ejes;
• dedúzcalo, ahora, para los triángulos rectángulos obtenidos al cortar dichos rectángulos a lo largo de una diagonal ;
• ahora cualquier triángulo se puede convertir en un rectángulo uniendo tales triángulos rectos; ya que la fórmula es correcta para los triángulos rectos y para el rectángulo, también se aplica para el triángulo original.

El último paso utiliza el hecho de que si el teorema es verdadero para el polígono PT y para el triángulo T , entonces también es cierto para P ; Esto se puede ver mediante un cálculo muy similar al que se muestra arriba.