GEOMETRÍA - TEOREMAS EN GEOMETRÍA

El teorema aplicado a un cilindro abierto, cono y una esfera para obtener sus áreas de superficie. Los centroides están a una distancia a(en rojo) del eje de rotación.

En matemáticas, el teorema del centroide de Pappus (también conocido como el teorema de Guldinus , el teorema de Pappus-Guldinus o el teorema de Pappus) es uno de los dos teoremas relacionados que tratan las áreas de la superficie y los volúmenes de superficies y sólidos de la revolución.

Los teoremas se atribuyen a Pappus de Alejandría ^[a] y Paul Guldin .

El primer teorema [ editar ]

El primer teorema establece que el área de superficie A de una superficie de revolución generada al girar una curva plana C alrededor de un eje externo a C y en el mismo plano es igual al producto de la longitud del arco sde C y la distancia d recorrida por El centroide geométrico de C :

$${\ displaystyle A = sd.}

Por ejemplo, el área de superficie del toro con radio menor r y radio mayor R es

$${\ displaystyle A = (2 \ pi r) (2 \ pi R) = 4 \ pi ^ {2} Rr.}

El segundo teorema [ editar ]

El segundo teorema afirma que el volumen V de un sólido de revolución generado por la rotación de una figura plana F alrededor de un eje externo es igual al producto de la zona A de F y la distancia d recorrida por el centroide geométrico de F . (Tenga en cuenta que el centroide de F suele ser diferente del centroide de su curva de límite C ). Eso es:

$${\ displaystyle V = Ad.}

Por ejemplo, el volumen del toro con radio menor r y radio mayor R es

$${\ displaystyle V = (\ pi r ^ {2}) (2 \ pi R) = 2 \ pi ^ {2} Rr ^ {2}.}

Este caso especial fue derivado por Johannes Kepler utilizando infinitesimales. ^[do]

Prueba [ editar ]

Dejar $${\ displaystyle A} ser el area de $${\ displaystyle F}, $${\ displaystyle W} el sólido de la revolución de $${\ displaystyle F}y $${\ displaystyle V} el volumen de $${\ displaystyle W}. Suponer$${\ displaystyle F} comienza en el $${\ displaystyle xz}- Plano y gira alrededor de la $${\ displaystyle z}-eje. La distancia del centroide de$${\ displaystyle F} desde el $${\ displaystyle z}-axis es su $${\ displaystyle x}-coordinar

$${\ displaystyle R = {\ frac {\ iint _ {F} x \, dA} {A}},}

y el teorema establece que

$${\ displaystyle V = Ad = A \ cdot 2 \ pi R = 2 \ pi \ iint _ {F} x \, dA.}

Para mostrar esto, vamos $${\ displaystyle F}estar en el plano xz , parametrizado por$${\ displaystyle \ mathbf {\ Phi} (u, v) = (x (u, v), 0, z (u, v))} para $${\ displaystyle (u, v) \ en F ^ {*}}, una región de parámetros. Ya que$${\ displaystyle \ mathbf {\ Phi}} es esencialmente un mapeo de $${\ displaystyle \ mathbb {R} ^ {2}} a $${\ displaystyle \ mathbb {R} ^ {2}}, El área de $${\ displaystyle F}Está dada por la fórmula de cambio de variables :

$${\ displaystyle A = \ iint _ {F} dA = \ iint _ {F ^ {*}} \ left | {\ frac {\ partial (x, z)} {\ partial (u, v)}} \ right | \, du \, dv = \ iint _ {F ^ {*}} \ left | {\ frac {\ partial x} {\ partial u}} {\ frac {\ partial z} {\ partial v}} - {\ frac {\ parcial x} {\ parcial v}} {\ frac {\ parcial z} {\ parcial u}} \ derecho | \, du \, dv,}

dónde $${\ displaystyle {\ tfrac {\ partial (x, z)} {\ partial (u, v)}}}Es el determinante de la matriz jacobiana del cambio de variables.

El solido $${\ displaystyle W}tiene la parametrización toroidal$${\ displaystyle \ mathbf {\ Phi} (u, v, \ theta) = (x (u, v) \ cos \ theta, x (u, v) \ sin \ theta, z (u, v))} para $${\ displaystyle (u, v, \ theta)}en la región del parámetro $${\ displaystyle W ^ {*} = F ^ {*} \ times [0,2 \ pi]}; y su volumen es

$${\ displaystyle V = \ iiint _ {W} dV = \ iiint _ {W ^ {*}} \ left | {\ frac {\ partial (x, y, z)} {\ partial (u, v, \ theta )}} \ right | \, du \, dv \, d \ theta.}

En expansión,

{\ displaystyle {\ begin {alineado} \ left | {\ frac {\ partial (x, y, z)} {\ partial (u, v, \ theta)}} \ right | & = \ left | \ det { \ begin {bmatrix} {\ frac {\ partial x} {\ partial u}} \ cos \ theta & {\ frac {\ partial x} {\ partial v}} \ cos \ theta & -x \ sin \ theta \ \ [6pt] {\ frac {\ partial x} {\ partial u}} \ sin \ theta & {\ frac {\ partial x} {\ partial v}} \ sin \ theta & x \ cos \ theta \\ [6pt ] {\ frac {\ partial z} {\ partial u}} & {\ frac {\ partial z} {\ partial v}} & 0 \ end {bmatrix}} \ right | \\ [5pt] & = \ left | - {\ frac {\ parcial z} {\ parcial v}} {\ frac {\ parcial x} {\ parcial u}} \, x + {\ frac {\ parcial z} {\ parcial u}} {\ frac { \ partial x} {\ partial v}} \, x \ right | = \ \ left | -x \, {\ frac {\ partial (x, z)} {\ partial (u, v)}} \ right | = x \ left | {\ frac {\ partial (x, z)} {\ partial (u, v)}} \ right |. \ end {alineado}}}

La última igualdad se mantiene porque el eje de rotación debe ser externo a $${\ displaystyle F}, sentido $${\ displaystyle x \ geq 0}. Ahora,

{\ displaystyle {\ begin {alineado} V & = \ iiint _ {W ^ {*}} \ left | {\ frac {\ partial (x, y, z)} {\ partial (u, v, \ theta)} } \ right | \, du \, dv \, d \ theta = \ int _ {0} ^ {2 \ pi} \! \! \! \! \ iint _ {F ^ {*}} x (u, v) \ left | {\ frac {\ partial (x, z)} {\ partial (u, v)}} \ right | \, du \, dv \, d \ theta \\ [6pt] & = 2 \ pi \ iint _ {F ^ {*}} x (u, v) \ left | {\ frac {\ partial (x, z)} {\ partial (u, v)}} \ right | \, du \, dv = 2 \ pi \ iint _ {F} x \, dA \ end {alineado}}}

Por cambio de variables.

Generalizaciones [ editar ]

Los teoremas pueden generalizarse para curvas y formas arbitrarias, bajo condiciones apropiadas.

Goodman y Goodman ^[5] generalizan el segundo teorema de la siguiente manera. Si la cifra F se mueve a través del espacio de manera que permanece perpendicular a la curva L trazada por el centro de gravedad de F , entonces se barre un sólido de volumen V = Ad , donde A es el área de F y d es la longitud de L . (Esto supone que el sólido no se interseca por sí mismo). En particular, F puede girar alrededor de su centroide durante el movimiento.

Sin embargo, la generalización correspondiente de la primera teorema sólo es cierto si la curva L trazada por el centro de gravedad se encuentra en un plano perpendicular al plano de C .

Teorema del hexágono de Pappus: los puntos X , Y y Z están alineados en la línea de Pappus. El hexágono es AbCaBc .

En matemáticas, el teorema del hexágono de Pappus (atribuido a Pappus de Alejandría ) establece que dado un conjunto de puntos colineales A , B , C y otro conjunto de puntos colineales a , b , c , luego los puntos de intersección X , Y , Z de la línea los pares Ab y aB , Ac y aC , Bc y bC son colineales , tendidos en la línea de Pappus. Estos tres puntos son los puntos de intersección de los lados "opuestos" del hexágono AbCaBc . Se mantiene en un plano proyectivo sobre cualquier campo, pero falla para planos proyectivos sobre cualquier anillo de división no conmutativa . ^[1] Los planos proyectivos en los que el "teorema" es válido se denominan planos pappianos .

El dual de este teorema de incidencia establece que dado un conjunto de líneas concurrentes A , B , C y otro conjunto de líneas concurrentes a , b, c , luego las líneas x , y , z definidas por pares de puntos resultantes de pares de intersecciones A ∩ b y a  ∩  B , A  ∩  c y a  ∩  C , B  ∩  c y b ∩  C son concurrentes. ( Concurrente significa que las líneas pasan a través de un punto).

El teorema de Pappus es un caso especial del teorema de Pascal para una cónica, el caso límite cuando la cónica se degenera en 2 líneas rectas. El teorema de Pascal es a su vez un caso especial del teorema de Cayley-Bacharach .

La configuración de Pappus es la configuración de 9 líneas y 9 puntos que se produce en el teorema de Pappus, con cada línea reuniendo 3 de los puntos y cada punto reuniendo 3 líneas. En general, la línea Pappus no pasa por el punto de intersección de ABC y abc . ^[2] Esta configuración es auto dual . Dado que, en particular, las líneas Bc , bC , XY tienen las propiedades de las líneas x , y , z del teorema dual, y la colinealidad de X , Y , Zes equivalente a la concurrencia de Bc , bC , XY , el teorema dual es, por lo tanto, igual al teorema mismo. El gráfico Levi de la configuración de Pappus es el gráfico Pappus , un gráfico bipartito de distancia regular con 18 vértices y 27 bordes.

Prueba [ editar ]

Elija coordenadas proyectivas con

C = (1, 0, 0) , c = (0, 1, 0) , X = (0, 0, 1) , A = (1, 1, 1) .

En las líneas AC , Ac , AX , dadas por x ₂ = x ₃ , x ₁ = x ₃ , x ₂ = x ₁ , toma los puntos B , Y , b para que sean

B = ( p , 1, 1) , Y = (1, q , 1) , b = (1, 1, r )

para algunos p , q , r . Las tres líneas XB , CY , cb son x ₁ = x ₂ p , x ₂ = x ₃ q , x ₃ = x ₁ r , por lo que pasan por el mismo punto a si y solo si rqp = 1 . La condición para las tres líneas Cb , cB y XY x ₂ = x ₁ q, x ₁ = x ₃ p , x ₃ = x ₂ r para pasar por el mismo punto Z es rpq = 1 . Entonces, este último conjunto de tres líneas es concurrente si los otros ocho conjuntos son porque la multiplicación es conmutativa, entonces pq = qp . Equivalentemente, X , Y , Z son colineales.

La prueba anterior también muestra que para que el teorema de Pappus se mantenga para un espacio proyectivo sobre un anillo de división es suficiente y necesario que el anillo de división sea un campo (conmutativo). El matemático alemán Gerhard Hessenberg demostró que el teorema de Pappus implica el teorema de Desargues . ^[3] [4] En general, el teorema de Pappus se mantiene para algún plano proyectivo si y solo si es un plano proyectivo sobre un campo conmutativo. Los aviones descriptivos en los que el teorema de Pappus no posee son Desarguesian aviones descriptivos más anillos de división no conmutativos, y planos no Desarguesian .

La prueba no es válida si C , c , X resultan ser colineales. En ese caso, se puede proporcionar una prueba alternativa, por ejemplo, utilizando una referencia proyectiva diferente.

Orígenes [ editar ]

En su forma más antigua conocida, el Teorema de Pappus es las Propuestas 138, 139, 141 y 143 del Libro VII de la Colección de Pappus . ^[5] Estos son Lemmas XII, XIII, XV, XVII y en la parte del libro VII consiste en lemas para el primero de los tres libros de Euclides 's Porismas.

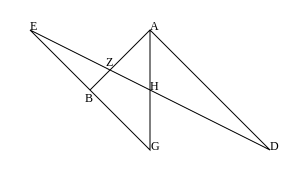
Los lemas se prueban en términos de lo que hoy se conoce como la relación cruzada de cuatro puntos colineales. Se utilizan tres lemmas anteriores. El primero de ellos, el Lema III, tiene el siguiente diagrama (que usa las letras de Pappus, con G para Γ, D para Δ, J para Θ y L para Λ).

Aquí, tres líneas rectas concurrentes, AB, AG y AD, se cruzan con dos líneas, JB y JE, que concuerdan en J. También KL se dibuja paralela a AZ. Entonces

KJ: JL :: (KJ: AG & AG: JL) :: (JD: GD & BG: JB).

Estas proporciones podrían escribirse hoy como ecuaciones: ^[6]

KJ / JL = (KJ / AG) (AG / JL) = (JD / GD) (BG / JB).

La última relación compuesta (a saber, JD: GD y BG: JB) es lo que hoy se conoce como la relación cruzada de los puntos colineales J, G, D y B en ese orden; se denota hoy por (J, G; D, B). Así que hemos demostrado que esto es independiente de la elección de la línea recta particular JD que cruza las tres líneas rectas que concurren en A. En particular

(J, G; D, B) = (J, Z; H, E).

No importa de qué lado de A caiga la línea recta JE. En particular, la situación puede ser como en el siguiente diagrama, que es el diagrama para Lemma X.

Al igual que antes, tenemos (J, G; D, B) = (J, Z; H, E). Pappus no prueba explícitamente esto; pero el Lema X es inverso, es decir, si estas dos relaciones cruzadas son las mismas, y las líneas rectas BE y DH se cruzan en A, entonces los puntos G, A y Z deben ser colineales.

Lo que mostramos originalmente se puede escribir como (J, ∞; K, L) = (J, G; D, B), con ∞ tomando el lugar de la intersección (inexistente) de JK y AG. Pappus muestra esto, en efecto, en Lemma XI, cuyo diagrama, sin embargo, tiene diferentes letras:

Lo que muestra Pappus es DE.ZH: EZ.HD :: GB: BE, que podemos escribir como

(D, Z; E, H) = (∞, B; E, G).

El diagrama para Lemma XII es:

El diagrama para el Lema XIII es el mismo, pero BA y DG, extendidos, se encuentran en N. En cualquier caso, considerando las líneas rectas a través de G como las cortadas por las tres líneas rectas a través de A (y aceptando que las ecuaciones de relaciones cruzadas siguen siendo válidas después de permutación de las entradas,) tenemos por Lemma III o XI

(G, J; E, H) = (G, D; Z).

Teniendo en cuenta las líneas rectas a través de D, cortadas por las tres líneas rectas a través de B, tenemos

(L, D; E, K) = (G, D; Z).

Por lo tanto (E, H; J, G) = (E, K; D, L), así por el lema X, los puntos H, M y K son colineales. Es decir, los puntos de intersección de los pares de lados opuestos del hexágono ADEGBZ son colineales.

Los lemas XV y XVII son que, si el punto M se determina como la intersección de HK y BG, entonces los puntos A, M y D son colineales. Es decir, los puntos de intersección de los pares de lados opuestos del hexágono BEKHZG son colineales.

Otras afirmaciones del teorema [ editar ]

Triángulos Xcc y BbY son perspectiva desde A y una , y así, también de Z .

Además de las caracterizaciones anteriores del teorema de Pappus y su dual, las siguientes son declaraciones equivalentes:

• Si los seis vértices de un hexágono se encuentran alternativamente en dos líneas, entonces los tres puntos de intersección de pares de lados opuestos son colineales. ^[7]
• Organizadas en una matriz de nueve puntos (como en la figura y la descripción anteriores) y pensadas como una evaluación permanente , si las dos primeras filas y las seis tríadas "diagonales" son colineales, entonces la tercera fila es colineal.

{\ displaystyle \ left | {\ begin {matrix} A & B & C \\ a & b & c \\ X & Y & Z \ end {matrix}} \ right |}

Es decir, si ABC , abc , ratiopharm , BCX , Cay , XBC , YCA , Zab son líneas, entonces el teorema de Pappus establece que XYZ debe ser una línea. Además, tenga en cuenta que la misma formulación matricial se aplica a la forma dual del teorema cuando ( A , B , C ), etc. son triples de líneas concurrentes. ^[8]

• Dados tres puntos distintos en cada una de las dos líneas distintas, empareje cada punto en una de las líneas con uno de la otra línea, luego las uniones de puntos no emparejados se encontrarán en pares (opuestos) en los puntos a lo largo de una línea. ^[9]
• Si dos triángulos son perspectiva en al menos dos formas diferentes, entonces son perspectiva en tres formas. ^[3]
• Si AB , CD y EF son concurrentes y DE , FA y BC son concurrentes, entonces AD , BE y CF son concurrentes.