GEOMETRÍA - TEOREMAS EN GEOMETRÍA

El teorema de Bernstein-Kushnirenko (también conocido como teorema de BKK o teorema de Bernstein-Khovanskii-Kushnirenko ^[1] ), probado por David Bernstein ^[2] y Anatoli Kushnirenko  [ ru ] ^[3] en 1975, es un teorema en álgebra . Afirma que el número de soluciones complejas no nulas de un sistema de ecuaciones polinomiales de Laurent$${\ displaystyle f_ {1} = 0, \ ldots, f_ {n} = 0}es igual al volumen mixto de los politopos de Newton de los polinomios$${\ displaystyle f_ {1}, \ ldots, f_ {n}}, asumiendo que todos los coeficientes no nulos de $${\ displaystyle f_ {n}}son genéricos Una declaración más precisa es la siguiente:

Teorema comunicado [ editar ]

Dejar $${\ displaystyle A} ser un subconjunto finito de $${\ displaystyle \ mathbb {Z} ^ {n}}. Considera el subespacio$${\ displaystyle L_ {A}} del álgebra polinomial de Laurent $${\ displaystyle \ mathbb {C} [x_ {1} ^ {\ pm 1}, \ ldots, x_ {n} ^ {\ pm 1}]}que consiste en polinomios de Laurent cuyos exponentes están en$${\ displaystyle A}. Es decir:

$${\ displaystyle L_ {A} = \ {f \ mid f (x) = \ sum _ {\ alpha \ en A} c _ {\ alpha} x ^ {\ alpha} \},}

dónde $${\ displaystyle c _ {\ alpha} \ in \ mathbb {C}} y para cada $${\ displaystyle \ alpha = (a_ {1}, \ ldots, a_ {n}) \ in \ mathbb {Z} ^ {n}} hemos utilizado la notación taquigráfica $${\ displaystyle x ^ {\ alpha}} escribir el monomio $${\ displaystyle x_ {1} ^ {a_ {1}} \ cdots x_ {n} ^ {a_ {n}}}.

Ahora toma $${\ displaystyle n} subconjuntos finitos $${\ displaystyle A_ {1}, \ ldots, A_ {n}} Con los subespacios correspondientes de los polinomios de Laurent. $${\ displaystyle L_ {A_ {1}}, \ ldots, L_ {A_ {n}}}. Considere un sistema genérico de ecuaciones de estos subespacios, que es:

$${\ displaystyle f_ {1} (x) = \ ldots = f_ {n} (x) = 0,}

donde cada $${\ displaystyle f_ {i}} es un elemento genérico en el (espacio vectorial finito dimensional) $${\ displaystyle L_ {A_ {i}}}.

El teorema de Bernstein-Kushnirenko establece que el número de soluciones $${\ displaystyle x \ in (\ mathbb {C} \ setminus 0) ^ {n}} de tal sistema es igual a

$${\ displaystyle n! \, V (\ Delta _ {1}, \ ldots, \ Delta _ {n})},

dónde $${\ displaystyle V}Denota el volumen mixto de Minkowski y para cada$${\ displaystyle i}, $${\ displaystyle \ Delta _ {i}}Es el casco convexo del conjunto finito de puntos.$${\ displaystyle A_ {i}}. Claramente$${\ displaystyle \ Delta _ {i}}Es un politopo de celosía convexo . Puede interpretarse como el politopo de Newtonde un elemento genérico del subespacio.$${\ displaystyle L_ {A_ {i}}}.

En particular, si todos los conjuntos $${\ displaystyle A_ {i}} son lo mismo $${\ displaystyle A = A_ {1} = \ cdots = A_ {n}}, entonces el número de soluciones de un sistema genérico de polinomios de Laurent de $${\ displaystyle L_ {A}} es igual a

$${\ displaystyle n! \, {\ rm {vol}} (\ Delta),}

dónde $${\ displaystyle \ Delta} es el casco convexo de $${\ displaystyle A} y vol es el usual $${\ displaystyle n}Volumen euclidiano tridimensional. Tenga en cuenta que aunque el volumen de un politopo de celosía no es necesariamente un número entero, se convierte en un número entero después de multiplicarse por$${\ displaystyle n!}.

Trivia [ editar ]

El nombre de Kushnirenko también se deletrea Kouchnirenko. David Bernstein es un hermano de Joseph Bernstein . Askold Khovanskii ha encontrado aproximadamente 15 pruebas diferentes de este teorema.

$${\ displaystyle {\ overline {BD}} \ perp {\ overline {AC}}, {\ overline {EF}} \ perp {\ overline {BC}}} $${\ displaystyle \ Rightarrow | {\ overline {AF}} | = | {\ overline {FD}} |}

En geometría , el teorema de Brahmagupta establece que si un cuadrilátero cíclico es ortodiagonal (es decir, tiene diagonales perpendiculares ), entonces la perpendicular a un lado desde el punto de intersección de las diagonales siempre biseca el lado opuesto. ^[1] Lleva el nombre del matemático indio Brahmagupta . ^[2]

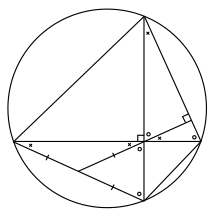
Más específicamente, sea A , B , C y D cuatro puntos en un círculo, de modo que las líneas AC y BD sean perpendiculares. Denotar la intersección de AC y BD por M . La caída de la perpendicular desde M a la línea AC , llamando a la intersección E . Sea F la intersección de la línea EM y el borde AD . Entonces, el teorema establece que F es el punto medio AD .

Prueba [ editar ]

Prueba del teorema.

Necesitamos probar que AF = FD . Probaremos que tanto AF como FDson en realidad iguales a FM .

Para probar que AF = FM , primero note que los ángulos FAM y CBM son iguales, porque son ángulos inscritos que interceptan el mismo arco del círculo. Además, los ángulos CBM y CME son ambos complementariosal ángulo BCM (es decir, suman 90 °) y, por lo tanto, son iguales. Finalmente, los ángulos CME y FMA son los mismos. Por lo tanto, AFMes un triángulo isósceles , y por lo tanto los lados AF y FM son iguales.

La prueba de que FD = FM es similar: los ángulos FDM , BCM , BME y DMF son todos iguales, por lo que DFM es un triángulo isósceles, por lo tanto, FD = FM . De ello se deduce que AF = FD , como afirma el teorema.

Caso elíptico

Caso hiperbólico

En geometría , el teorema de Braikenridge-Maclaurin , llamado así por los matemáticos británicos del siglo XVIII William Braikenridge y Colin Maclaurin , ^[1] es lo contrario al teorema de Pascal . Establece que si los tres puntos de intersección de los tres pares de líneas a través de los lados opuestos de un hexágono se encuentran en la línea L , entonces los seis vértices del hexágono se encuentran en una C cónica ; La cónica puede estar degenerada, como en el teorema de Pappus. ^[2]

El teorema de Braikenridge-Maclaurin se puede aplicar en la construcción de Braikenridge-Maclaurin , que es una construcción sintética de la cónica definida por cinco puntos, variando el sexto punto. A saber, el teorema de Pascal establece que dados seis puntos en una cónica (los vértices de un hexágono), las líneas definidas por lados opuestos se intersecan en tres puntos colineales. Esto se puede revertir para construir las ubicaciones posibles para un sexto punto, dados cinco existentes.

Teorema de la mariposa

El teorema de la mariposa es un resultado clásico en geometría euclidiana , que se puede afirmar de la siguiente manera: ^{[1] : p. 78}

Sea M el punto medio de un acorde PQ de un círculo , a través del cual se dibujan otros dos acordes AB y CD ; AD y BC intersectan el acorde PQ en X e Y correspondientemente. Entonces M es el punto medio de XY .

Prueba [ editar ]

Prueba de teorema de mariposa

Una prueba formal del teorema es la siguiente: Deje que las perpendiculares XX ′ y XX ″ se caigan del punto X en las líneas rectas AM y DM respectivamente. De manera similar, deje que YY ′ y YY ″ se caigan desde el punto Y perpendicular a las líneas rectas BM y CMrespectivamente.

Ahora desde

$${\ displaystyle \ triangle MXX '\ sim \ triangle MYY',}

$${\ displaystyle {MX \ over MY} = {XX '\ over YY'},}

$${\ displaystyle \ triangle MXX '' \ sim \ triangle MYY '',}

$${\ displaystyle {MX \ over MY} = {XX '' \ over YY ''},}

$${\ displaystyle \ triangle AXX '\ sim \ triangle CYY' ',}

$${\ displaystyle {XX '\ over YY' '} = {AX \ over CY},}

$${\ displaystyle \ triangle DXX '' \ sim \ triangle BYY ',}

$${\ displaystyle {XX '' \ over YY '} = {DX \ over BY},}

De las ecuaciones anteriores y el teorema de los acordes de intersección , se puede ver fácilmente que

$${\ displaystyle \ left ({MX \ over MY} \ right) ^ {2} = {XX '\ over YY'} {XX '' \ over YY ''},}

$${\ displaystyle {} = {AX \ cdot DX \ over CY \ cdot BY},}

$${\ displaystyle {} = {PX \ cdot QX \ over PY \ cdot QY},}

$${\ displaystyle {} = {(PM-XM) \ cdot (MQ + XM) \ over (PM + MY) \ cdot (QM-MY)},}

$${\ displaystyle {} = {(PM) ^ {2} - (MX) ^ {2} \ sobre (PM) ^ {2} - (MY) ^ {2}},}

desde PM = MQ .

Ahora,

$${\ displaystyle {(MX) ^ {2} \ over (MY) ^ {2}} = {(PM) ^ {2} - (MX) ^ {2} \ over (PM) ^ {2} - (MY ) ^ {2}}.}

Por lo tanto, se puede concluir que MX = MY , o M es el punto medio de XY .

Existen otras pruebas, ^[2] incluida una que usa geometría proyectiva. ^[3]

Historia [ editar ]

Probar el teorema de la mariposa fue planteado como un problema por William Wallace en The Gentlemen's Mathematical Companion (1803). Tres soluciones se publicaron en 1804, y en 1805 Sir William Herschel volvió a plantear la cuestión en una carta a Wallace. El Reverendo Thomas Scurr volvió a hacer la misma pregunta en 1814 en el Diario de los Caballeros o en el Repositorio Matemático .