GEOMETRÍA - TEOREMAS EN GEOMETRÍA

teorema de Mohr-Mascheroni establece que cualquier construcción geométrica que pueda ser realizada por una brújula y una regla puede ser realizada solo por una brújula.

Debe entenderse que por "cualquier construcción geométrica", nos referimos a figuras que no contienen líneas rectas, ya que es claramente imposible dibujar una línea recta sin una regla. Se entiende que una línea se determina siempre que se den o se construyan dos puntos distintos en esa línea, aunque no haya una representación visual de la línea. El teorema se puede afirmar más precisamente como: ^[1]

Cualquier construcción euclidiana, en la medida en que los elementos dados y requeridos sean puntos, se puede completar solo con la brújula si se puede completar con la brújula y la regla juntas.

Aunque el uso de una regla puede hacer que una construcción sea mucho más fácil, el teorema muestra que cualquier conjunto de puntos que define completamente una figura construida se puede determinar solo con una brújula, y la única razón para usar una regla es la estética de ver líneas rectas , que a efectos de construcción es funcionalmente innecesario.

Historia [ editar ]

El resultado fue publicado originalmente por Georg Mohr en 1672, ^[2] pero su prueba languideció en la oscuridad hasta 1928. ^{[3] [4] [5]} El teorema fue descubierto independientemente por Lorenzo Mascheroni en 1797 y fue conocido como el teorema de Mascheroni hasta El trabajo de Mohr fue redescubierto. ^[6]

Motivado por el resultado de Mascheroni, en 1822 Jean Victor Poncelet conjeturó una variación sobre el mismo tema. Propuso que cualquier construcción posible mediante regla y compás se podría hacer solo con regla. Sin embargo, la única condición es que debe proporcionarse un solo círculo con su centro identificado. El teorema de Poncelet-Steiner fue probado por Jakob Steiner once años después.

Enfoque demostración constructiva [ editar ]

Para probar el teorema, cada una de las construcciones básicas de la brújula y la regla necesita ser probada para ser posible utilizando una brújula sola, ya que estos son los cimientos de, o pasos elementales para, todas las otras construcciones. Estos son:

1. Creando la línea a través de dos puntos existentes.
2. Creando el círculo a través de un punto con centro otro punto
3. Creando el punto que es la intersección de dos líneas no paralelas existentes
4. Creación de uno o dos puntos en la intersección de una línea y un círculo (si se intersecan)
5. Creando uno o dos puntos en la intersección de dos círculos (si se intersecan).

# 1 - Una línea a través de dos puntos.

Se entiende que una línea recta no se puede trazar sin una regla. Se considera que una línea está dada por dos puntos cualquiera, ya que dos puntos cualquiera definen una línea de manera única, y una línea única se puede definir por dos puntos cualquiera en ella.

# 2 - Un círculo a través de un punto con centro definido

Esto se puede hacer con la brújula solo muy naturalmente. No hay nada que demostrar.

# 5 - Intersección de dos círculos.

Esta construcción se puede hacer directamente con una brújula siempre que se conozcan los centros y los radios de los dos círculos. Debido a la construcción de la brújula del centro de un círculo (que se muestra a continuación), siempre se puede suponer que cualquier círculo se describe por su centro y radio. De hecho, algunos autores incluyen esto en sus descripciones de las construcciones básicas. ^{[7] [8] [9]}

# 3, # 4 - Las otras construcciones

Por lo tanto, para probar el teorema, solo se deben dar construcciones de brújula para los números 3 y 4.

Pruebas alternativas [ editar ]

Se conocen varias pruebas del resultado. La prueba de Mascheroni de 1797 se basó generalmente en la idea de usar la reflexión en una línea como la herramienta principal. La solución de Mohr era diferente. ^[3] En 1890, August Adler publicó una prueba utilizando la transformación de inversión . ^[10]

Un enfoque algebraico utiliza el isomorfismo entre el plano euclidiano y el espacio de coordenadas real $${\ displaystyle \ mathbb {R} ^ {2}}. Este enfoque se puede utilizar para proporcionar una versión más sólida del teorema. ^[11] También muestra la dependencia del teorema sobre el axioma de Arquímedes (que no se puede formular en un lenguaje de primer orden ).

Prueba constructiva [ editar ]

La siguiente notación se utilizará a lo largo de este artículo. Un círculo cuyo centro está ubicado en el punto U y que pasa por el punto V se indicará por U ( V ) . Un círculo con el centro U y el radio especificado por un número, r , o un segmento de línea AB se indicará por U ( r ) o U ( AB ) , respectivamente. ^[12]

En las construcciones generales a menudo hay varias variaciones que producirán el mismo resultado. Las elecciones hechas en tal variante se pueden hacer sin pérdida de generalidad. Sin embargo, cuando se utiliza una construcción para probar que se puede hacer algo, no es necesario describir todas estas opciones y, para mayor claridad de la exposición, solo se dará una variante a continuación. Sin embargo, muchas construcciones vienen en diferentes formas dependiendo de si usan o no inversión de círculo y estas alternativas se darán si es posible.

Algunas construcciones preliminares [ editar ]

Para probar las construcciones anteriores nº 3 y nº 4, que se incluyen a continuación, a continuación se explican algunas construcciones intermedias necesarias, ya que se utilizan y se mencionan con frecuencia. Estas también son construcciones de brújula. Todas las construcciones a continuación se basan en # 1, # 2, # 5, y en cualquier otra construcción que aparezca en la lista anterior.

Teorema de equivalencia de compás (traducción en círculo) [ editar ]

Artículo principal: Teorema de equivalencia de brújula.

La capacidad de traducir, o copiar, un círculo a un nuevo centro es vital en estas pruebas y fundamental para establecer la veracidad del teorema. La creación de un nuevo círculo con el mismo radio que el primero, pero centrado en un punto diferente, es la característica clave que distingue a la brújula colapsante de la brújula moderna y rígida. La equivalencia de una brújula colapsante y una brújula rígida fue demostrada por Euclid (Libro I, Propuesta 2 de Los Elementos ) utilizando una brújula de regla y colapsable cuando, esencialmente, construye una copia de un círculo con un centro diferente. Esta equivalencia también se puede establecer con la brújula sola.

Reflejando un punto a través de una línea [ editar ]

Simetría puntual

• Dado un segmento de línea AB y un punto C que no está en la línea determinada por ese segmento, construya la imagen de C al reflexionar sobre esta línea.

1. Construir dos círculos: uno centrado en A y uno centrado en B , tanto pasando a través de C .
2. D , el otro punto de intersección de los dos círculos, es el reflejo de C a través de la línea AB . Si C = D (es decir, hay un punto único de intersección de los dos círculos), C se encuentra en la línea AB y es igual a su propio reflejo (en contra de lo que se supone).

Extendiendo la longitud de un segmento de línea [ editar ]

Una construcción de brújula única que duplica la longitud del segmento AB

• Dado un segmento de línea AB, encuentre un punto C en la línea ABtal que B sea ​​el punto medio del segmento de línea AC . ^[13]

1. Construya el punto D como la intersección de los círculos A ( B )y B ( A ) . (∆ ABD es un triángulo equilátero.)
2. Construya el punto E ≠ A como la intersección de los círculos D ( B ) y B ( D ) . (∆ DBE es un triángulo equilátero.)
3. Finalmente, construya el punto C ≠ D como la intersección de los círculos B ( E ) y E ( B ) . (∆ EBC es un triángulo equilátero, y los tres ángulos en B muestran que A , B y C son colineales.)

Esta construcción se puede repetir tantas veces como sea necesario para encontrar un punto Q de modo que la longitud del segmento de línea AQ = n ⋅ la longitud del segmento de línea AB para cualquier entero positivo n .

Inversión en un círculo [ editar ]

Punto de inversión en un círculo.

• Dado un círculo B ( r ) , para un radio r (en negro) y un punto D (≠ B ) construya el punto I que es el inverso de D en el círculo. ^[14]

1. Dibuja un círculo D ( B ) (en rojo).
2. Suponga que el círculo rojo intersecta el círculo negro en E y E '(si los círculos no se intersecan en dos puntos, vea más abajo).
3. Construya dos nuevos círculos E ( B ) y E ' ( B ) (en azul claro).
4. Los círculos de color azul claro se cortan en B y en otro punto I ≠ B .
5. El punto I es el inverso deseado de D en el círculo negro.

El punto I es tal que el radio r de B ( r ) es a IB como DB es al radio; o IB / r = r / DB .

En el caso de que falle la construcción anterior (es decir, el círculo rojo y el círculo negro no se intersecan en dos puntos), ^[15] encuentre un punto Q en la línea BD para que la longitud del segmento de línea BQ sea ​​una integral positiva múltiple, digamos n , de la longitud de BD y es mayor que r / 2 (esto es posible por el axioma de Archimede). Encuentre Q ' el inverso de Q en el círculo B ( r ) como arriba (los círculos rojo y negro ahora deben intersecarse en dos puntos). El punto I ahora se obtiene extendiendo BQ 'de modo que BI = n ⋅ BQ ' .

Determinar el centro de un círculo a través de tres puntos [ editar ]

Construcción de brújula del centro de un círculo a través de tres puntos (A, B, C)

• Dados tres puntos no colineales A , B y C , encuentra el centro O del círculo que determinan. ^[dieciséis]

1. Construya el punto D , el inverso de C en el círculo A ( B ) .
2. Representativas A en la línea BD al punto X .
3. O es el inverso de X en el círculo A ( B ) .

Intersección de dos líneas no paralelas (construcción # 3) [ editar ]

Construcción de solo compás de la intersección de dos líneas (no se muestran todos los pasos de construcción)

• Líneas no paralelas dadas AB y CD , encuentran su punto de intersección, X . ^[dieciséis]

1. Seleccione el círculo O ( r ) de radio arbitrario cuyo centro O no se encuentra en ninguna de las líneas.
2. Invierta los puntos A y B en el círculo O ( r ) a los puntos A ' y B'respectivamente.
3. La línea AB se invierte al círculo que pasa por O , A ' y B' . Encuentra el centro E de este círculo.
4. Invierta los puntos C y D en el círculo O ( r ) a los puntos C ' y D' respectivamente.
5. La línea CD se invierte al círculo que pasa por O , C ' y D' . Encuentra el centro F de este círculo.
6. Sea Y ≠ O la intersección de los círculos E ( O ) y F ( O ) .
7. X es el inverso de Y en el círculo O ( r ) .

Intersección de una línea y un círculo (construcción # 4) [ editar ]

La construcción de la brújula de los puntos de intersección de una línea y un círculo se divide en dos casos dependiendo de si el centro del círculo es o no colineal con la línea.

El centro del círculo no es colineal con la línea [ editar ]

Supongamos que el centro del círculo no se encuentra en la línea.

Intersección línea-círculo (caso no colineal)

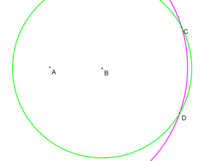
• Dado un círculo C ( r ) (en negro) y una línea AB . Deseamos construir los puntos de intersección, P y Q , entre ellos (si existen). ^[8] [17]

1. Construya el punto D , que es el reflejo del punto C a través de la línea AB . (Véase más arriba). Bajo el supuesto de este caso, C ≠ D .
2. Construye un círculo D ( r ) (en rojo). (Ver arriba, equivalencia de la brújula).
3. Las intersecciones de círculo C ( r ) y el nuevo círculo rojo son puntos P y Q .
4. P y Q son los puntos de intersección del círculo C ( r ) y la línea AB .

También se puede dar una construcción alternativa, utilizando inversión de círculo. ^[dieciséis]

• Dado un círculo C ( r ) y una línea AB . Deseamos construir los puntos de intersección, P y Q , entre ellos (si existen).

1. Invierta los puntos A y B en el círculo C ( r ) a los puntos A ' y B' respectivamente.
2. La línea AB se invierte al círculo que pasa por C , A ' y B' . Encuentra el centro E de este círculo.
3. P y Q son los puntos de intersección de los círculos C ( r ) y E ( C ) . ^[18]

El centro del círculo es colineal con la línea [ editar ]

Compás solo construcción de la intersección de un círculo y una línea (centro del círculo en la línea)

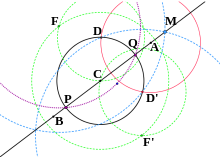
• Dado el círculo C ( D ) cuyo centro C se encuentra en la línea AB , encuentre los puntos P y Q , los puntos de intersección del círculo y la línea. ^[19]

1. Construya el punto D ' ≠ D como la otra intersección de los círculos A ( D ) y C ( D ) .
2. Construya el punto F como la intersección de los círculos C ( DD ' ) y D ( C ) . ( F es el cuarto vértice del paralelogramo CD'DF ).
3. Construya el punto F ' como la intersección de los círculos C ( DD' ) y D ' ( C ) . ( F ' es el cuarto vértice del paralelogramo CDD'F' .)
4. Construya el punto M como una intersección de los círculos F ( D ' ) y F' ( D ) . ( M se encuentra en AB.)
5. Los puntos P y Q son las intersecciones de los círculos F ( CM ) y C ( D ) .

Por lo tanto, se ha demostrado que toda la construcción básica que se puede realizar con una regla y una brújula se puede hacer solo con una brújula, siempre que se entienda que una línea no se puede trazar literalmente, sino simplemente definirse por dos puntos.

Teorema de Monge. La intersección de las líneas rojas, la de las líneas azules y la de las líneas verdes son colineales, todas caen en la línea negra.

En geometría , el teorema de Monge , que lleva el nombre de Gaspard Monge , establece que para tres círculos en un plano, ninguno de los cuales está completamente dentro de uno de los otros, los puntos de intersección de cada uno de los tres pares de líneas tangentes externas son colineales .

Para cualquiera de los dos círculos en un plano, una tangente externa es una línea que es tangente a ambos círculos pero que no pasa entre ellos. Hay dos líneas tangentes externas de este tipo para cualquiera de los dos círculos. Cada par tiene un punto de intersección único en el plano euclidiano extendido . El teorema de Monge establece que los tres puntos que da cada círculo están siempre en línea recta. En el caso de que dos de los círculos tengan el mismo tamaño, las dos líneas tangentes externas son paralelas. En este caso, el teorema de Monge afirma que los otros dos puntos de intersección deben estar en una línea paralela a esas dos tangentes externas. En otras palabras, si se considera que las dos tangentes externas se intersecan en el punto en el infinitoLuego, los otros dos puntos de intersección deben estar en una línea que pasa por el mismo punto en el infinito, de modo que la línea entre ellos tome el mismo ángulo que la tangente externa.

La prueba más simple emplea una analogía tridimensional. ^[1] Dejen que los tres círculos correspondan a tres esferas de los mismos radios; los círculos corresponden a los ecuadores que resultan de un plano que pasa a través de los centros de las esferas. Las tres esferas se pueden emparedar únicamente entre dos planos. Cada par de esferas define un cono que es externamente tangente a ambas esferas, y el vértice de este cono corresponde al punto de intersección de las dos tangentes externas, es decir, el centro homotético externo . Como una línea del cono se encuentra en cada plano, el vértice de cada cono debe estar en ambos planos y, por lo tanto, en algún lugar de la línea de intersección de los dos planos. Por lo tanto, los tres centros homotéticos externos son colineales.

El teorema de Monge también se puede probar usando el teorema de Desargues . Otra prueba fácil utiliza el teorema de Menelao , ya que las relaciones se pueden calcular con los diámetros de cada círculo, que se eliminarán mediante formas cíclicas cuando se use el teorema de Menelao. El teorema de Desargues también afirma que 3 puntos se encuentran en una línea, y tiene una prueba similar utilizando la misma idea de considerarlo en 3 en lugar de 2 dimensiones y escribiendo la línea como una intersección de 2 planos.