GEOMETRÍA - TEOREMAS EN GEOMETRÍA

□ M ₁ M ₂ M ₃ M ₄ es un rectángulo.

En geometría , el teorema japonésestablece que los centros de los incircles de ciertos triángulos dentro de un cuadrilátero cíclico son vértices de un rectángulo .

Al triangular un cuadrilátero cíclico arbitrario por sus diagonales, se obtienen cuatro triángulos superpuestos (cada diagonal crea dos triángulos). Los centros de los incircles de esos triángulos forman un rectángulo.

Específicamente, deja □ ABCD sea un cuadrilátero cíclico arbitraria y dejar que M ₁ , M ₂ , M ₃ , M ₄ sea los incentros de los triángulos △ ABD , △ ABC , △ BCD , △ ACD . Entonces el cuadrilátero formado por M ₁ , M ₂ , M ₃ , M ₄es un rectángulo.

Tenga en cuenta que este teorema se puede extender fácilmente para demostrar el teorema japonés para polígonos cíclicos . Para probar el caso del cuadrilátero, simplemente construya el paralelogramo tangente a las esquinas del rectángulo construido, con lados paralelos a las diagonales del cuadrilátero. La construcción muestra que el paralelogramo es un rombo, que es equivalente a mostrar que las sumas de los radios de los incirculos tangentes a cada diagonal son iguales.

El caso cuadrilátero prueba inmediatamente el caso general por inducción en el conjunto de particiones triangulares de un polígono general.

En geometría , el teorema de Jung es una desigualdad entre el diámetro de un conjunto de puntos en cualquier espacio euclidiano y el radio de la bola envolvente mínima de ese conjunto. Lleva el nombre de Heinrich Jung , quien primero estudió esta desigualdad en 1901.

Declaración [ editar ]

Considera un conjunto compacto.

$${\ displaystyle K \ subconjunto \ mathbb {R} ^ {n}}

y deja

$${\ displaystyle d = \ max \ nolimits _ {p, q \ en K} \ | pq \ | _ {2}}

Sea el diámetro de K , es decir, la distancia euclidiana más grande entre cualquiera de sus dos puntos. El teorema de Jung establece que existe una bola cerrada con radio.

$${\ displaystyle r \ leq d {\ sqrt {\ frac {n} {2 (n + 1)}}}}

que contiene k . El caso límite de igualdad es alcanzado por el n - simplex regular .

Teorema de Jung en el plano [ editar ]

El más común es el caso del teorema de Jung en el plano , que es n  = 2. En este caso, el teorema establece que existe un círculo que encierra todos los puntos cuyo radio satisface

$${\ displaystyle r \ leq {\ frac {d} {\ sqrt {3}}}.}

No se puede mostrar un límite más estrecho en r : cuando K es un triángulo equilátero (o sus tres vértices), entonces

$${\ displaystyle r = {\ frac {d} {\ sqrt {3}}}.}

Espacios métricos generales [ editar ]

Para cualquier conjunto delimitado S en cualquier espacio métrico , d / 2 ≤ r ≤ d . La primera desigualdad es implicado por la desigualdad triangular para el centro de la bola y los dos puntos diametrales, y la segunda desigualdad sigue desde una bola de radio d centrada en cualquier punto del S contendrá todos S . En un espacio métrico uniforme , es decir, un espacio en el que todas las distancias son iguales, r = d . En el otro extremo del espectro, en un espacio métrico inyectivo como la distancia de Manhattan en el avión,r = d / 2: cualquiera de las dos bolas cerradas de radio d / 2 centradas en los puntos de S tienen una intersección no vacía, por lo tanto, todas esas bolas tienen una intersección común, y una bola de radio d / 2 centrada en un punto de esta intersección contiene todas de s . También se conocen versiones del teorema de Jung para diversas geometrías no euclidianas (véase, por ejemplo, Dekster 1995, 1997).

X (54) es el punto Kosnita del triángulo ABC.

En la geometría euclidiana , el teorema de Kosnita es una propiedad de ciertos círculos asociados con un triánguloarbitrario .

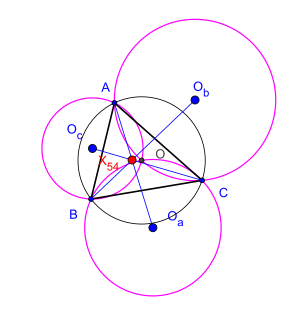
Dejar $${\ displaystyle ABC} ser un triángulo arbitrario, $${\ displaystyle O}su circuncentro y$${\ displaystyle O_ {a}, O_ {b}, O_ {c}} Son los circuncentrantes de tres triángulos. $${\ displaystyle OBC}, $${\ displaystyle OCA}y $${\ displaystyle OAB}respectivamente. El teorema afirma que las tres líneas rectas $${\ displaystyle AO_ {a}}, $${\ displaystyle BO_ {b}}y $${\ displaystyle CO_ {c}}son concurrentes. ^[1] Este resultado fue establecido por el matemático rumano Cezar Coşniţă (1910-1962). ^[2]

Su punto de concurrencia se conoce como el punto Kosnita del triángulo (nombrado por Rigby en 1997). Es el conjugado isogonal del centro de nueve puntos . ^[3] [4] Es el centro del triángulo $${\ displaystyle X (54)}en la lista de Clark Kimberling . ^[5]Este teorema es un caso especial del teorema de Dao en seis circuncentros asociados con un hexágono cíclico en. 

teorema de Lickorish-Wallace en la teoría de 3-múltiplos establece que cualquier 3-múltiple cerrado , orientable y conectado se puede obtener al realizar la cirugía Dehn en un enlace enmarcado en la esfera 3 con ± 1 coeficientes de cirugía. Además, se puede suponer que cada componente del enlace no tiene nudos.

El teorema fue probado a principios de la década de 1960 por WBR Lickorish y Andrew H. Wallace , independientemente y por diferentes métodos. Prueba de Lickorish descansó en el teorema de giro Lickorish , que establece que cualquier orientable automorphism de un orientable cerrada superficie se genera por giros Dehn a lo largo de 3 g - 1 curvas cerradas simples específicos en la superficie, donde g denota el género de la superficie. La prueba de Wallace era más general e involucraba la adición de asas al límite de una bola de dimensión superior.

Un corolario del teorema es que cada 3-manifold cerrado y orientable limita un 4-manifold compacto simplemente conectado .

Al utilizar su trabajo sobre automorfismos de superficies no orientables, Lickorish también demostró que cada colector de 3 conectado, no orientable y conectado se obtiene mediante la cirugía de Dehn en un enlace en el haz de 2 esferas no orientable sobre el círculo. Al igual que en el caso orientable, la cirugía se puede realizar de una manera especial que permita concluir que cada colector de 3 colectores, no orientables, cerrado, es un colector de 4 compacto.

el teorema de Liouville , probado por Joseph Liouville en 1850 , es un teorema de rigidezsobre los mapas conformales en el espacio euclidiano . Afirma que cualquier mapeo conforme suave en un dominio de R ⁿ , donde n  > 2, se puede expresar como una composición de traslaciones , similitudes , transformaciones ortogonales e inversiones : son transformaciones de Möbius (en n dimensiones). ^[1] [2]Este teorema limita severamente la variedad de posibles asignaciones conformes en R ³ y espacios de dimensiones superiores. Por el contrario, las asignaciones conformes en R ² pueden ser mucho más complicadas; por ejemplo, todos los dominios planares simplemente conectados son conformamente equivalentes , según el teorema de asignación de Riemann .

Las generalizaciones del teorema son válidas para transformaciones que son solo débilmente diferenciables ( Iwaniec y Martin 2001 , Capítulo 5). El enfoque de tal estudio es el sistema no lineal Cauchy-Riemann que es una condición necesaria y suficiente para que un mapeo suave ƒ  → Ω →  R ⁿ sea ​​conforme:

$${\ displaystyle Df ^ {T} Df = \ left | \ det Df \ right | ^ {2 / n} I}

donde Df es la derivada jacobiana , T es la transposición de la matriz y I es la matriz de la identidad. Una solución débil de este sistema se define como un elemento ƒ del espacio Sobolev W 1, n
loc ( Ω , R ⁿ ) con determinante jacobiano no negativo en casi todas partes , de modo que el sistema Cauchy-Riemann se mantiene en casi todos los puntos de Ω. El teorema de Liouville es que cada solución débil (en este sentido) es una transformación de Möbius, lo que significa que tiene la forma

${\displaystyle f(x)=b+{\frac {\alpha A(x-a)}{|x-a|^{\epsilon }}}}$

donde a , b son vectores en R ⁿ , α es un escalar, A es una matriz de rotación y ε = 0 o 2. De manera equivalente, cualquier mapa cuasiconformal de un dominio en el espacio euclidiano que también es conforme es una transformación de Möbius. Esta declaración equivalente justifica el uso del espacio Sobolev W ^1, n , ya que ƒ  ∈  W 1, n
loc ( Ω , R ⁿ ) luego sigue la condición geométrica de conformidad y la caracterización ACL del espacio Sobolev. Sin embargo, el resultado no es óptimo: en dimensiones pares n  = 2k , el teorema también se aplica a soluciones que solo se asume que están en el espacio W 1, k
loc , y este resultado es claro en el sentido de que hay soluciones débiles del sistema Cauchy-Riemann en W ^1, p para cualquier p  <  k que no son transformaciones de möbius. En dimensiones impares, se sabe que W ^1, n no es óptimo, pero no se conoce un resultado claro.

Los resultados de rigidez similares (en el caso liso) se mantienen en cualquier colector conforme . El grupo de isometrías conformales de una variedad de Riemannian conformada en n dimensiones siempre tiene una dimensión que no puede exceder la del grupo conformal completo SO ( n +1,1). La igualdad de las dos dimensiones se mantiene exactamente cuando la variedad conforme es isométrica con la n- esfera o espacio proyectivo . Las versiones locales del resultado también son válidas: el álgebra de Lie de los campos de matanza conformal en un conjunto abierto tiene una dimensión menor o igual a la del grupo conformal, y se mantiene la igualdad si y solo si el conjunto abierto es localmente plano.