En geometría de 4 dimensiones , hay 9 politopos uniformes con simetría A 4 . Hay una forma regular auto-dual, la de 5 celdas con 5 vérticeS.
Simetría [ editar ]
A 4 simetría, o [3,3,3] es el orden 120, con Conway cuaternión notación + 1 / 60 [I × I ] 0,2 1 . Su estructura abstracta es el grupo simétrico S 5 . Tres formas con diagramas de Coxeter simétricos han extendido simetría, [[3,3,3]] de orden 240, y la notación Conway ± 1 / 60 [i × I ] 0,2, y el resumen estructura S 5 × C 2 .
Visualizaciones [ editar ]
Cada una puede visualizarse como proyecciones ortográficas simétricas en los planos de Coxeter del grupo A 4 de Coxeter y otros subgrupos. Se proporcionan tres proyecciones 2D del plano de Coxeter , para los grupos A 4 , A 3 , A 2 de Coxeter , que muestran el orden de simetría 5,4,3, y se duplicaron en órdenes A k iguales a 10,4,6 para los diagramas de Coxeter simétricos.
Las imágenes en 3D se dibujan como proyecciones de Schlegel , centradas en la celda en pos. 3, con una orientación consistente, y las 5 celdas en la posición 0 se muestran sólidas.
| # | Nombre | Diagrama de Coxeter y símbolosSchläfli | Gráficos de plano de cooxeter | Diagrama de schlegel | Red | |||
|---|---|---|---|---|---|---|---|---|
| A 4 [5] | A 3 [4] | A 2 [3] | Centrado entetraedro | Doble tetraedro centrado | ||||
| 1 | Pentacoron de 5 celdas | {3,3,3} |  |  |  |  |  | |
| 2 | rectificado de 5 celdas | r {3,3,3} |  | 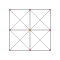 | 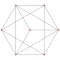 |  |  | |
| 3 | truncado de 5 celdas | t {3,3,3} |  |  |  |  |  | |
| 4 | de 5 celdas | rr {3,3,3} |  | 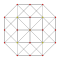 |  |  |  | |
| 7 | Cantitruncated 5-cell | tr {3,3,3} |  | 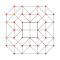 | 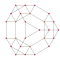 |  | 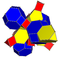 | |
| 8 | Runcitruncated 5 celdas | t 0,1,3 {3,3,3} |  |  |  |  |  | |
| # | Nombre | Diagrama de Coxeter y símbolosSchläfli | Gráficos de plano de cooxeter | Diagrama de schlegel | Red | ||
|---|---|---|---|---|---|---|---|
| A 4 [[5]] = [10] | A 3 [4] | A 2 [[3]] = [6] | Centrado en tetraedro | ||||
| 5 | * Runcinado en 5 celdas | t 0,3 {3,3,3} |  | 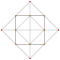 | 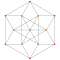 |  |  |
| 6 | * Bitruncated 5-célula decachoron | 2t {3,3,3} |  | 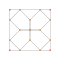 | 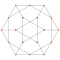 |  |  |
| 9 | * omnitruncado de 5 celdas | t 0,1,2,3 {3,3,3} |  | 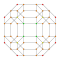 | 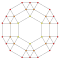 |  | 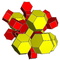 |
Coordenadas [ editar ]
Las coordenadas de los 4-politopos uniformes con simetría pentacórica se pueden generar como permutaciones de enteros simples en el espacio 5, todos en hiperplanos con vector normal (1,1,1,1,1). El grupo A 4 Coxeter es palindrómico , por lo que los politopos repetidos existen en pares de configuraciones duales. Hay 3 posiciones simétricas y 6 pares que hacen un total de 15 permutaciones de uno o más anillos. Los 15 se enumeran aquí en orden aritmético binario para la claridad de la generación de coordenadas a partir de los anillos en cada diagrama de Coxeter correspondiente.
El número de vértices se puede deducir aquí a partir de las permutaciones del número de coordenadas, alcanzando un máximo de 5 factorial para la forma omnitruncada con 5 valores de coordenadas únicos.
| # | Punto base | Nombre (nombre simétrico) | Diagrama de cooxeter | Vértices | |
|---|---|---|---|---|---|
| 1 | (0, 0, 0, 0, 1) (1, 1, 1, 1, 0) | 5 celdas trirectificadas 5 celdas | 5 | 5! / (4!) | |
| 2 | (0, 0, 0, 1, 1) (1, 1, 1, 0, 0) | Rectificado de 5 celdas Birectificado de 5 celdas | 10 | 5! / (3! 2!) | |
| 3 | (0, 0, 0, 1, 2) (2, 2, 2, 1, 0) | Truncado 5 celdas Tritruncado 5 celdas | 20 | 5! / (3!) | |
| 5 | (0, 1, 1, 1, 2) | Runcinado en 5 celdas | 20 | 5! / (3!) | |
| 4 | (0, 0, 1, 1, 2) (2, 2, 1, 1, 0) | Células de 5 celdas bicelizadas de 5 celdas | 30 | 5! / (2! 2!) | |
| 6 | (0, 0, 1, 2, 2) | Bitruncado de 5 celdas | 30 | 5! / (2! 2!) | |
| 7 | (0, 0, 1, 2, 3) (3, 3, 2, 1, 0) | Cantitruncated 5-cell Bicantitruncated 5-cell | 60 | 5! / 2! | |
| 8 | (0, 1, 1, 2, 3) (3, 2, 2, 1, 0) | Runcitruncated 5-cell Runcicantellated 5-cell | 60 | 5! / 2! | |
| 9 | (0, 1, 2, 3, 4) | Omnitruncated 5-cell | 120 | 5! | |
En geometría de 5 dimensiones , hay 19 politopos uniformes con simetría A 5 . Hay una forma regular auto-dual, el 5-simplex con 6 vértices.
Cada una puede visualizarse como proyecciones ortográficas simétricas en los planos de Coxeter del grupo A 5 de Coxeter y otros subgrupos.
Gráficos [ editar ]
Se pueden realizar proyecciones ortográficas simétricas de estos 19 politopos en los planos de cooxímetro A 5 , A 4 , A 3 , A 2 . Las gráficas k tienen simetría [k + 1] . Incluso para k y los diagramas simétricamente de nodado_1, la simetría se duplica a [2 (k + 1)] .
Estos 19 politopos se muestran cada uno en estos 4 planos de simetría, con vértices y bordes dibujados, y vértices coloreados por el número de vértices superpuestos en cada posición proyectiva.
| # | Gráficos de plano de cooxeter | Diagrama de Coxeter-Dynkin Símbolo Schläfli Nombre | |||
|---|---|---|---|---|---|
| [6] | [5] | [4] | [3] | ||
| Un 5 | Un 4 | Un 3 | Un 2 | ||
| 1 |  |  |  |  | {3,3,3,3} 5-simplex (hix) |
| 2 |  |  |  |  | t 1 {3,3,3,3} or r {3,3,3,3} Rectificado 5-simplex (rix) |
| 3 |  |  | 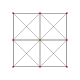 |  | t 2 {3,3,3,3} o 2r {3,3,3,3} Birectified 5-simplex (punto) |
| 4 |  |  |  |  | t 0,1 {3,3,3,3} o t {3,3,3,3} Truncado 5-simplex (tix) |
| 5 |  |  |  |  | t 1,2 {3,3,3,3} o 2t {3,3,3,3} Bitruncated 5-simplex (bittix) |
| 6 |  |  |  | 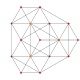 | t 0,2 {3,3,3,3} o rr {3,3,3,3} 5-simplex cantellated (sarx) |
| 7 |  |  |  |  | t 1,3 {3,3,3,3} o 2rr {3,3,3,3} 5-simplex bicantellated (sibrid) |
| 8 |  |  | 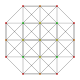 |  | t 0,3 {3,3,3,3} Runcinado 5-simplex (spix) |
| 9 |  |  | 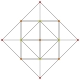 |  | t 0,4 {3,3,3,3} o 2r2r {3,3,3,3} Esterilizado 5-simplex (scad) |
| 10 |  |  |  |  | t 0,1,2 {3,3,3,3} o tr {3,3,3,3} Cantitruncated 5-simplex (garx) |
| 11 |  |  |  |  | t 1,2,3 {3,3,3,3} o 2tr {3,3,3,3} Bicantitruncated 5-simplex (gibrid) |
| 12 |  |  | 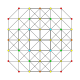 |  | t 0,1,3 {3,3,3,3} Runcitruncated 5-simplex (pattix) |
| 13 |  |  | 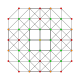 |  | t 0,2,3 {3,3,3,3} Runcicantellated 5-simplex (pirx) |
| 14 |  |  |  |  | t 0,1,4 {3,3,3,3} 5-simplex esteritruncated (cappix) |
| 15 |  |  |  |  | t 0,2,4 {3,3,3,3} 5-simplex esterilizado (tarjeta) |
| dieciséis |  |  | 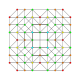 |  | t 0,1,2,3 {3,3,3,3} Runcicantitruncated 5-simplex (gippix) |
| 17 |  |  | 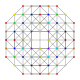 |  | t 0,1,2,4 {3,3,3,3} 5-simplex estericantitruncated (cograx) |
| 18 |  |  |  |  | t 0,1,3,4 {3,3,3,3} 5-simplex esteriruncitruncated (captid) |
| 19 |  |  |  |  | t 0,1,2,3,4 {3,3,3,3} Omnitruncated 5-simplex (gocad) |
| A5 politopos | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 t 0 |  t 1 |  t 2 |  t 0,1 |  t 0,2 |  t 1,2 |  t 0,3 | |||||
 t 1,3 |  t 0,4 |  t 0,1,2 |  t 0,1,3 |  t 0,2,3 |  t 1,2,3 |  t 0,1,4 | |||||
 t 0,2,4 |  t 0,1,2,3 |  t 0,1,2,4 |  t 0,1,3,4 |  t 0,1,2,3,4 | |||||||
En geometría de 6 dimensiones , hay 35 politopos uniformes con simetría A 6 . Hay una forma regular auto-dual, el 6-simplex con 7 vértices.
Cada una puede visualizarse como proyecciones ortográficas simétricas en los planos de Coxeter del grupo A 6 Coxeter y otros subgrupos.
Gráficos [ editar ]
Se pueden hacer proyecciones ortográficas simétricas de estos 35 politopos en los planos de cooxímetro A 6 , A 5 , A 4 , A 3 , A 2 . Las gráficas k tienen simetría [k + 1] . Para los diagramas de anillos pares y simétricos, la simetría se duplica a [2 (k + 1)] .
Estos 35 politopos se muestran cada uno en estos 5 planos de simetría, con vértices y bordes dibujados, y vértices coloreados por el número de vértices superpuestos en cada posición proyectiva.
| # | A 6 [7] | A 5 [6] | A 4 [5] | A 3 [4] | A 2 [3] | Diagrama de Coxeter-Dynkin Símbolo Schläfli Nombre |
|---|---|---|---|---|---|---|
| 1 |  |  |  |  |  | t 0 {3,3,3,3,3} 6-simplex Heptapeton (salto) |
| 2 |  | 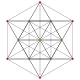 |  |  |  | t 1 {3,3,3,3,3} Rectificado 6-simplex Heptapetón rectificado (ril) |
| 3 |  |  |  |  | 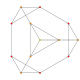 | t 0,1 {3,3,3,3,3} Heptapetón truncado 6-simplex truncado (hasta) |
| 4 |  |  |  |  |  | t 2 {3,3,3,3,3} Heptapetón birectificado 6-simplex bifurcado (brillar) |
| 5 |  |  |  |  |  | t 0,2 {3,3,3,3,3} Heptapetónrombado pequeño (sril) 6-simplex cantellated |
| 6 |  |  |  |  | 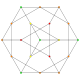 | t 1,2 {3,3,3,3,3} Bitruncado 6-simplex Heptapetón bitruncado (batal) |
| 7 |  |  |  | 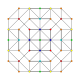 |  | t 0,1,2 {3,3,3,3,3} 6-simplex cantitruncado Gran heptapetón rombado (gril) |
| 8 |  |  |  |  |  | t 0,3 {3,3,3,3,3} Heptapetón prismado pequeño y runcinado 6 ( simplificado) |
| 9 |  | 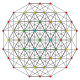 |  |  |  | t 1,3 {3,3,3,3,3} Heptapeton birhombatedpequeño de 6-simplex (sabril) |
| 10 |  | 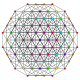 |  |  |  | t 0,1,3 {3,3,3,3,3} Heptapetón prismatotruncado 6- simpluncuncuncuncated (patal) |
| 11 |  |  |  |  |  | t 2,3 {3,3,3,3,3} Tetradecapeton tritruncado 6-simplex (fe) |
| 12 |  |  |  | 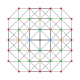 |  | t 0,2,3 {3,3,3,3,3} Heptapetón Prismatorhombated Prismatorhombated de Runcicantellated (pril) |
| 13 |  |  | 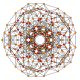 |  | 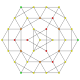 | t 1,2,3 {3,3,3,3,3} Heptapetón gran birhombado bicantitruncado (gabril) |
| 14 |  | 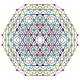 |  |  | 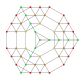 | t 0,1,2,3 {3,3,3,3,3} Heptapetón prismado granular (6) simplificado (6). |
| 15 |  |  |  |  |  | t 0,4 {3,3,3,3,3} Stericated 6-simplex Pequeño heptapeton cellated (fiscal) |
| dieciséis |  | 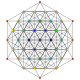 | 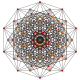 |  |  | t 1,4 {3,3,3,3,3} Biruncinated 6-simplex Biprismato-tetradecapeton pequeño (sibpof) |
| 17 |  |  |  |  | 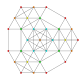 | t 0,1,4 {3,3,3,3,3} Heptapetón cellitruncated 6-simplex esteritruncated (catal) |
| 18 |  |  |  | 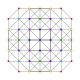 |  | t 0,2,4 {3,3,3,3,3} Heptapetón celularpurificado 6-simplex esterilizado (cral) |
| 19 |  |  |  |  | 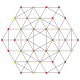 | t 1,2,4 {3,3,3,3,3} Heptapeton biprismatorbifrismatorbuncuncuncuncir buncril (bapril) |
| 20 |  |  |  |  | 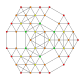 | t 0,1,2,4 {3,3,3,3,3} Heptapetón de 6-simplex estrictamente esterricantuncuncado o hepatratectado (cagral) |
| 21 |  |  |  |  |  | t 0,3,4 {3,3,3,3,3} Heptapetón Celliprismated 6-simplex esteriruncinado (copal) |
| 22 |  |  | 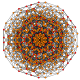 |  |  | t 0,1,3,4 {3,3,3,3,3} Heptapeton celiprismatotruncated 6-simplex Steriruncitruncated (captal) |
| 23 |  |  | 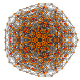 |  | 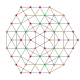 | t 0,2,3,4 {3,3,3,3,3}Heptapetón (copril) del celliprismator 6-simplex esterilizado y esterilizado. |
| 24 |  |  |  |  |  | t 1,2,3,4 {3,3,3,3,3} Biruncicantitruncated 6-simplex Gran biprismato-tetradecapeton (gibpof) |
| 25 |  | 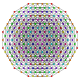 |  |  | 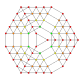 | t 0,1,2,3,4 {3,3,3,3,3} Heptapetón celladogranulado (6-simplex) esteriruncicantitruncated (gacal) |
| 26 |  |  |  |  | 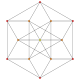 | t 0,5 {3,3,3,3,3} 6-simplex pentelilado Teri -tetradecapeton pequeño (staf) |
| 27 |  |  | 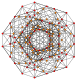 | 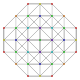 | 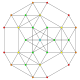 | t 0,1,5 {3,3,3,3,3} Heptapetón pentitruncado 6-simplex Tericellated (tocal) |
| 28 |  |  |  |  |  | t 0,2,5 {3,3,3,3,3} Heptapetón teriprismado 6-simplex penticantelilado (tapal) |
| 29 |  |  |  |  |  | t 0,1,2,5 {3,3,3,3,3} Heptapetón terigreatorhombateado de 6-simplex penticantitruncated (togral) |
| 30 |  | 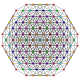 | 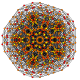 |  | 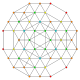 | t 0,1,3,5 {3,3,3,3,3} Heptapetón pentiruncitruncated 6-simplex Tericellirhombated (tocral) |
| 31 |  |  |  |  |  | t 0,2,3,5 {3,3,3,3,3} Pentiruncicantellated 6-simplex Teriprismatorhombi-tetradecapeton (taporf) |
| 32 |  |  |  |  | 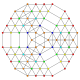 | t 0,1,2,3,5 {3,3,3,3,3} Heptapetónterigreatoprismadopentiruncicantitruncated 6-simplex (tagopal) |
| 33 |  |  |  |  |  | t 0,1,4,5 {3,3,3,3,3} Pentisteritruncated 6-simplex tericellitrunki-tetradecapeton (tactaf) |
| 34 |  |  |  |  | 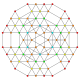 | t 0,1,2,4,5 {3,3,3,3,3} hepericpeton pentericéricoantuncuncado 6-simplex tericelligreatorhombated (tacogral) |
| 35 |  |  |  |  |  | t 0,1,2,3,4,5 {3,3,3,3,3} Omnitruncado 6-simplex Gran teri-tetradecapeton (gotaf) |
No hay comentarios:
Publicar un comentario