ARTÍCULOS DE MATEMÁTICAS

En geometría de 7 dimensiones , hay 71 politopos uniformes con simetría A ₇ . Hay una forma regular auto-dual, el 7-simplex con 8 vértices.

Cada una puede visualizarse como proyecciones ortográficas simétricas en los planos de Coxeter del grupo A ₇ Coxeter y otros subgrupos.

Gráficos [ editar ]

Las proyecciones ortográficas simétricas de estos 135 politopos se pueden realizar en los planos de cooxímetro A ₇ , A ₆ , A ₅ , A ₄ , A ₃ , A ₂ . A _k tiene simetría [k + 1] . Incluso para k y diagramas simétricamente anillados, la simetría se duplica a [2 (k + 1)] .

Estos 63 politopos se muestran cada uno en estos 6 planos de simetría, con vértices y bordes dibujados, y vértices coloreados por el número de vértices superpuestos en cada posición proyectiva.

#	Diagrama de Coxeter-Dynkin  Schläfli símbolo  nombre de Johnson	A k graficas de proyeccion ortogonal
		A 7 [8]	A 6 [7]	A 5 [6]	A 4 [5]	A 3 [4]	A 2 [3]
1	t 0 {3,3,3,3,3,3}  7-simplex
2	t 1 {3,3,3,3,3,3}  Rectificado 7-simplex
3	t 2 {3,3,3,3,3,3}  Birectified 7-simplex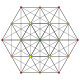
4	t 3 {3,3,3,3,3,3}  Trirectified 7-simplex
5	t 0,1 {3,3,3,3,3,3}  Truncado 7-simplex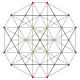
6	t 0,2 {3,3,3,3,3,3} 7-simplexcantellated
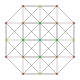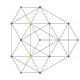7	t 1,2 {3,3,3,3,3,3}  Bitruncado 7-simplex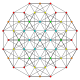
8	t 0,3 {3,3,3,3,3,3}  Runcinado 7-simplex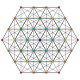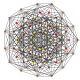
9	t 1,3 {3,3,3,3,3,3}  Bicantellated 7-simplex
10	t 2,3 {3,3,3,3,3,3}  tritruncado 7-simplex
11	t 0,4 {3,3,3,3,3,3}  7-simplex esterilizado
12	t 1,4 {3,3,3,3,3,3}  Biruncinado 7-simplex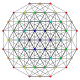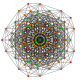
13	t 2,4 {3,3,3,3,3,3}  Tricantellated 7-simplex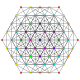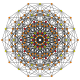
14	t 0,5 {3,3,3,3,3,3} Pentellated 7-simplex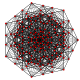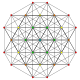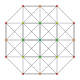
15	t 1,5 {3,3,3,3,3,3}  7-simplex bistérico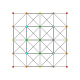
dieciséis	t 0,6 {3,3,3,3,3,3}  Hexicated 7-simplex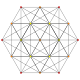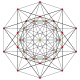
17	t 0,1,2 {3,3,3,3,3,3}  Cantitruncado 7-simplex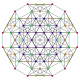
18	t 0,1,3 {3,3,3,3,3,3}  Runcitruncated 7-simplex
19	t 0,2,3 {3,3,3,3,3,3}  Runcicantellated 7-simplex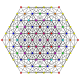
20	t 1,2,3 {3,3,3,3,3,3}  Bicantitruncated 7-simplex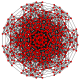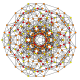
21	t 0,1,4 {3,3,3,3,3,3}  7-simplex esteritruncated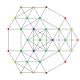
22	t 0,2,4 {3,3,3,3,3,3}  7-simplex esterilizados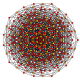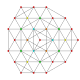
23	t 1,2,4 {3,3,3,3,3,3}  Biruncitruncated 7-simplex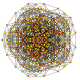
24	t 0,3,4 {3,3,3,3,3,3}  7-simplex esteriruncinado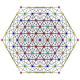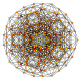
25	t 1,3,4 {3,3,3,3,3,3}  7-simplex bisuncicantellated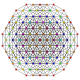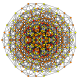
26	t 2,3,4 {3,3,3,3,3,3}  Tricantitruncated 7-simplex
27	t 0,1,5 {3,3,3,3,3,3}  Pentitruncado 7-simplex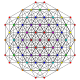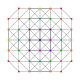
28	t 0,2,5 {3,3,3,3,3,3}  Penticantellated 7-simplex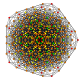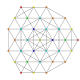
29	t 1,2,5 {3,3,3,3,3,3}  Bisteritruncado 7-simplex
30	t 0,3,5 {3,3,3,3,3,3}  Pentiruncinado 7-simplex
31	t 1,3,5 {3,3,3,3,3,3}  7-simplex bistericantellated
32	t 0,4,5 {3,3,3,3,3,3}  Pentistericated 7-simplex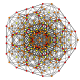
33	t 0,1,6 {3,3,3,3,3,3}  Hexitruncado 7-simplex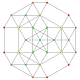
34	t 0,2,6 {3,3,3,3,3,3}  Hexicantellated 7-simplex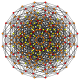
35	t 0,3,6 {3,3,3,3,3,3}  Hexiruncinado 7-simplex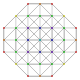
36	t 0,1,2,3 {3,3,3,3,3,3}  Runcicantitruncated 7-simplex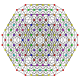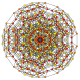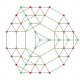
37	t 0,1,2,4 {3,3,3,3,3,3}  estericantitruncated 7-simplex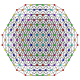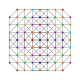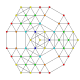
38	t 0,1,3,4 {3,3,3,3,3,3}  7-simplex esteriruncitruncated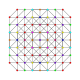
39	t 0,2,3,4 {3,3,3,3,3,3} 7-simplex esterilizados poresterilización  funcional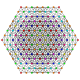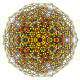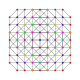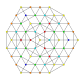
40	t 1,2,3,4 {3,3,3,3,3,3}  Biruncicantitruncated 7-simplex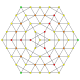
41	t 0,1,2,5 {3,3,3,3,3,3}  Penticantitruncated 7-simplex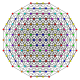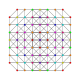
42	t 0,1,3,5 {3,3,3,3,3,3}  Pentiruncitruncated 7-simplex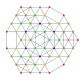
43	t 0,2,3,5 {3,3,3,3,3,3}  Pentiruncicantellated 7-simplex
44	t 1,2,3,5 {3,3,3,3,3,3}  Bistericantitruncated 7-simplex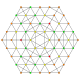
45	t 0,1,4,5 {3,3,3,3,3,3}  Pentisteritruncated 7-simplex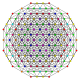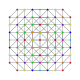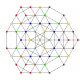
46	t 0,2,4,5 {3,3,3,3,3,3}  Pentiestericantellated 7-simplex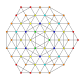
47	t 1,2,4,5 {3,3,3,3,3,3}  Bisteriruncitruncated 7-simplex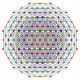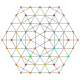
48	t 0,3,4,5 {3,3,3,3,3,3}  Pentisteriruncinado 7-simplex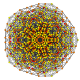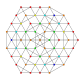
49	t 0,1,2,6 {3,3,3,3,3,3}  Hexicantitruncated 7-simplex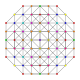
50	t 0,1,3,6 {3,3,3,3,3,3}  Hexiruncitruncated 7-simplex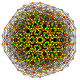
51	t 0,2,3,6 {3,3,3,3,3,3}  Hexiruncicantellated 7-simplex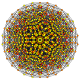
52	t 0,1,4,6 {3,3,3,3,3,3}  Hexisteritruncated 7-simplex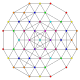
53	t 0,2,4,6 {3,3,3,3,3,3}  Hexistericantellated 7-simplex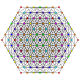
54	t 0,1,5,6 {3,3,3,3,3,3}  Hexipentitruncated 7-simplex
55	t 0,1,2,3,4 {3,3,3,3,3,3}  Steriruncicantitruncated 7-simplex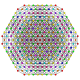
56	t 0,1,2,3,5 {3,3,3,3,3,3}  Pentiruncicantitruncated 7-simplex
57	t 0,1,2,4,5 {3,3,3,3,3,3}  Pentistericantitruncated 7-simplex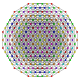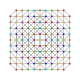
58	t 0,1,3,4,5 {3,3,3,3,3,3}  Pentisteriruncitruncated 7-simplex
59	t 0,2,3,4,5 {3,3,3,3,3,3}  Pentisteriruncicantellated 7-simplex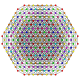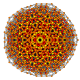
60	t 1,2,3,4,5 {3,3,3,3,3,3}  Bisteriruncicantitruncated 7-simplex
61	t 0,1,2,3,6 {3,3,3,3,3,3}  Hexiruncicantitruncated 7-simplex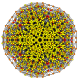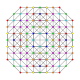
62	t 0,1,2,4,6 {3,3,3,3,3,3}  Hexistericantitruncated 7-simplex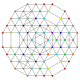
63	t 0,1,3,4,6 {3,3,3,3,3,3}  Hexisteriruncitruncated 7-simplex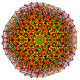
64	t 0,2,3,4,6 {3,3,3,3,3,3}  Hexisteriruncicantellated 7-simplex
sesenta y cinco	t 0,1,2,5,6 {3,3,3,3,3,3}  Hexipenticantitruncated 7-simplex
66	t 0,1,3,5,6 {3,3,3,3,3,3}  Hexipentiruncitruncated 7-simplex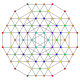
67	t 0,1,2,3,4,5 {3,3,3,3,3,3}  Pentisteriruncicantitruncated 7-simplex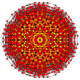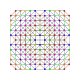
68	t 0,1,2,3,4,6 {3,3,3,3,3,3}  Hexisteriruncicantitruncated 7-simplex
69	t 0,1,2,3,5,6 {3,3,3,3,3,3}  Hexipentiruncicantitruncated 7-simplex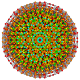
70	t 0,1,2,4,5,6 {3,3,3,3,3,3}  Hexipentistericantitruncated 7-simplex
71	t 0,1,2,3,4,5,6 {3,3,3,3,3,3}  Omnitruncated 7-simplex