ARTÍCULOS DE MATEMÁTICAS

Error de Abbe , llamado así por Ernst Abbe , también llamado error de seno , describe el aumento del error angular en la distancia. Por ejemplo, cuando uno mide un punto que está a 1 metro de distancia a 45 grados, un error angular de 1 grado corresponde a un error de posición de más de 1.745 cm, equivalente a un error de medición de distancia de 1.745%. ^[1]

En el diseño de la máquina, algunos componentes son particularmente sensibles a los errores angulares. Por ejemplo, leves desviaciones del paralelismo del eje del husillo de un torno al movimiento de la herramienta a lo largo del lecho de la máquina pueden llevar a un estrechamiento relativamente grande (no deseado) a lo largo de la parte (es decir, una parte no cilíndrica). Los calibradores a vernier no están libres de error de abe, mientras que los calibres de tornillo están libres de error de abbe. El error de Abbe es el producto del desplazamiento de Abbe y el seno del error angular en el sistema.

El error de abate puede ser perjudicial para el cómputo muerto .

Fórmula:

$${\ displaystyle \ epsilon = h \ sin \ theta}

$${\ displaystyle \ epsilon} el error.

$${\ displaystyle h} la distancia.

$${\ displaystyle \ theta} el ángulo.

Este artículo necesita citas adicionales para su verificación . Por favor, ayudar a mejorar este artículo mediante la adición de citas de fuentes confiables . El material sin fuente puede ser cuestionado y eliminado.  Encuentre fuentes:  "Condición sine de Abbe"  -  noticias  · periódicos  · libros  · erudito  ·JSTOR ( diciembre de 2009 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla)

Los ángulos de entrada y salida de cada rayo que pasa a través de un sistema de imágenes (recuadro gris) están relacionados. Cuando el sistema de imágenes obedece a la condición sinusoidal de Abbe, la proporción de los senos de estos ángulos es igual a la ampliación (lateral absoluta) del sistema.

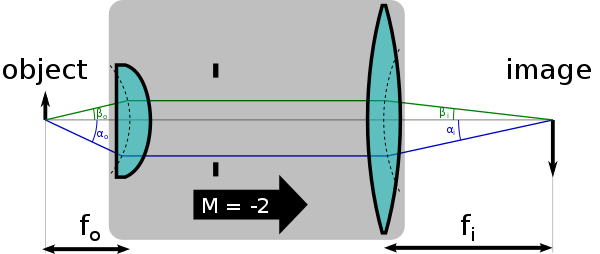
La condición sinusoidal de Abbe es una condición que debe cumplir una lente u otro sistema óptico para que pueda producir imágenes nítidas de objetos fuera de eje y en ejes. Fue formulado por Ernst Abbe en el contexto de los microscopios . ^[1]

La condición sine de Abbe dice que

el seno del ángulo del objeto-espacio$${\ textstyle \ alpha _ {o}} Debe ser proporcional al seno del ángulo del espacio de la imagen. $${\ textstyle \ alpha _ {i}}

Además, la relación es igual a la ampliación del sistema. En términos matemáticos esto es:

$${\ displaystyle {\ frac {\ sin \ alpha _ {o}} {\ sin \ alpha _ {i}}} = {\ frac {\ sin \ beta _ {o}} {\ sin \ beta _ {i} }} = | M |}

donde las variables $${\ textstyle (\ alpha _ {o}, \ beta _ {o})} son los ángulos (en relación con el eje óptico) de dos rayos cuando salen del objeto, y $${\ textstyle (\ alpha _ {i}, \ beta _ {i})}son los ángulos de los mismos rayos donde alcanzan el plano de la imagen (por ejemplo, el plano de película de una cámara). Por ejemplo, ($${\ textstyle \ alpha _ {o}, \ alpha _ {i})}podría representar un rayo paraxial (es decir, un rayo casi paralelo al eje óptico), y$${\ textstyle (\ beta _ {o}, \ beta _ {i})}podría representar un rayo marginal (es decir, un rayo con el ángulo más grande admitido por la apertura del sistema). Se dice que un sistema de imagen óptico para el cual esto es cierto para todos los rayos obedece la condición de seno de Abbe.

La ampliación y la condición sinusoidal de Abbe [ editar ]

Un sistema óptico de imágenes (caja gris) que obedece a la condición sinusoidal tiene una relación fija entre los senos de los ángulos de los rayos en la entrada y la salida del sistema. $${\ textstyle {\ frac {\ sin \ alpha _ {o}} {\ sin \ alpha _ {i}}} = M}. Esta relación es igual a la ampliación (M).

Usando el marco de la óptica de Fourier , podemos explicar fácilmente el significado de la condición de seno de Abbe. Decir que un objeto en el plano de objeto de un sistema óptico tiene una función de transmisión de la forma,T ( x _o , y _o ). Podemos expresar esta función de transmisión en términos de su transformada de Fourier como

$${\ displaystyle T (x_ {o}, y_ {o}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j (k_ {x} x_ {o} + k_ {y} y_ {o})} ~ dk_ {x} \, dk_ {y}.}

Ahora, supongamos por simplicidad que el sistema no tiene distorsión de imagen , de modo que las coordenadas del plano de la imagen están relacionadas linealmente con las coordenadas del plano del objeto a través de la relación

$${\ displaystyle x_ {i} = Mx_ {o} \,}

$${\ displaystyle y_ {i} = Mi_ {o} \,}

donde M es la ampliación del sistema . La transmitancia del plano de objeto anterior puede ahora reescribirse en una forma ligeramente modificada:

$${\ displaystyle T (x_ {o}, y_ {o}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j ((k_ {x} / M) (Mx_ {o}) + (k_ {y} / M) (My_ {o}))} ~ dk_ {x} \, dk_ {y}}

donde los diversos términos se han multiplicado y dividido simplemente en el exponente por M , la ampliación del sistema. Ahora, las ecuaciones se pueden sustituir por las coordenadas del plano de la imagen en términos de coordenadas del plano del objeto, para obtener,

$${\ displaystyle T (x_ {i}, y_ {i}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j ((k_ {x} / M) x_ {i} + ( k_ {y} / M) y_ {i})} ~ dk_ {x} \, dk_ {y}}

En este punto se puede proponer otra transformación de coordenadas ( i . E ., La condición sine Abbe) relativa el plano del objeto número de onda del espectro para el plano de imagen de número de onda del espectro como

$${\ displaystyle k_ {x} ^ {i} = {\ frac {k_ {x}} {M}}}

$${\ displaystyle k_ {y} ^ {i} = {\ frac {k_ {y}} {M}}}

para obtener la ecuación final para el campo del plano de la imagen en términos de coordenadas del plano de la imagen y números de referencia del plano de la imagen como:

$${\ displaystyle T (x_ {i}, y_ {i}) = M ^ {2} \ iint T (Mk_ {x} ^ {i}, Mk_ {y} ^ {i}) ~ e ^ {j (k_ {x} ^ {i} x_ {i} + k_ {y} ^ {i} y_ {i})} dk_ {x} ^ {i} \, dk_ {y} ^ {i}}

A partir de la óptica de Fourier , se sabe que los números de onda se pueden expresar en términos del sistema de coordenadas esféricas como

$${\ displaystyle k_ {x} = k \ sin \ theta \ cos \ varphi \,}

$${\ displaystyle k_ {y} = k \ sin \ theta \ sin \ varphi \,}

Si se considera un componente espectral para el cual $${\ displaystyle \ varphi = 0}, entonces la transformación de coordenadas entre el objeto y el plano de la imagen wavenumbers toma la forma

$${\ displaystyle k ^ {i} \ sin \ theta ^ {i} = k {\ frac {\ sin \ theta} {M}}.}

Esta es otra forma de escribir la condición sinusoidal de Abbe, que simplemente refleja el principio de incertidumbre clásico para los pares de transformadas de Fourier, es decir, a medida que la extensión espacial de cualquier función se expande (por el factor de ampliación, M ), la extensión espectral se contrae de la misma manera. Factor, M , de modo que el producto de ancho de banda espacial permanezca constante.

La conjetura abc (también conocida como la conjetura Oesterlé-Masser ) es una conjetura en la teoría de los números , propuesta por primera vez por Joseph Oesterlé  ( 1988 ) y David Masser  ( 1985 ). Se afirma en términos de tres números enteros positivos, un, b y c (de ahí el nombre) que son relativamente primos y satisfacen un + b = c . Si d denota el producto de los distintos factores primosde abc, la conjetura esencialmente establece que d no suele ser mucho menor que c . En otras palabras: si a y b se componen de grandes poderes de primos, entonces c no suele ser divisible por grandes poderes de primos. La declaración precisa se da a continuación. La conjetura abc se originó como resultado de los intentos de Oesterlé y Masser de comprender la conjetura de Szpirosobre las curvas elípticas. ^[1] La última conjetura tiene más estructuras geométricas involucradas en su declaración en comparación con la conjetura abc .

La conjetura abc y sus versiones expresan, en forma concentrada, alguna característica fundamental de varios problemas en la geometría diofántica. Una serie de conjeturas y teoremas famosos en la teoría de números seguirían inmediatamente de la conjetura abc o sus versiones. Goldfeld (1996) describió la conjetura abc como "el problema no resuelto más importante en el análisis diofántico ".

Se hicieron varios intentos para probar la conjetura abc, pero hasta ahora ninguno ha sido aceptado por la comunidad matemática, y desde 2019 la conjetura aún no está probada.

Formulaciones [ editar ]

Antes de establecer la conjetura, introducimos la noción del radical de un entero : para un entero positivo n , el radical de n , que se denota rad ( n ), es el producto de los distintos factores primos de n . Por ejemplo

rad (16) = rad (2 ⁴ ) = 2,

rad (17) = 17,

rad (18) = rad (2 ⋅ 3 ² ) = 2 · 3 = 6,

rad (1000000) = rad (2 ⁶ ⋅ 5 ⁶ ) = 2 ⋅ 5 = 10.

Si a , b , yc son coprimos ^[2] enteros positivos tales que a + b = c , resulta que "generalmente" c abc ). La conjetura abc trata de las excepciones. Específicamente, establece que:

Conjetura de ABC. Para cada número real positivo ε , existen solo finamente muchos triples ( a , b , c ) de números enteros positivos de coprime, con a + b = c , de manera que:

{\ displaystyle c> \ operatorname {rad} (abc) ^ {1+ \ varepsilon}.}

Una formulación equivalente establece que:

Conjetura de ABC II. Para cada número real positivo ε , existe una constante K _ε tal que para todos los triples ( a , b , c ) de números enteros positivos de coprime, con a + b = c :

{\ displaystyle c

Una tercera formulación equivalente de la conjetura involucra la calidad q ( a , b , c ) del triple ( a , b , c ), definida como

$${\ displaystyle q (a, b, c) = {\ frac {\ log (c)} {\ log (\ operatorname {rad} (abc))}}.}

Por ejemplo,

q (4, 127, 131) = log (131) / log (rad (4 · 127 · 131)) = log (131) / log (2 · 127 · 131) = 0.46820 ...

q (3, 125, 128) = log (128) / log (rad (3 · 125 · 128)) = log (128) / log (30) = 1.426565 ...

Un triple típico ( a , b , c ) de enteros positivos coprime con a + b = c tendrá c abc ), es decir, q ( a , b , c ) <1 .="" con="" font="" nbsp="" se="" triplica="">q > 1 como en el el segundo ejemplo es bastante especial, consiste en números divisibles por altas potencias de pequeños números primos .

Conjetura de ABC III. Para cada número real positivo ε , existen solo finamente muchos triples ( a , b , c ) de números enteros positivos de coprime con a + b = c , de manera que q ( a , b , c )> 1 + ε .

Si bien se sabe que hay infinitos triples ( a , b , c ) de enteros positivos de coprime con a + b = c , de manera que q ( a , b , c )> 1, la conjetura predice que solo muchos de ellos tienen q > 1.01 o q > 1.001 o incluso q > 1.0001, etc. En particular, si la conjetura es cierta, entonces debe existir un triple ( a , b , c ) que alcance la máxima calidad posible q ( a ,b , c ).

Ejemplos de triples con pequeño radical [ editar ]

La condición de que ε > 0 es necesaria ya que existen infinitos triples a , b , c con rad ( abc ) < c . Por ejemplo, dejar:

{\ displaystyle a = 1, \ quad b = 2 ^ {6n} -1, \ quad c = 2 ^ {6n}, \ qquad n> 1.}

Primero notamos que b es divisible por 9:

$${\ displaystyle b = 2 ^ {6n} -1 = 64 ^ {n} -1 = (64-1) (\ cdots) = 9 \ cdot 7 \ cdot (\ cdots)}

Usando este hecho calculamos:

{\ displaystyle {\ begin {alineado} \ operatorname {rad} (abc) & = \ operatorname {rad} (a) \ operatorname {rad} (b) \ operatorname {rad} (c) \\ & = \ operatorname { rad} (1) \ operatorname {rad} \ left (2 ^ {6n} -1 \ right) \ operatorname {rad} \ left (2 ^ {6n} \ right) \\ & = 2 \ operatorname {rad} \ izquierda (2 ^ {6n} -1 \ derecha) \\ & = 2 \ operatorname {rad} \ izquierda (9 \ cdot {\ tfrac {b} {9}} \ derecha) \\ & \ leqslant 2 \ cdot 3 \ cdot {\ tfrac {b} {9}} \\ & = 2 {\ tfrac {b} {3}} \\ & <{\ tfrac {2} {3}} c \ end {alineado}}}

Al reemplazar el exponente 6 n por otros exponentes, lo que obliga a b a tener factores cuadrados más grandes, la relación entre el radical y c puede hacerse arbitrariamente pequeña. Específicamente, sea p > 2 un primo y considere:

{\ displaystyle a = 1, \ quad b = 2 ^ {p (p-1) n} -1, \ quad c = 2 ^ {p (p-1) n}, \ qquad n> 1.}

Ahora afirmamos que b es divisible por p ² :

{\ displaystyle {\ begin {alineado} b & = 2 ^ {p (p-1) n} -1 \\ & = \ left (2 ^ {p (p-1)} \ right) ^ {n} -1 \\ & = \ left (2 ^ {p (p-1)} - 1 \ right) (\ cdots) \\ & = p ^ {2} \ cdot r (\ cdots) \ end {alineado}}}

El último paso utiliza el hecho de que p ² divide 2 ^p ( p -1) -1. Esto se deduce del pequeño teorema de Fermat , que muestra que, para p > 2, 2 ^p -1 = pk +1 para algún entero k . Elevar ambos lados a la potencia de p muestra que 2 ^p ( p -1) = p ² (...) + 1.

Y ahora con un cálculo similar al anterior tenemos:

{\ displaystyle \ operatorname {rad} (abc) <{\ tfrac {2} {p}} c}

A continuación se presenta una lista de los triples de la más alta calidad (triples con un radical particularmente pequeño en relación a c ); la calidad más alta, 1.6299, fue encontrada por Eric Reyssat ( Lando & Zvonkin 2004 , p. 137) para

a = 2,

b = 3 ¹⁰ · 109 = 6,436,341,

c = 23 ⁵ = 6,436,343,

rad ( abc ) = 15042.