
El estudio de las propiedades estructurales y su optimización así como su dinámica son objeto del análisis de redes.
Análisis de Redes Sociales
Las redes sociales son objeto de estudio particular en diversos campos que van desde la sociología hasta la gestión del conocimiento en las empresas.5 El estudio se centra en la asociación y medida de las relaciones y flujos entre las personas, grupos, organizaciones, computadoras, sitios web, así como cualquier otra entidad de procesamiento de información/conocimiento. Los nodos en la red en este caso son personas y grupos mientras que los enlaces muestran relaciones o flujos entre los nodos.1 El análisis de redes sociales proporciona herramientas6 tanto visuales como matemáticas para el estudio de de las relaciones humanas.
En muchos casos el análisis de redes sociales se fundamenta en el estudio de los agentes en la estructura de la red, para ello se hace un análisis de las medidas de centralidad de los actores de la propia red social con el objetivo de ver las relaciones de poder, de protagonismo, confianza, etc.1 Así como la detección de comunidades, grupos, etc. debido a la existencia de clusteresespecíficos.1
Análisis de Redes de Transporte
Las redes de transporte son objeto de estudio particular en ciertos casos donde se pretende analizar el transporte de bienes y personas entre diversas áreas geográficas. Uno de los objetivos de sus estudio es a veces la mejora y la eficiencia del tráfico. En este análisis los nodos suelen ser las ciudades, los aeropuertos, las estaciones, etc. mientras que los enlaces suelen ser las carreteras, las autovías, etc. Es objeto de estudio del análisis de redes de transporte se centra en las características de capacidad tales como la admisión de elementos de transporte: aviones, coches, etc. la capacidad del flujo de bienes, etc. planificación del transporte.
Teorema de Redes Eléctricas
El estudio de las propiedades de los circuitos eléctricos y el abastecimiento de energía eléctrica a los diversos puntos de distribución. En el estudio se hace uso de ciertos teoremas como el de Thévenin y Norton así como las leyes de Kirchhoff que permiten hacer redes equivalentes más sencillas para que sea posible su estudio simplificado de las mismas.
Postulados básicos
El análisis reticular en sociología comparte con el desarrollado en otras ciencias sociales un cierto número de preocupaciones básicas:
1.- El análisis reticular se encuadra en una sociología estructural: su principal objetivo es la búsqueda de las determinaciones estructurales de la acción humana, y no de las motivaciones individuales o colectivas de los individuos.2.- El concepto de estructura, implícito o explícito, utilizado en las investigaciones reticulares presupone que las estructuras se manifiestan en la forma de los VÍNCULOS ("ties") existentes entre los elementos o NODOS diferenciados que integran un sistema social, siendo estos nodos "actores sociales" o cualquier tipo de entidades sociales significativas (individuos, grupos, organizaciones, clases). Las REDES SOCIALES son pues CONJUNTOS DE VÍNCULOS ENTRE NODOS.3.- Los conjuntos de vínculos entre entidades sociales constituyen los datos básicos del análisis reticular: la estructura buscada se concibe como pautas o regularidades en las formas de vinculación que emergen en los conjuntos relacionales como consecuencia de –un análisis: la estructura de las relaciones no es directamente observable en los datos, que son de naturaleza compleja e incoherente en su apariencia inmediata.4.- El análisis relacional presupone que las características estructurales de las redes de relaciones sociales descubiertas en el curso del análisis determinan los comportamientos de los individuos implicados en ellas.5.- Por ello, el análisis reticular concibe los sistemas sociales como redes de relaciones sociales, más que como conjunto de individuos cuya conducta está regularizada por conjunto de normas y valores interiorizados, por atributos individuales o por meras relaciones diádicas (la interacción de la psicología social). Los VÍNCULOS no son necesariamente diadicos y el análisis reticular considera los VÍNCULOS ENTRE VÍNCULOS como un elemento esencial de la estructura.6.- Así, el análisis reticular de un sistema social es, ante todo, el de un conjunto estructurado de posiciones sociales: el concepto de rol aparece como una variable dependiente de la posición misma y no como la que designa las unidades significativas de los sistemas sociales. En consecuencia, las dimensiones valorativas y normativas de la conducta son, para el análisis reticular, como las demás dimensiones de la motivación, más bien efectos que causa.7.- Los vínculos entre los nodos que definen un retículo social son, en buena parte de las investigaciones concretas realizadas hasta hoy, flujos de información, de bienes o de influencia. Por ello las estructuras sociales descritas diferencian posiciones relativamente a esas dimensiones.
Instrumentos analíticos
Las técnicas de análisis empleadas en las investigaciones reticulares presentan características diferenciales respecto a las técnicas usuales de investigación social. Estas diferencias se derivan del objeto mismo que se analiza
En efecto, las REDES de relaciones sociales son CONJUNTOS DE VÍNCULOS entre entidades y no conjunto de entidades o individuos. Por ello, las técnicas estadísticas usuales no son adecuadas para el análisis reticular, ya que postulan el carácter aleatorio de las relaciones inter-individuales al considerar conjuntos de individuos atomizados, elegidos aleatoriamente por los procedimientos de muestreo
Las técnicas estadísticas usuales conllevan una concepción categorial y distributiva de las estructuras: sus resultados son siempre distribuciones –uni o multivariadas- de atributos individuales. Y cuando se examinan distribuciones de categoría agregadas de atributos tampoco se analizan directamente relaciones sociales, sino sus efectos sobre las variables atributivas.
Además, al desdeñar las vinculaciones concretas entre los individuos, las técnicas usuales de análisis sólo pueden explicar la acción colectiva atribuyendo a las normas interiorizadas un papel causal desmesurado.
Por todo ello, el análisis reticular ha buscado instrumentos heurísticos y de formalización en formas de pensamiento matemático ajenas a la estadística. Primero, en la TEORIA DE GRAFOS, sector de la teoría matemática poco formalizado, muy descriptivo y que se incluye en la topología. Pero después ha encontrado inspiración en teorías algebraicas abstractas como la teoría de semigrupos. Finalmente, la teoría de las categorías y desarrollos topológicos como la teoría de los complejos simpliciales han visto en el análisis de redes sociales un inesperado campo de aplicación y desarrollo.
Una de las dimensiones más interesantes del pensamiento reticular en sociología estriba, precisamente, en el desarrollo de instrumentos matemáticos propios en lugar de la aplicación a su propio campo de conceptos forjados en problemáticas empíricas muy alejadas: así puede concebirse el esfuerzo realizado por la "escuela de Harvard" y, en particular, por los trabajos de FRANCOIS LORRAIN. Características estructurales de las redes Las redes de relaciones sociales se han analizado mediante el uso de conceptos de:
- Centralidad
- "Cliques" o conglomerados
Ambos conceptos están destinados a poner en evidencia singularidades estructurales, puntos de particular significación o conjuntos de puntos asimilables entre ellos. Pero su empleo exige la definición de medidas adecuadas, cuyo desarrollo ha llevado a plantearse con mayor rigor la problemática de las variaciones locales en la densidad relacional. Para resolver el problema se han aplicado conceptos de la teoría de grafos, como entre otros, el de la longitud de los caminos más cortos entre dos puntos.
Existen hoy numerosas definiciones de la centralidad y de su medida, como de las cliques o conglomerados y de la heurística que lleva a su detección. Sin embargo, en el curso de las investigaciones empíricas ha acabado por emerger (LORRAIN y WHITE, 1971) el concepto de equivalencia estructural en las redes: dos individuos o NODOS SON ESTRUCTURALMENTE EQUIVALENTES CUANDO SUS RELACIONES CON TODOS LOS DEMAS PUNTOS SON IDENTICAS.
El concepto de equivalencia estructural permite identificación de todos los nodos equivalentes, constituye, por así decirlo, el esqueleto de la red analizada: se llaman POSICIONES los nodos de una red reducida mediante la aplicación de este concepto de equivalencia estructural. El concepto de equivalencia estructural desarrollado por Lorrain y White se traduce en una metodología de difícil aplicación para redes formadas por números sustanciales de nodos, ya que acude al análisis de categorías para la identificación de las vinculaciones compuestas –vinculaciones entre vinculaciones- de orden N, siendo N el número total de nodos existentes en la red. El análisis de la COMPOSICION de LAS RELACIONES exige un elevado volumen de cálculo, que para redes de 1000 nudos sigue siendo irrealizable a pesar del aumento de capacidad y de velocidad de los ordenadores electrónicos. Por ello se han desarrollado conceptos menos exigentes de equivalencia estructural, como el de los BLOCKMODELS de Breiger, Boormar y White (1976) que desemboco en algoritmos para el análisis de la equivalencia aplicables a redes de centenares de nodos.
No es posible detenerse aquí en un examen de los conceptos y los métodos desarrollados hasta hoy para el análisis de las redes de relaciones sociales: cabe afirmar que las diferentes formalizaciones matemáticas y empíricas son menos significativas en el devenir de esta problemática que su insistencia en definir el objeto de la investigación sociológica como de naturaleza intrínsecamente relacional, desde los datos básicos que se acumulan hasta los resultados de sus análisis.
Antecedentes del análisis de redes
La insistencia en el carácter relacional del objeto de la sociología, como buena parte de los postulados comunes a las investigaciones reticulares contemporáneas tiene antecedentes que llegan hasta los orígenes de la sociología: para muchos sociólogos, se pueden encontrar en DURKHEIM, en SIMMEL, o en el mismo MARX; para los antropólogos, el concepto de red de relaciones sociales se identifica con el objeto mismo de sus investigaciones empíricas, como evidencian los trabajos de NADEL o de BARNES. Los psicosociólogos encuentran en la sociometría de MORENO el indiscutible origen de la problemática del análisis reticular...
Es indudable que el pensamiento estructural en las ciencias sociales está asociado desde sus orígenes a la búsqueda regularidades en las redes de relaciones sociales, que estas regularidades en las formas de relación han sido concebidas como factores causales en la conducta individual o colectiva. No es menos indudable que la componente estructural en el pensamiento sociológico no ha desaparecido en los avatares de una historia en gran parte cíclica. Por ello, la principal novedad del análisis reticular estriba ante todo en la decidida voluntad de construir modelos matemáticos de las propiedades de los espacios reticulares en los que se dibujan las estructuras sociales.
Siendo una voluntad modesta, es esta una contribución de capital importante al desarrollo de la sociología, como lo fue para la física la construcción matemática del espacio continuo y tridimensional en el que se podían definir con rigor las posiciones y los desplazamientos de los cuerpos. El concepto de posición de un punto es indispensable para describir el más simple de los fenómenos de la física clásica: el cambio de posición.
Pero el concepto de posición solo se construye con rigor en física con el cálculo diferencial. La construcción de un concepto de posición en sociología va a requerir construir un espacio con propiedades peculiares respecto al de la física: discreto, discontinuo y relacional, el espacio propio de los sistemas sociales exige una matemática propia y no la mera aplicación de unos instrumentos analíticos desarrolladas para la física, para un espacio continuo o infinito.
apareamiento o conjunto independiente de aristas, también llamado emparejamiento o matching(en inglés), en un grafo es un conjunto de aristas independientes, es decir, sin vértices en común.
Definición
Dado un grafo un apareamiento M en G es un conjunto de aristas no adyacentes entre sí.
Decimos que un vértice está apareado (acoplado saturado) si es incidente con una arista en el apareamiento. En otro caso, el vértice está libre.
Un apareamiento máximo es un apareamiento que contiene el número máximo posible de aristas. Pueden haber muchos apareamientos máximos. El número de apareamiento de un grafo es el tamaño del apareamiento máximo.
Un apareamiento maximal es un apareamiento M de un grafo G con la propiedad de que si alguna arista que no pertenece a M es añadido a M, no será ya un apareamiento. Nótese que todos los apareamiento máximos deben ser maximales, pero no todos los apareamiento maximales deben de ser máximos.
Un apareamiento perfecto es un apareamiento que cubre todos los vértices del grafo. Esto es, cada vértice está saturado bajo el apareamiento. Cada apareamiento perfecto es máximo y maximal.
Dado un apareamiento M
- un camino M-alterno es un camino en el cual sus aristas alternativamente pertenecen y no pertenecen al apareamiento.
- un camino M-incremento es un camino M-alternato que comienza y termina en un vértice libre.
Nótese que un apareamiento es máximo si y sólo si no contiene ningún camino M-incremento.
Apareamientos en grafos bipartitos
Los problemas de apareamiento tienen relación muchas veces con grafos bipartitos. Encontrar un apareamiento máximo bipartito (a menudo llamado cardinalidad máxima de un grafo bipartito) en un grafo bipartito es quizás el problema más simple. El algoritmo de los caminos aumentantes lo encuentra por búsqueda de caminos aumentantes por cada a y añadiéndolo al apareamiento si existe. Como cada camino puede ser encontrado en tiempo , el costo de tiempo es . Todas las aristas con flujo de a constituyen un apareamiento máximo. Una mejora sobre esto es el algoritmo de Hopcroft-Karp, de costo de tiempo .
En un grafo bipartito ponderado, cada arista tiene asociado un valor. Un apareamiento máximo bipartito ponderado está definido como un apareamiento perfecto donde la suma de los valores de sus arcos en el apareamiento tiene un valor maximal. Si el grafo no es completamente bipartito, los arcos ausentes son introducidos con valor cero. Encontrar tal apareamiento es conocido como problema del asignamiento. Para resolverlo se usa la búsqueda del camino mínimo modificado con el algoritmo del camino aumentante. Si usamos el algoritmo de Bellman-Ford, con costo de tiempo . El más especializado es el algoritmo Húngaro que resuelve el problema de asignación con costo de tiempo .
Apareamientos en grafos generales
Existe un algoritmo en tiempo polinomial que es capaz de encontrar un emparejamiento máximo en un grafo que no es bipartito. Este fue desarrollado por Jack Edmonds y fue publicado en un artículo llamado Paths, trees, and flowers en 1965.1 El algoritmo recibe el nombre de Algoritmo de Emparejamiento de Edmonds.
Propiedades
- Para un grafo G con n vértices con un vértice aislado el número de apareamiento + número de aristas de covering = n.2
- Un grafo con n vértices y un apareamiento perfecto tiene un número de apareamiento igual a n/2.
Apareamiento (teoría de grafos)
Definición
Dado un grafo un apareamiento M en G es un conjunto de aristas no adyacentes entre sí.
Decimos que un vértice está apareado si es incidente con una arista en el apareamiento. En otro caso, el vértice está libre.
Un apareamiento máximo es un apareamiento que contiene el número máximo posible de aristas. Pueden haber muchos apareamientos máximos. El número de apareamiento de un grafo es el tamaño del apareamiento máximo.
Un apareamiento maximal es un apareamiento M de un grafo G con la propiedad de que si alguna arista que no pertenece a M es añadido a M, no será ya un apareamiento. Nótese que todos los apareamiento máximos deben ser maximales, pero no todos los apareamiento maximales deben de ser máximos.
Un apareamiento perfecto es un apareamiento que cubre todos los vértices del grafo. Esto es, cada vértice está saturado bajo el apareamiento. Cada apareamiento perfecto es máximo y maximal.
Dado un apareamiento M
- un camino M-alterno es un camino en el cual sus aristas alternativamente pertenecen y no pertenecen al apareamiento.
- un camino M-incremento es un camino M-alternato que comienza y termina en un vértice libre.
Nótese que un apareamiento es máximo si y sólo si no contiene ningún camino M-incremento.
Apareamientos en grafos bipartitos
Los problemas de apareamiento tienen relación muchas veces con grafos bipartitos. Encontrar un apareamiento máximo bipartito en un grafo bipartito es quizás el problema más simple. El algoritmo de los caminos aumentantes lo encuentra por búsqueda de caminos aumentantes por cada a y añadiéndolo al apareamiento si existe. Como cada camino puede ser encontrado en tiempo, el costo de tiempo es. Todas las aristas con flujo de a constituyen un apareamiento máximo. Una mejora sobre esto es el algoritmo de Hopcroft-Karp, de costo de tiempo.
En un grafo bipartito ponderado, cada arista tiene asociado un valor. Un apareamiento máximo bipartito ponderado está definido como un apareamiento perfecto donde la suma de los valores de sus arcos en el apareamiento tiene un valor maximal. Si el grafo no es completamente bipartito, los arcos ausentes son introducidos con valor cero. Encontrar tal apareamiento es conocido como problema del asignamiento. Para resolverlo se usa la búsqueda del camino mínimo modificado con el algoritmo del camino aumentante. Si usamos el algoritmo de Bellman-Ford, con costo de tiempo. El más especializado es el algoritmo Húngaro que resuelve el problema de asignación con costo de tiempo.
Apareamientos en grafos generales
Existe un algoritmo en tiempo polinomial que es capaz de encontrar un emparejamiento máximo en un grafo que no es bipartito. Este fue desarrollado por Jack Edmonds y fue publicado en un artículo llamado Paths, trees, and flowers en 1965. El algoritmo recibe el nombre de Algoritmo de Emparejamiento de Edmonds.

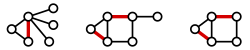
 un apareamiento M en G es un conjunto de aristas no adyacentes entre sí.
un apareamiento M en G es un conjunto de aristas no adyacentes entre sí.
 es quizás el problema más simple. El algoritmo de los caminos aumentantes lo encuentra por búsqueda de caminos aumentantes por cada
es quizás el problema más simple. El algoritmo de los caminos aumentantes lo encuentra por búsqueda de caminos aumentantes por cada  a
a  y añadiéndolo al apareamiento si existe. Como cada camino puede ser encontrado en tiempo
y añadiéndolo al apareamiento si existe. Como cada camino puede ser encontrado en tiempo  , el costo de tiempo es
, el costo de tiempo es  . Todas las aristas con flujo de
. Todas las aristas con flujo de  a
a  .
. . El más especializado es el
. El más especializado es el  .
.
No hay comentarios:
Publicar un comentario