En física, la posición de una partícula indica su localización en el espacio o en el espacio-tiempo. Se representa mediante sistemas de coordenadas.
En mecánica clásica, la posición de una partícula en el espacio se representa como una magnitud vectorial respecto a un sistema de coordenadas de referencia. En relatividad general, la posición no es representable mediante un vector euclidiano, ya que en el espacio-tiempo es curvo en esa teoría, por lo que la posición necesariamente debe representarse mediante un conjunto de coordenadas curvilíneas arbitrarias, que en general no pueden ser interpretadas como las componentes de un vector físico genuino. En mecánica cuántica, la representación de la posición de una partícula es aún más compleja, debido a los efectos de no localidad relacionados con el problema de la medida de la mecánica cuántica.
En general, en un sistema físico o de otro tipo, se utiliza el término posición para referirse al estado físico o situación distinguible que exhibe el sistema. Así es común hablar de la posición del sistema en un diagrama que ilustre variables de estado del sistema.
Posición de un punto P en un sistema de coordenadas cartesianas.
Vector posición en mecánica clásica
En mecánica clásica, debido al carácter euclídeo del espacio, la posición de una partícula se representa mediante el vector de posición o radio vector, usualmente simbolizado con la letra o mediante las coordenadas del punto geométrico del espacio en el que se encuentra la partícula.
La diferencia del vector posición entre dos posiciones distintas recibe el nombre de vector desplazamiento y se le designa por (desplazamiento finito) o por (desplazamiento infinitesimal).
Sistemas de referencia
Podemos representar la posición de una partícula o de un punto del espacio, respecto de un sistema de ejes, mediante las coordenadas cartesianas (x,y,z) del punto, o mediante el vector de posición de dicho punto respecto al origen "O" del sistema de coordenadas (Figura 1). Dicho vector de posición se define como el vector que tiene como origen el punto "O" y como extremo el punto "P", es decir, el vector aplicado en el punto "O" que tiene como componentes las coordenadas cartesianas x, y, z, del punto "P". Escribiremos
siendo los versores asociados a los ejes coordenados respectivos. En general, un sistema de referencia queda definido por un origen y una base vectorial asociada. Si la base vectorial es ortogonal (i.e., si los tres versores que la definen son perpendiculares entre sí), el sistema de referencia también es ortogonal.
Traslación y rotación del sistema de referencia
Merece particular atención considerar el vector de posición cuando cambia por traslación el sistema de referencia, pues entonces cambia el vector de posición del punto P. Entre los vectores de posición del punto P respecto a los sistemas de referencia de origen en O y en O′ existe la relación
y, consecuentemente, las componentes del vector de posición no son invariantes en las traslaciones del sistema de referencia.
De mismo modo, las componentes del vector de posición no son invariantes en las rotaciones del sistema de referencia, transformando sus componentes mediante la correspondiente matriz de rotación.
Derivada temporal del vector de posición
Cuando la partícula permanece en reposo en el sistema de referencia, sus coordenadas no cambian en el transcurso del tiempo y su vector de posición será constante:
Si la posición de una partícula puntual P cambia con el tiempo, en un instante dado se representa por:
En un sistema de referencia fijo, la base coordenada para expresar la posición de vectores tiene la propiedad de permanecer fija, con lo cual el vector velocidad respecto a un sistema inercial puede obtenerse simplemente derivando las componentes del vector de posición respecto al tiempo:
Esto contrasta con el caso de un sistema de referencia móvil, en los que aparecen términos adicionales asociados al movimiento del referencial.
Derivada del vector de posición en referenciales en rotación
Cuando el movimiento de la partícula se describe a un sistema de referencia móvil (x,y,z) en rotación con respecto de un referencial fijo (X,Y,Z) con el que comparte el mismo origen, el vector de posición será el mismo en ambos referenciales y vendrá expresado por:
en el referencial móvil (x,y,z). Puesto que los versores cartesianos (i,j,k)son función del tiempo, al derivar el vector posición con respecto al tiempo aparecerán términos relacionados se obtiene:
siendo la velocidad angular asociada a la rotación del referencial móvil con respecto al referencial fijo.
En términos de la geometría diferencial los términos adicionales tienen que ver con la conexión asociada al sistema de coordenadas o referencia escogido:
Donde:
- son los símbolos de Christoffel que caracterizan la conexión.
- son las componentes de la velocidad.
Posición en mecánica relativista
En la teoría especial de la relatividad el espacio-tiempo de Minkowski tiene geometría pseudoeuclídea pero en lo esencial existe una biyección entre ese espacio y por lo que puede definirse un cuadrivector posición análogo en muchos aspectos al vector posición de la mecánica clásica:
La derivada de este vector respecto al tiempo propio resulta ser la cuadrivelocidad que es el análogo relativista de la velocidad de la mecánica clásica:
Sin embargo en la teoría general de la relatividad las cosas se complican debido a que en ese contexto el espacio-tiempo generalmente es curvo. En ese caso no existe una biyección directa entre el espacio-tiempo y el espacio euclídeo tridimensional y por tanto no resulta posible describir la posición de un punto del espacio-tiempo mediante un vector euclídeo. Aunque como el espacio-tiempo cuatridimensional es localmente difeomórfico con el espacio eclídeo tridimensional, pueden emplearse coordenadas curvilíneas que tienen leyes de transformación tensorial similares a un cuadrivector, aunque las cuatro coordenadas de un punto no pueden ser identificadas con un cuadrivector.
Posición en mecánica cuántica
En mecánica cuántica no-relativista para la mayoría de los sistemas no puede hablarse de la posición de una determinada partícula o incluso de su trayectoria. Esto es una consecuencia del principio de incertidumbre de Heisenberg. En esta teoría las coordenadas intervienen sólo como argumento de la función de onda que describe un sistema, pero en general esas coordenadas no designan la posición de ninguna partícula.
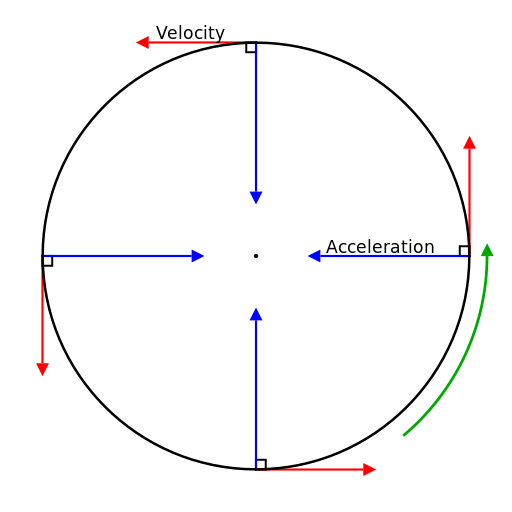
La velocidad es una magnitud física de carácter vectorial que expresa la distancia recorrida de un objeto por unidad de tiempo. Se representa por o . En análisis dimensional sus dimensiones son [L]/[T].1 2 Su unidad en el Sistema Internacional de Unidades es el metro por segundo (símbolo m/s).
En virtud de su carácter vectorial, para definir la velocidad debe considerarse la dirección del desplazamiento y el módulo, el cual se denomina celeridad o rapidez.3
De igual forma que la velocidad es el ritmo o tasa de cambio de la posición por unidad de tiempo, la aceleración es la tasa de cambio de la velocidad por unidad de tiempo y espacio.
Definición de los vectores velocidad media e instantánea.
Historia
Aristóteles estudió los fenómenos físicos sin llegar a conceptualizar una noción de velocidad. En efecto, sus explicaciones (que posteriormente se demostrarían incorrectas) solo describían los fenómenos en palabras, sin usar las matemáticas como herramienta.
Fue Galileo Galilei quien, estudiando el movimiento de los cuerpos en un plano inclinado, llegó a un concepto de velocidad. Lo que hizo fue dividir la distancia recorrida en unidades de tiempo. Esto es, fijó un patrón de una unidad de tiempo, como por ejemplo 1 segundo, y a partir de esto relacionó la distancia recorrida por un cuerpo en cada segundo. De esta manera, Galileo desarrolló el concepto de la velocidad como una variación de la distancia recorrida por unidad de tiempo. A pesar del gran avance de la introducción de esta nueva noción, sus alcances se restringían a los alcances mismos de las matemáticas. Por ejemplo, era relativamente sencillo calcular la velocidad de un móvil que se desplaza a velocidad constante, puesto que en cada segundo recorre distancias iguales. A su vez, también lo era calcular la velocidad de un móvil en aceleración constante, como en un cuerpo en caída libre. Sin embargo, cuando la velocidad del objeto variaba, no había herramienta, en épocas de Galileo, que ayudase a determinar la velocidad instantánea de un objeto.
Fue recién en el siglo XVI cuando, con el desarrollo del cálculo por parte de Isaac Newton y Gottfried Leibniz, se pudo solucionar la cuestión de obtener la velocidad instantánea de un objeto. Esta está determinada por la derivada de la posición del objeto respecto del tiempo. En el lenguaje cotidiano empleamos las palabras rapidez y velocidad de manera indistinta. En física hacemos una distinción entre ellas. De manera muy sencilla, la diferencia es que la velocidad es una rapidez en una dirección determinada. Cuando se dice que un auto viaja a 60 km/hora estamos indicando su rapidez. Pero si se dice que un auto se desplaza a 60 km/h hacia el norte estamos especificando su velocidad y la velocidad nos dice que tan aprisa lo hace y en que dirección.
Las aplicaciones de la velocidad, con el uso de Cálculo, es una herramienta fundamental en Física e Ingeniería, extendiéndose en prácticamente todo estudio donde haya una variación de la posición respecto del tiempo.
Velocidad en mecánica clásica
Velocidad media
La 'velocidad media' o velocidad es el cambio de posición en el tiempo. Se calcula dividiendo el desplazamiento (Δr) entre el tiempo (Δt) empleado en efectuarlo:
(1)
Esta es la definición de la velocidad media entendida como vector (ya que es el resultado de dividir un vector entre un escalar).
Por otra parte, si se considera la distancia recorrida sobre la trayectoria en un intervalo de tiempo dado, tenemos la velocidad media sobre la trayectoria o rapidez media, la cual es una cantidad escalar. La expresión anterior se escribe en la forma:
(2)
La velocidad media sobre la trayectoria también se suele denominar «velocidad media numérica» aunque esta última forma de llamarla no está exenta de ambigüedades.
El módulo de la velocidad media (entendida como vector), en general, es diferente al valor de la velocidad media sobre la trayectoria. Solo serán iguales si la trayectoria es rectilínea y si el móvil solo avanza (en uno u otro sentido) sin retroceder. Por ejemplo, si un objeto recorre una distancia de 10 metros en un lapso de 3 segundos, el módulo de su velocidad media sobre la trayectoria es:
Velocidad instantánea
La velocidad instantánea es un vector tangente a la trayectoria, corresponde a la derivada del vector posición (R) respecto al tiempo.
Permite conocer la velocidad de un móvil que se desplaza sobre una trayectoria cuando el intervalo de tiempo es infinitamente pequeño, siendo entonces el espacio recorrido también muy pequeño, representando un punto de la trayectoria. La velocidad instantánea es siempre tangente a la trayectoria.
donde es un vector (vector de módulo unidad) de dirección tangente a la trayectoria del cuerpo en cuestión y es el vector posición, ya que en el límite los diferenciales de espacio recorrido y posición coinciden.
Celeridad o rapidez
La celeridad o rapidez es una magnitud escalar, a diferencia de la velocidad que es una magnitud vectorial, ya sea velocidad vectorial media, velocidad media sobre la trayectoria, o velocidad instantánea (velocidad en un punto). La celeridad se define como el módulo o norma de la velocidad:
El módulo del vector velocidad instantánea y el valor numérico de la velocidad instantánea sobre la trayectoria son iguales, mientras que la rapidez promedio no necesariamente es igual a la magnitud de la velocidad promedio.
Velocidad relativa
El cálculo de velocidades relativas en mecánica clásica es aditivo y encaja con la intuición común sobre velocidades; de esta propiedad de la aditividad surge el método de la velocidad relativa. La velocidad relativa entre dos observadores A y B es el valor de la velocidad de un observador medida por el otro. Las velocidades relativas medidas por A y B serán iguales en valor absoluto pero de signo contrario. Denotaremos al valor la velocidad relativa de un observador B respecto a otro observador A como .
Dadas dos partículas A y B, cuyas velocidades medidas por un cierto observador son y , la velocidad relativa de B con respecto a A se denota como y viene dada por:
Naturalmente, la velocidad relativa de A con respecto a B se denota como y viene dada por:
de modo que las velocidades relativas y tienen el mismo módulo pero dirección contraria. Aquí E es un sistema inercial de referencia, que puede ser la tierra, p. ej..
Si pasamos Vbe del segundo miembro al primer miembro de la expresión anterior obtenemos: Vae = Vab + Vbe, que nos da la manera de determinar vectorialmente la velocidad de A, en relación a la tierra, cuando se conoce la velocidad de B (en relación a la tierra) y la velocidad relativa de A en relación a B. Esta es una suma vectorial, como se pude observar.
Velocidad angular
La velocidad angular no es propiamente una velocidad en el sentido anteriormente definido sino que es una medida de la rapidez con la que ocurre un movimiento de rotación. Aunque no es propiamente una velocidad una vez conocida la velocidad de un punto de un sólido y la velocidad angular del sólido se puede determinar la velocidad instantánea del resto de puntos del sólido.
Velocidad en mecánica relativista
En mecánica relativista puede definirse la velocidad de manera análoga a como se hace en mecánica clásica sin embargo la velocidad así definida no tiene las mismas propiedades que su análogo clásico:
- En primer lugar la velocidad convencional medida por diferentes observadores, aun inerciales, no tiene una ley de transformación sencilla (de hecho la velocidad no es ampliable a un cuadrivector de manera trivial).
- En segundo lugar, el momento lineal y la velocidad en mecánica relativista no son proporcionales, por esa razón se considera conveniente en los cálculos substituir la velocidad convencional por la cuadrivelocidad, cuyas componentes espaciales coinciden con la velocidad para velocidades pequeñas comparadas con la luz, siendo sus componentes en el caso general:
Además esta cuadrivelocidad tiene propiedades de transformación adecuadamente covariantes y es proporcional al cuadrimomento lineal.
En mecánica relativista la velocidad relativa no es aditiva. Eso significa que si consideramos dos observadores, A y B, moviéndose sobre una misma recta a velocidades diferentes , respecto de un tercer observador O, sucede que:
Siendo la velocidad de B medida por A y la velocidad de A medida por B. Esto sucede porque tanto la medida de velocidades, como el transcurso del tiempo para los observadores A y B no es el mismo debido a que tienen diferentes velocidades, y como es sabido el paso del tiempo depende de la velocidad de un sistema en relación a la velocidad de la luz. Cuando se tiene en cuenta esto, resulta que el cálculo de velocidades relativas no es aditiva. A diferencia de lo que sucede en la mecánica clásica, donde el paso del tiempo es idéntico para todos los observadores con independencia de su estado de movimiento. Otra forma de verlo es la siguiente: si las velocidades relativas fuera simplemente aditiva en relatividad llegaríamos a contradicciones. Para verlo, consideremos un objeto pequeño que se mueve respecto a otro mayor a una velocidad superior a la mitad de la luz. Y consideremos que ese otro objeto mayor se moviera a más de la velocidad de la luz respecto a un observador fijo. La aditividad implicaría que el objeto pequeño se movería a una velocidad superior a la de la luz respecto al observador fijo, pero eso no es posible porque todos los objetos materiales convencionales tienen velocidades inferiores a la de luz. Sin embargo, aunque las velocidades no son aditivas en relatividad, para velocidades pequeñas comparadas con la velocidad de la luz, las desigualdades se cumplen de modo aproximado, es decir:
Siendo inadecuada esta aproximación para valores de las velocidades no despreciables frente a la velocidad de la luz.
Velocidad en mecánica cuántica
En mecánica cuántica no relativista el estado de una partícula se describe mediante una función de onda que satisface la ecuación de Schrödinger. La velocidad de propagación media de la partícula viene dado por la expresión:
Obviamente la velocidad solo será diferente de cero cuando la función de onda es compleja, siendo idénticamente nula la velocidad de los estados ligados estacionarios, cuya función de onda es real. Esto último se debe a que los estados estacionarios representan estados que no varían con el tiempo y por tanto no se propagan.
En mecánica cuántica relativista se postula que por ejemplo un electrón podría tener junto con una velocidad media macroscópica (medida entre dos instantes diferentes) un movimiento de agitación u oscilación muy rápida adicional conocido como Zitterbewegung, de acuerdo con esa interpretación adicional no existe una relación entre el momento de la partícula y la velocidad asignable a dicho movimiento.
Unidades de velocidad
- Sistema Internacional de Unidades (SI)
- Metro por segundo (m/s), unidad de velocidad del SI (1 m/s = 3,6 km/h).
- Sistema Métrico antiguo
- Kilómetro por hora (km/h) (muy habitual en los medios de transporte)Nota 1
- Kilómetro por segundo (km/s)
- Sistema Cegesimal de Unidades
- Centímetro por segundo (cm/s) unidad de velocidad del sistema cegesimal
- Sistema Cexagesimal de Unidades
- También llamado sistema CXGS. Minutos por segundo (min/s) unidad de velocidad del sistema sexagecimal.
- Sistema Anglosajón de Unidades
- Pie por segundo (ft/s), unidad de velocidad del sistema inglés
- Milla por hora (mph) (uso habitual)
- Milla por segundo (mps) (uso coloquial)
- Navegación marítima y Navegación aérea
- El nudo es una unidad de medida de velocidad, utilizada en navegación marítima y aérea, equivalente a la milla náutica por hora (la longitud de la milla naútica es de 1852 metros; la longitud de la milla terrestre —statute mile— es de 1609,344 metros).
- Aeronáutica
- El número Mach es una medida de velocidad relativa que se define como el cociente entre la velocidad de un objeto y la velocidad del sonido en el medio en que se mueve dicho objeto. Es un número adimensional típicamente usado para describir la velocidad de los aviones. Mach 1 equivale a la velocidad del sonido, Mach 2 es dos veces la velocidad del sonido,y así sucesivamente. La velocidad del sonido en el aire es de 340 m/s (1224 km/h).
- Unidades de Planck (Unidades naturales)
- El valor de la velocidad de la luz en el vacío = 299 792 458 m/s (aproximadamente 300 000 km/s).







 o mediante las
o mediante las  (desplazamiento finito) o por
(desplazamiento finito) o por  (desplazamiento infinitesimal).
(desplazamiento infinitesimal).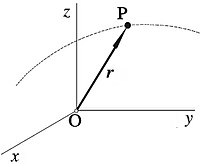

 los
los 








 la
la 
 son los
son los  son las componentes de la velocidad.
son las componentes de la velocidad. por lo que puede definirse un cuadrivector posición análogo en muchos aspectos al
por lo que puede definirse un cuadrivector posición análogo en muchos aspectos al 

 o
o  . En
. En 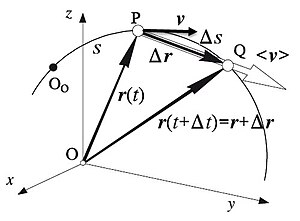





 es un vector (
es un vector (
 .
. y
y  , la velocidad relativa de B con respecto a A se denota como
, la velocidad relativa de B con respecto a A se denota como 
 y viene dada por:
y viene dada por:

 , respecto de un tercer observador O, sucede que:
, respecto de un tercer observador O, sucede que:
 de B medida por A y
de B medida por A y  la velocidad de A medida por B. Esto sucede porque tanto la medida de velocidades, como el transcurso del tiempo para los observadores A y B no es el mismo debido a que tienen diferentes velocidades, y como es sabido el paso del tiempo depende de la velocidad de un sistema en relación a la
la velocidad de A medida por B. Esto sucede porque tanto la medida de velocidades, como el transcurso del tiempo para los observadores A y B no es el mismo debido a que tienen diferentes velocidades, y como es sabido el paso del tiempo depende de la velocidad de un sistema en relación a la 
 que satisface la
que satisface la 
No hay comentarios:
Publicar un comentario