Fisioquímica

geometría molecular

La geometría molecular o estructura molecular se refiere a la disposición tridimensional de los átomos que constituyen una molécula. Determina muchas de las propiedades de las moléculas, reactividad, polaridad, fase, color, magnetismo, actividad biológica, etc. Actualmente, el principal modelo Teoría de Repulsión de Pares de Electrones de Valencia (TRPEV), empleada internacionalmente por su gran predictibilidad.

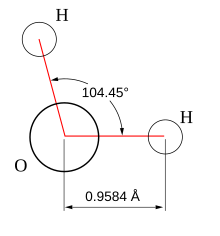
Geometría de la molécula de agua.

Determinación de la geometría molecular

Las geometrías moleculares se determinan mejor cuando las muestras están próximas al cero absoluto porque a temperaturas más altas las moléculas presentarán un movimiento rotacional considerable. En el estado sólido la geometría molecular puede ser medida por Difracción de rayos X. Las geometrías se pueden calcular por procedimientos mecánico cuánticos ab initio o por métodos semiempíricos de modelamiento molecular.

La posición de cada átomo se determina por la naturaleza de los enlaces químicos con los que se conecta a sus átomos vecinos. La geometría molecular puede describirse por las posiciones de estos átomos en el espacio, mencionando la longitud de enlace de dos átomos unidos, ángulo de enlace de tres átomos conectados y ángulo de torsión de tres enlaces consecutivos.

Movimiento atómico

Dado que el movimiento de los átomos en una molécula está determinado por la mecánica cuántica, uno debe definir el "movimiento" de una manera cuántica.

Los movimientos cuánticos (externos) de traslación y rotación cambian fuertemente la geometría molecular. (En algún grado la rotación influye en la geometría por medio de la fuerza de Coriolis y la distorsión centrífuga, pero son despreciables en la presente discusión).

Un tercer tipo de movimiento es la vibración , un movimiento interno de los átomos en una molécula. Las vibraciones moleculares son armónicas (al menos en una primera aproximación), lo que significa que los átomos oscilan en torno a su posición de equilibrio, incluso a la temperatura del cero absoluto. En el cero absoluto todos los átomos están en su estado vibracional basal y muestran movimiento mecánico cuántico de punto cero, esto es, la función de onda de un modo vibracional simple no es un pico agudo, sino un exponencial de ancho finito. A temperaturas mayores, los modos vibracionales pueden ser excitados térmicamente (en un interpretación clásica, esto se expresa al enunciar que "las moléculas vibrarán más rápido"), pero siempre oscilan alrededor de una geometría reconocible para la molécula.

Para tener una comprensión más clara de la probabilidad de que la vibración de una molécula pueda ser térmicamente excitada, se inspecciona el factor de Boltzmann ${\displaystyle \exp \left(-{\frac {\Delta E}{kT}}\right)}$, donde ${\displaystyle \Delta E}$ es la energía de excitación del modo vibracional, ${\displaystyle k}$ es la constante de Boltzmann y ${\displaystyle T}$ es la temperatura absoluta. A 298K (25 °C), unos valores típicos del factor de Boltzmann son: ΔE = 500 cm^-1 --> 0.089; ΔE = 1000 cm^-1 --> 0.008; ΔE = 1500 cm^-1 --> 7 10^-4. Esto es, si la energía de excitación es 500 cm^-1, aproximadamente el 9% de las moléculas están térmicamente excitadas a temperatura ambiente. La menor energía vibracional de excitación es el modo de flexión (aproximadamente 1600 cm^-1). En consecuencia, a temperatura ambiente menos del 0,07% de todas las moléculas de una cantidad dada de agua vibrarán más rápido que en el cero absoluto.

Como se mencionó anteriormente, la rotación influye fuertemente sobre la geometría molecular. Pero, como movimiento mecánico cuántico, se excita a bajas temperaturas (comparada con la vibración). Desde un punto de vista clásico, puede decirse que más moléculas rotan más rápidamente a temperatura ambiente, esto es que tienen mayor velocidad angular y momentum angular. En lenguaje de mecánica cuántica: más "eigenstates" de alto momentum angular son poblados térmicamente al aumentar la temperatura. Las energías de excitación rotacionales típicas están en el orden de unos pocos cm^-1.

Los resultados de muchos experimentos espectroscópicos están ensanchados porque involucran una media de varios estados rotacionales. Frecuentemente es difícil obtener las geometrías a partir de los espectros a altas temperaturas, porque el número de estados rotacionales rastreados en el experimento aumenta al incrementarse la temperatura. En consecuencia, muchas observaciones espectroscópicas sólo se puede esperar que conduzcan a geometrías moleculares confiables a temperaturas cercanas al cero absoluto.

Enlaces Atómicos

Por definición, los átomos en las moléculas suelen estar unidos unos a otros con enlaces covalentes, que pueden ser simples, dobles o triples, donde un "enlace" es un par de electrones compartidos entre átomos vecinos. Otro método de unión entre átomos se denomina enlace iónico en el que intervienen cationes positivos y anionesnegativos, sin que se formen moléculas sino redes iónicas.

La geometría molecular puede ser especificada en términos de longitud de enlace, ángulo de enlace y ángulo torsional. La longitud de enlace está definida como la distancia media entre los centros de dos átomos enlazados en una molécula dada. Un ángulo de enlace es el ángulo formado por tres átomos enlazados consecutivamente. Para cuatro átomos unidos consecutivamente en una cadena línea, el ángulo torsional es el ángulo entre el plano formado por los tres primeros átomos y el plano formado por los tres últimos átomos.

Isómeros

Los isómeros son tipos de moléculas que comparten la misma fórmula química, pero que tienen diferentes geometrías, resultando en propiedades muy distintas:

• Una sustancia "pura" está compuesta de sólo un tipo de isómero de una molécula (todas tienen la misma estructura geométrica).
• Los isómeros estructurales tienen la misma fórmula química, pero diferente ordenamiento físico, frecuentemente formando geometrías moleculares alternas con propiedades muy diferentes. Los átomos no están enlazados (conectados) en el mismo orden.
• Los isómeros funcionales son una clase especial de isómeros estructurales, donde ciertos grupos de átomos exhiben un tipo especial de comportamiento, como es un éter o un alcohol.
• Los estereoisómeros pueden tener muchas propiedades físicoquímicas idénticas y, al mismo tiempo, actividad biológica muy diferente. Esto se debe a que poseen la quiralidad que es muy común en los sistemas vivientes. Una manifestación de esta quiralidad es su habilidad para hacer rotar la luz polarizada en direcciones diferentes.
• Protein folding, que concierne a la compleja geometría y diferentes isómeros que las proteínas pueden tener.

La geometría molecular se representa en una pirámide en la cual en la punta inicial hay una molécula de oxígeno con carga negativa, quedando en las otras dos puntas dos moléculas de hidrógeno con carga positiva, que son separadas por un ángulo de 104.5º; el enlace que une los hidrógenos con el oxígeno se llama enlace covalente, y también existe un enlace que une a otra pirámide idéntica a la anteriormente nombrada llamado enlace puente hidrógeno.

Tipos de estructura molecular

Tipo de molécula	Forma	Disposición electrónica†	Geometría‡	Ejemplos
AX1En	Molécula diatómica			HF, O2, CO
AX2E0	Lineal			BeCl2, HgCl2, CO2, PbCl2
AX2E1	Angular			NO2−, SO2, O3
AX2E2	Angular forma "V"		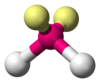	H2O, OF2, SCl2
AX2E3	Lineal			XeF2, I3−
AX3E0	Trigonal plana			BF3, CO32−, NO3−, SO3
AX3E1	Tetraedro piramidal			NH3, PCl3
AX3E2	Forma de T			ClF3, BrF3
AX4E0	Tetraédrica		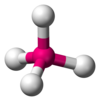	CH4, PO43−, SO42−, ClO4−
AX4E1	Balancín			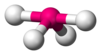SF4
AX4E2	Cuadrada plana			XeF4
AX5E0	Bipirámide trigonal			PCl5
AX5E1	Pirámide cuadrangular		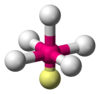	ClF5, BrF5
AX6E0	Octaédrica		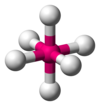	SF6
AX6E1	Pirámide pentagonal			XeOF— 5, IOF2- 51
AX7E0	Bipirámide pentagonal			IF7

† Disposición electrónica incluyendo los pares no enlazantes (mostrados en amarillo) ‡ Geometría observada (excluyendo los pares no enlazantes)

La geometría tridimensional de las moléculas está determinada por la orientación relativa de sus enlaces covalentes. En 1957 el químico canadiense Ron Gillespie basándose en trabajos previos de Nyholm desarrolló una herramienta muy simple y sólida para predecir la geometría (forma) de las moléculas.
La teoría por él desarrollada recibe el nombre Teoría de Repulsión de los Pares de Electrones de Valencia (TRPEV) y se basa en el simple argumento de que los grupos de electrones se repelerán unos con otros y la forma que adopta la molécula será aquella en la que la repulsión entre los grupos de electrones sea mínima.

Para la TRPEV grupos de electrones pueden ser:

• un simple enlace
• un doble enlace
• un triple enlace
• un par de electrones no enlazante

Para predecir la geometría de una molécula necesitamos conocer solamente cuantos grupos de electrones están asociados al átomo central para lo cual debemos escribir la fórmula de Lewis de la molécula.
Luego simplemente nos preguntamos como los grupos de electrones se distribuirán espacialmente de modo que la repulsión entre ellos sea mínima.
Es importante recordar que la geometría de la molécula quedará determinada solamente por la distribución espacial de los enlaces presentes y no por la posición de los pares electrónicos no enlazantes, los que si deberán ser tenidos en cuenta en el momento de determinar la disposición espacial de todos los grupos electrónicos, sean enlaces o no.
Por ejemplo la molécula de H₂S tiene la siguiente fórmula de Lewis: En ella podemos identificar 4 grupos de electrones: dos enlaces simples y dos pares de electrones no enlazantes.Para minimizar las repulsiones entre ellos adoptarán una geometría tetraédrica, colocándose cada grupo en el vértice de un tetraedro que tiene como centro al átomo de azufre. Sin embargo a la hora de determinar la geometría de la molécula, la misma sólo queda determinada por la distribución de los enlaces, por lo que la geometría del H₂S será angular.
Note que el ángulo HSH es menor que 109.5°, el ángulo de un tetraedro regular. Esto se debe a la mayor repulsión generada por el mayor volumen de los pares de electrones no enlazantes.

En la tabla se muestran las distintas geometrías que adoptan las moléculas dependiendo de la cantidad de grupos elctrónicos y enlaces que presentan. 

Total átomos + pares no
enlazantes alrededor
del átomo central Atomos Pares no enlazantes Geometría Ejemplos 2 2 0 Lineal CO₂ 3 3
2 0
1 Trigonal plana
Angular BCl₃
SO₂ 4 4
3
2 0
1
2 Tetraédrica
Pirámide trigonal
Angular SiF₄
PH₃
H₂S 5 5
4
3
2 0
1
2
3 Bipirámide trigonal
Balancín
Forma "T"
Lineal PF₅
SCl₄
IF₃
XeF₂ 6 6
5
4 0
1
2 Octaédrica
Pirámide b.cuadrada
Cuadrada plana SiF₆^-2
IF₅
ICl₄^-