AMIGOS PARA SIEMPRE: Algoritmos

El algoritmo de Dijkstra, también llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de los vértices en un grafo con pesos en cada arista. Su nombre se refiere a Edsger Dijkstra, quien lo describió por primera vez en 1959.

La idea subyacente en este algoritmo consiste en ir explorando todos los caminos más cortos que parten del vértice origen y que llevan a todos los demás vértices; cuando se obtiene el camino más corto desde el vértice origen, al resto de vértices que componen el grafo, el algoritmo se detiene. El algoritmo es una especialización de la búsqueda de costo uniforme, y como tal, no funciona en grafos con aristas de coste negativo (al elegir siempre el nodo con distancia menor, pueden quedar excluidos de la búsqueda nodos que en próximas iteraciones bajarían el costo general del camino al pasar por una arista con costo negativo).

Una de sus aplicaciones más importantes reside en el campo de la telemática, gracias a el, podemos resolver grafos con muchos nodos, los cuales serian muy complicados de hacer sin dicho algoritmo, encontrando así las rutas más cortas entre un origen y todos los destinos en una red.

Algoritmo de Dijkstra
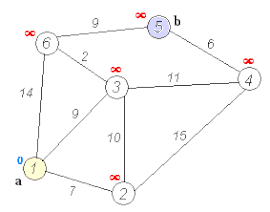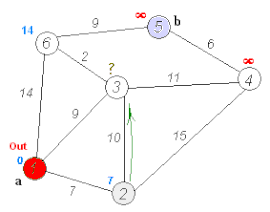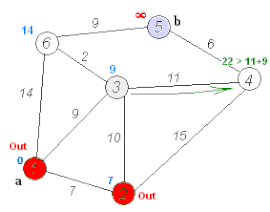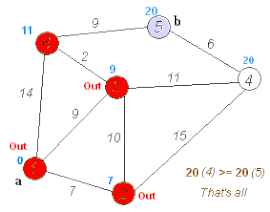Ejecución del algoritmo de Dijkstra
Tipo	Algoritmo de búsqueda
Problema que resuelve	Problema del camino más corto
Estructura de datos	Grafo
Creador	Edsger Dijkstra
Fecha	1959
Clase de complejidad	P
Tiempo de ejecución
Peor caso	$O(\|E\|+\|V\|\log \|V\|)\,$

Algoritmo

Teniendo un grafo dirigido ponderado de N nodos no aislados, sea x el nodo inicial, un vector D de tamaño N guardará al final del algoritmo las distancias desde x al resto de los nodos.

Inicializar todas las distancias en D con un valor infinito relativo ya que son desconocidas al principio, exceptuando la de x que se debe colocar en 0 debido a que la distancia de x a x sería 0.
Sea a = x (tomamos a como nodo actual).
Recorremos todos los nodos adyacentes de a, excepto los nodos marcados, llamaremos a estos nodos no marcados v_i.
Para el nodo actual, calculamos la distancia tentativa desde dicho nodo a sus vecinos con la siguiente fórmula: dt(v_i) = D_a + d(a,v_i). Es decir, la distancia tentativa del nodo ‘v_i’ es la distancia que actualmente tiene el nodo en el vector D más la distancia desde dicho el nodo ‘a’ (el actual) al nodo v_i. Si la distancia tentativa es menor que la distancia almacenada en el vector, actualizamos el vector con esta distancia tentativa. Es decir: Si dt(v_i) < D_vi → D_vi = dt(v_i)
Marcamos como completo el nodo a.
Tomamos como próximo nodo actual el de menor valor en D (puede hacerse almacenando los valores en una cola de prioridad) y volvemos al paso 3 mientras existan nodos no marcados.

Una vez terminado al algoritmo, D estará completamente lleno.

Complejidad

Orden de complejidad del algoritmo: O(|V|²+|A|) = O(|V|²) sin utilizar cola de prioridad, O((|A|+|V|) log |V|) = O(|A| log |V|) utilizando cola de prioridad (por ejemplo un montículo). Por otro lado, si se utiliza un Montículo de Fibonacci, sería O(|V| log |V|+|A|).

Podemos estimar la complejidad computacional del algoritmo de Dijkstra (en términos de sumas y comparaciones). El algoritmo realiza a lo más n-1 iteraciones, ya que en cada iteración se añade un vértice al conjunto distinguido. Para estimar el número total de operaciones basta estimar las que se llevan a cabo en cada iteración. Podemos identificar el vértice con la menor etiqueta entre los que no están en S_krealizando n-1 comparaciones o menos. Después hacemos una suma y una comparación para actualizar la etiqueta de cada uno de los vértices que no están en S_k. Por tanto, en cada iteración se realizan a lo sumo 2(n-1) operaciones, ya que no puede haber más de n-1 etiquetas por actualizar en cada iteración. Como no se realizan más de n-1 iteraciones, cada una de las cuales supone a lo más 2(n-1) operaciones, llegamos al siguiente teorema.

TEOREMA: El Algoritmo de Dijkstra realiza O(n²) operaciones (sumas y comparaciones) para determinar la longitud del camino más corto entre dos vértices de un grafo ponderado simple, conexo y no dirigido con n vértices.

Pseudocódigo

Estructura de datos auxiliar: Q = Estructura de datos Cola de prioridad (se puede implementar con un montículo)

   DIJKSTRA (Grafo G, nodo_fuente s)       
       para u ∈ V[G] hacer
           distancia[u] = INFINITO
           padre[u] = NULL
           visto[u] = false
       distancia[s] = 0
       adicionar (cola, (s, distancia[s]))
       mientras que cola no es vacía hacer
           u = extraer_mínimo(cola)
           visto[u] = true
           para todos v ∈ adyacencia[u] hacer
               si no visto[v] y distancia[v] > distancia[u] + peso (u, v) hacer
                   distancia[v] = distancia[u] + peso (u, v)
                   padre[v] = u
                   adicionar(cola,(v, distancia[v]))

Otra versión en pseudocódigo sin cola de prioridad

función Dijkstra (Grafo G, nodo_salida s)
  //Usaremos un vector para guardar las distancias del nodo salida al resto
  entero distancia[n] 
  //Inicializamos el vector con distancias iniciales
  booleano visto[n] 
  //vector de boleanos para controlar los vértices de los que ya tenemos la distancia mínima
  para cada w ∈ V[G] hacer
     Si (no existe arista entre s y w) entonces
         distancia[w] = Infinito //puedes marcar la casilla con un -1 por ejemplo
     Si_no
         distancia[w] = peso (s, w)
     fin si 
  fin para
  distancia[s] = 0
  visto[s] = cierto
  //n es el número de vértices que tiene el Grafo
  mientras que (no_estén_vistos_todos) hacer 
     vértice = coger_el_mínimo_del_vector distancia y que no esté visto;
     visto[vértice] = cierto;
     para cada w ∈ sucesores (G, vértice) hacer
         si distancia[w]>distancia[vértice]+peso (vértice, w) entonces
            distancia[w] = distancia[vértice]+peso (vértice, w)
         fin si
     fin para 
  fin mientras
fin función.

Al final tenemos en el vector distancia en cada posición la distancia mínima del vértice salida a otro vértice cualquiera.

Otra versión en C del Algoritmo de Dijkstra

#define MAX_NODES 1024 /* número máximo de nodos */
#define INFINITY 1000000000 /* un número mayor que cualquier ruta máxima */
int n, dist[MAX_NODES][MAX_NODES]; /* dist[i][ j] es la distancia de i a j */
void shortest_path(int s, int t, int path[])
{ struct state { /* la ruta en la que se está trabajando */
int predecessor; /* nodo previo */
int length; /* longitud del origen a este nodo */
enum {permanent, tentative} label; /* estado de la etiqueta */
} state[MAX_NODES];
int i, k, min;
struct state *p;
for (p = &state[0]; p < &state[n]; p++) { /* estado de inicialización*/
p->predecessor = -1;
p->length = INFINITY;
p->label = tentative;
}
state[t].length = 0; state[t].label = permanent;
k = t; /* k es el nodo de trabajo inicial */
do{ /* ¿hay una ruta mejor desde k? */
for (i = 0; i < n; i++) /* este grafo tiene n nodos */
if (dist[k][i] != 0 && state[i].label == tentative) {
if (state[k].length + dist[k][i] < state[i].length) {
state[i].predecessor = k;
state[i].length = state[k].length + dist[k][i];
}
}
/* Encuentra el nodo etiquetado tentativamente con la etiqueta menor. */
k = 0; min = INFINITY;
for (i = 0; i < n; i++)
if (state[i].label == tentative && state[i].length < min) {
min = state[i].length;
k = i;
}
state[k].label = permanent;
} while (k != s);
/* Copia la ruta en el arreglo de salida. */
i = 0; k = s;
do {path[i++] = k; k = state[k].predecessor; } while (k >= 0);


La Fórmula del área de Gauss, Fórmula de la Lazada o Algoritmo de la Lazada, es un algoritmo matemático usado para calcular el área de un polígono simple cuyos vértices están descritos como pares de coordenadas en el plano.¹ ²

Es conocido como fórmula de la lazada debido al constante cruce de productos de las correspondientes coordenadas de cada par de vértices, similar al atar una lazada.¹ También recibe el nombre de Fórmula del área de Gauss en honor a Carl Friedrich Gauss. Tiene múltiples aplicaciones en agrimensura e ingeniería de montes entre otras áreas.



El cruce de productos de coordenadas empleado en esta fórmula.




Formulación

La fórmula puede representarse mediante la expresión:
 ${\begin{aligned}\mathbf {A} &={1 \over 2}{\Big |}\sum _{i=1}^{n-1}x_{i}y_{i+1}+x_{n}y_{1}-\sum _{i=1}^{n-1}x_{i+1}y_{i}-x_{1}y_{n}{\Big |}\\&={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+\cdots +x_{n-1}y_{n}+x_{n}y_{1}-x_{2}y_{1}-x_{3}y_{2}-\cdots -x_{n}y_{n-1}-x_{1}y_{n}|\\\end{aligned}}$ 

donde

A es el área del polígono,
n es el número de lados del polígono, y
(x_i, y_i), i = 1, 2,..., n son los vértices del polígono.


de forma alternativa:³ ⁵ ⁶
 $\mathbf {A} ={1 \over 2}{\Big |}\sum _{i=1}^{n}x_{i}(y_{i+1}-y_{i-1}){\Big |}={1 \over 2}{\Big |}\sum _{i=1}^{n}y_{i}(x_{i+1}-x_{i-1}){\Big |}={1 \over 2}{\Big |}\sum _{i=1}^{n}x_{i}y_{i+1}-x_{i+1}y_{i}{\Big |}={1 \over 2}{\Big |}\sum _{i=1}^{n}\det {\begin{pmatrix}x_{i}&x_{i+1}\\y_{i}&y_{i+1}\end{pmatrix}}{\Big |}$ 

donde, al tratarse de un polígono cíclico x_n+1 = x₁ y x_n = x₀, al igual que y_n+1 = y₁ y y_n = y₀.

Si los vértices del polígono están listados de forma secuencial con sentido antihorario, entonces el determinante anterior es positivo, y el operador de valor absoluto puede ser omitido;⁴ Si los vértices están listados con sentido horario, el determinante será siempre negativo. Esto es debido a que la fórmula puede ser vista como un caso especial del Teorema de Green.

(N+1)XN

------------

2

Ejemplos

El usuario debe conocer las coordenadas de los vértices del polígono en un plano cartesiano. Por ejemplo, dado el triángulo con coordenadas {(2, 1), (4, 5), (7, 8)}. Tome la primera coordenada x y multiplíquela por la segunda coordenada y, luego tome la segunda coordenada x y multiplíquela por la tercera coordenada y, y repita hasta hacerlo para todos los vértices. Esto puede definirse mediante la siguiente fórmula:⁷
 $\mathbf {A} _{\text{tri.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|$ 

donde x_i y y_i representan la respectivas coordenadas. Esta fórmula es la expansión de la formulación anterior para el caso n = 3. Uno puede encontrar que el área del triángulo es igual a la mitad del valor absoluto de 10 + 32 + 7 − 4 − 35 − 16, que es igual a 3. El número de variables depende del número de lados del polígono. Por ejemplo, un pentágono definiría coordenadas hasta x₅ y y₅:
 $\mathbf {A} _{\text{pent.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|$ 

Un ejemplo más complejo

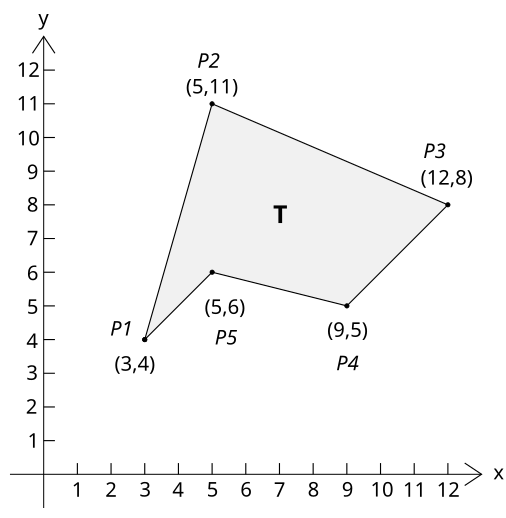
Considere el polígono definido por los vértices (3,4), (5,11), (12,8), (9,5), and (5,6), ilustrado en el siguiente diagrama:



El área del polígono será:
 ${\begin{aligned}\mathbf {A} &={1 \over 2}|3\times 11+5\times 8+12\times 5+9\times 6+5\times 4\\&{}\qquad {}-4\times 5-11\times 12-8\times 9-5\times 5-6\times 3|\\[10pt]&={60 \over 2}=30\end{aligned}}$ 

Explicación del nombre

La razón por la que esta fórmula es llamada fórmula de la lazada es debido a un método común para evaluarla empleando matrices. Por ejemplo, dado el triángulo con vértices (2,4), (3,−8), y (1,2), es posible construir la siguiente matriz apilando las coordenadas y repitiendo el primer vértice al final de la matriz.⁸

 ${\begin{bmatrix}2&4\\3&-8\\1&2\\2&4\end{bmatrix}}$ 


Ahora, dibuje diagonales hacía abajo y a la derecha...
  

y multiplique cada par de números conectados por un trazo, y luego sume todos los productos: (2 × −8) + (3 × 2) + (1 × 4) = −6.

Repita lo mismo con trazos diagonales hacía abajo y la izquierda...
  

obteniendo (4 × 3) + (−8 × 1) + (2 × 2) = 8.

Finalmente, calcule la diferencia entre ambos números y tome su valor absoluto: |−6 − 8| = 14. Dividiendo entre dos, obtendrá el área del triángulo: 7. Organizar los números de esta forma hace más sencillo recordar y evaluar la fórmula. Tras dibujar todos los trazos, la matriz se asemeja al cordón de una zapatilla.