AMIGOS PARA SIEMPRE: Algoritmos

algoritmos de búsquedas de raíces

método de la secante es un método para encontrar los ceros de una función de forma iterativa.

Es una variación del método de Newton-Raphson donde en vez de calcular la derivada de la función en el punto de estudio, teniendo en mente la definición de derivada, se aproxima la pendiente a la recta que une la función evaluada en el punto de estudio y en el punto de la iteración anterior. Este método es de especial interés cuando el coste computacional de derivar la función de estudio y evaluarla es demasiado elevado, por lo que el método de Newton no resulta atractivo.

En otras palabras, el método de la secante es un algoritmo de la raíz de investigación que utiliza una serie de raíces de las líneas secantes para aproximar mejor la raíz de una función f. El método de la secante se puede considerar como una aproximación en diferencias finitas del método de Newton-Raphson. Sin embargo, este método fue desarrollado independientemente de este último.

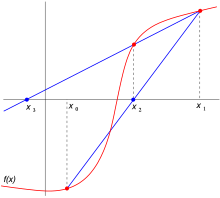
Dos primeras iteraciones del método de la secante.

El método

El método se define por la relación de recurrencia:

x_{n+1}=x_{n}-{\frac {x_{n}-x_{n-1}}{f(x_{n-1}-f(x_{n}))}}f(x_{n}).

Como se puede ver, este método necesitará dos aproximaciones iniciales de la raíz para poder inducir una pendiente inicial.

Derivación del método

El método se basa en obtener la ecuación de la recta que pasa por los puntos (x_n−1, f(x_n−1)) y (x_n, f(x_n)). A dicha recta se le llama secante por cortar la gráfica de la función. En la imagen de arriba a la derecha se toman los puntos iniciales x₀ y x₁, se construye una línea por los puntos (x₀, f(x₀)) y (x₁, f(x₁)). En forma punto-pendiente, esta línea tiene la ecuación mostrada anteriormente. Posteriormente se escoge como siguiente elemento de la relación de recurrencia, x_n+1, la intersección de la recta secante con el eje de abscisas obteniendo la fórmula, y un nuevo valor. Seguimos este proceso, hasta llegar a un nivel suficientemente alto de precisión (una diferencia lo suficientemente pequeñas entre x_n y x_n-1).

Convergencia

El orden de convergencia de este método, en un punto cercano a la solución, es

\varphi

donde

\varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1,618

es el número áureo, por lo que se trata de una convergencia superlineal inferior a la del método de Newton-Raphson. En caso de que la aproximación inicial sea demasiado lejana o la raíz no sea simple, este método no asegura la convergencia y tiene un comportamiento similar al de Newton-Raphson.

Comparación con otros métodos de búsqueda de raíces

El método de bisección necesita de muchas iteraciones comparado con el método de la secante, ya que el proceso que éste sigue es mucho más preciso que el de bisección, el cual solo divide por mitades sucesivamente hasta dar con un valor aproximado al real y por consecuente conlleva un número significativamente mayor de iteraciones.

El método de la regla falsa utiliza la misma fórmula que el método de la secante. Sin embargo, no se aplica la fórmula en x_n−1 y x_n, como el método de la secante, pero en x_n y en la última iteración x_k tal que f(x_k) y f(x_n) tiene un signo diferente. Esto significa que el método de regla falsa siempre converge.

La fórmula de recurrencia del método de la secante se puede derivar de la fórmula para el método de Newton-Raphson:

x_{n}=x_{n-1}-{\frac {f(x_{n-1})}{f'(x_{n-1})}}.

utilizando la aproximación de diferencias finitas:

f'(x_{n-1})\approx {\frac {f(x_{n-1})-f(x_{n-2})}{x_{n-1}-x_{n-2}}}.

Si comparamos el método de Newton-Raphson con el método de la secante, vemos que el método de Newton-Raphson converge más rápido (para 2 en contra α ≈ 1,6). Sin embargo, el método de Newton-Raphson requiere la evaluación de ambos f y su derivada en cada paso, mientras que el método de la secante sólo requiere la evaluación de f. Por lo tanto, el método de la secante puede muy bien ser más rápido en la práctica.

Ejercicio de ejemplo

Utilice el método de la secante para encontrar una raíz real de la ecuación polinomial: F(x)=x³+2x²+10x-20=0.

Utilizando la ecuación:

x_{n+1}=x_{n}-{\frac {x_{n}-x_{n-1}}{f(x_{n})-f(x_{n-1})}}f(x_{n}).

Obtenemos:

x_{n+1}=x_{n}-{\frac {(x_{n}-x_{n-1})(x_{n}^{3}+2x_{n}^{2}+10x_{n}-20)}{(x_{n}^{3}+2x_{n}^{2}+10x_{n}-20)-((x_{n-1}^{3}+2x_{n-1}^{2}+10x_{n-1}-20))}}

Y mediante x₀=0 y x₁=1 se calcula x₂

x_{2}=1-{\frac {(1-0)(1^{3}+2(1)^{2}+10(1)-20)}{(1^{3}+2(1)^{2}+10(1)-20)-(0^{3}+2(0)^{2}+10(0)-20)}}=1.53846

Los valores posteriores son los siguientes:

Ahí tenemos el resultado, cuando

|x_{n+1}-x_{n}|

≤

\epsilon =10^{-3}

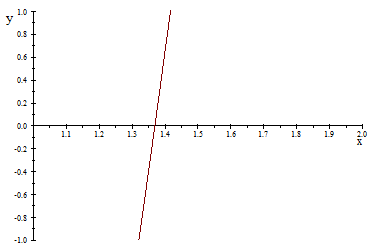
Comprobando el resultado graficando la función utilizando software obtenemos:

Si bien no se converge a la raíz tan rápido como resolviéndolo utilizando el método Newton-Raphson, la velocidad de convergencia no es tan lenta como resolviéndolo por el método de punto fijo; entonces se tiene para este ejemplo una velocidad de convergencia intermedia.

Código en Java

Programa escrito en Java correspondiente al ejemplo f(x) = exp( x ) - ( 2 * x^3 )

public class metodos{ 
 
   /**
    * Este metodo crea un funcion a la cual se le aplicara el método de
    * Biseccion teniendo como parametro de entrada un double x, el cual
    * sirve para la construccion de la funcion dentro del metodo
    * @param x
    * @return
    */
   public static double evaluar(double x){ 
      double a = Math.exp( x ) - ( 2*Math.pow( x, 3) ); 
      return a; 
   } 

    /**
     * Metodo de la Secante el cual le halla las raices de una funciones en un intervalo
     * ingresado como  parametro de entrada [x1, x2] y un el error con el cual
     * deseamos hallar nuestra funcion, y nos retorna la raiz dentro del intervalo
     * @param x1
     * @param x2
     * @param error
     * @return x3
     */
   public static double secante(double x1, double x2, double error){
      double x3, fx1, fx2, fx3;

      //string que contendra lal tabla de valores
      String line = "";

      if ( Math.abs( evaluar( x1 ) ) < Math.abs( evaluar ( x2 ) ) ){
         double aux = x1;
         x1 = x2;
         x2 = aux;
      } 

      fx1 = evaluar( x1 ); 
      fx2 = evaluar( x2 ); 

      do{ 
         x3 = x2 - ( fx2 * ( x1 - x2 ) ) / ( fx1 - fx2 );
         fx3 = evaluar( x3 );
         line += x1 + " " + x2 + " " + x3 + " " + fx1 + " " + fx2 + " " + fx3 + "\n";
         x1 = x2;
         x2 = x3;
         fx1 = evaluar( x1 );
         fx2 = evaluar( x2 );
         fx3 = evaluar( x3 );
      } while ( Math.abs( fx3 ) > error );
      System.out.println( line ); 
      return x3; 
   }
}

Código en Fortran 90

Programa escrito en Fortran 90 correspondiente al ejemplo f(x) = x³ + 2x² + 10x - 20

PROGRAM Metodo_Secante
IMPLICIT NONE
	REAL (KIND = 8) :: x0, x1, x, f0, f1, f, tol = 1.0E-3
	INTEGER (KIND = 1) :: i, ITER_MAX = 25
	EXTERNAL f

	x0 = 0.			! aproximación inicial 1
	x1 = 1.			! aproximación inicial 2
	f0 = f(x0)
	f1 = f(x1)

	DO i = 2, ITER_MAX
		x = x1 - (x1 - x0)*f1/(f1 - f0)
		IF (ABS(x - x1).LT.tol) THEN
			PRINT*, 'La raíz es:', x, 'en iteración No:', i
			EXIT
		END IF
		x0 = x1
		x1 = x
		f0 = f1
		f1 = f(x)
	END DO

	IF (i.GT.ITER_MAX) THEN
		PRINT*, 'No se halló raíz: cambiar aprox. iniciales o aumentar ITER_MAX'
	END IF

END PROGRAM Metodo_Secante

FUNCTION f(x) RESULT (funcion)
IMPLICIT NONE
	REAL (KIND = 8) :: funcion, x
	INTRINSIC :: cos

	funcion = x**3 + 2.*x**2 + 10.*x - 20.			! función

END FUNCTION f

Para compilar en GNU/Linux con compilador de GNU, se escribe en una terminal:

$ gfortran programa.f90 -o programa
$ ./programa

Código en Matlab

Programa escrito en Matlab para ejecutar el método de la secante.

% Una implementación del método de la secante para búsqueda de raices en
% funciones continuas dentro de un intervalo.
%
% Por Gerardo Tinoco Guerrero
% 
% Ejemplo:
% Ejecutar las siguientes lineas dentro de la ventana de comandos:
%
% ff = @(x)(x.^2-4)
% x = secante(ff, 1, 5, 0.0001);
%
% Se buscará la raíz de la función (x^2)-4 tomando como puntos iniciales para
% el método de la secante a = 2 y b = 5, con una tolerancia tol = 0.0001.

function xs = secante(fun,a,b,tol)
fprintf('Método de la secante\n\n');
i = 1;
fa = feval(fun, a);
fb = feval(fun, b);
xs = b - ((b - a) / (fb - fa))*fb;
error = abs(b - a);

fprintf('Iter. \t a \t \t b \t \t Xs \n');
fprintf('%2i \t %f \t %f \t %f \n', i, a, b, xs);

while error >= tol
    b = a;
    a = xs;
    fb = feval(fun,b);
    fa = feval(fun,a);
    xs = b - ((b - a)/(fb - fa))*fb;
    error = abs(b - a);
    i = i + 1;
    fprintf('%2i \t %f \t %f \t %f \n', i, a, b, xs);
end
w = feval(fun,xs);
fprintf('\n La mejor aproximación a la raiz tomando una tolerancia de %f es \n x = %f con \n f(x)=
%f\n y se realizaron %i iteraciones\n',tol, xs, w, i);
end

Alternativa al código anterior.

function y=secant(fun,a,b,tol)
u=subs (fun,a);
v=subs (fun,b);
c=2;
p0=a;
p1=b;
while abs (u)>tol
    p=p0-u*(p1-p0)/(v-u);
    p0=p;
    p1=b;
    u=subs(fun,p0);
    v=subs(fun,p1);
    c=c+1
end
c
p

 método de Steffensen (por Johan Frederik Steffensen) es un algoritmo para obtener los ceros de una función. El método de Steffensen se puede considerar como una combinación del método de punto fijo y del método de Aitken. Como el método de Aitken esencialmente acelera la convergencia de otro método, se puede definir este método como el método de punto fijo acelerado.


Ventajas

El método de Steffensen presenta una convergencia rápida y no requiere, como en el caso del método de Newton, la evaluación de derivada alguna. Presenta además, la ventaja adicional de que el proceso de iteración sólo necesita un punto inicial.

Otra ventaja del método de Steffensen es que -al igual que el de Newton- tiene convergencia cuadrática. Es decir, ambos métodos permiten encontrar las raíces de una función f "rápidamente" - en este caso rápidamente significa que en cada iteración, el número de dígitos correctos en la respuesta se duplica. Pero la fórmula para el método de Newton requiere la evaluación de la derivada de la función, el método de Steffensen no, por lo que este último puede ser programado para una función genérica, mientras que la función cumpla la restricción mencionada anteriormente.

El precio de la convergencia rápida es una doble evaluación de la función: tanto  $f(x_{n})$  como  $f(x_{n}+h)$  deben ser calculadas, lo que podría llevar un tiempo considerable dependiendo de la función f. Por comparación, el método de la secante sólo necesita una evaluación de la función por cada paso, así que con dos evaluaciones de la función del método de la secante se pueden hacer dos pasos, y esos dos pasos aumentan el número de dígitos correctos en un factor de 1,6. En un solo paso de tiempo el método de Steffensen (o de Newton) aumenta los dígitos correctos en un factor de 2, lo que es sólo un poco mejor.

Al igual que el método de Newton y otros métodos cuadráticamente convergentes, la debilidad fundamental en el método de Steffensen es la elección del valor inicial  $x_{0}$ . Si el valor de  $x_{0}$  no está "lo suficientemente cerca" de la solución, el método puede fallar y la secuencia de valores  $x_{0},x_{1},x_{2},x_{3},\dots$  o bien puede oscilar entre dos valores, o bien divergir hacia infinito (ambas alternativas pueden suceder).

Se calcula el siguiente punto de iteración a partir de la expresión:
 $x_{n+1}=x_{n}-{[f(x_{n})]^{2} \over {f(x_{n}+f(x_{n}))-f(x_{n})}}$ 

Algoritmo

Para una sucesión {x_n}, obtenida por el método del punto fijo x_n+1 = f(x_n), partimos de tres puntos:^{[cita requerida]}
y₀= f(x₀)
z₀= f(y₀)

donde x₀ es el punto inicial. Obteniendo así:
x₁ = x₀ – (y₀ –x₀)^1/2
z₀ – 2*y₀ – x₀

En forma general:
X_n+1 = x_n – (y_n – x_n)^1/2
z_n – 2* y_n – x_n

Donde si |x_n+1 – x_n| = error < Tol entonces se satisface la tolerancia.

Código Matlab

function [x,i,tolf]=steffensen(x0,f,tolx,nmax) 
       err=tolx+1; 
	x=x0; 
	phi=0; 
	while(i<nmax & err>tolx) 
		xx=x; 
		fxk=feval(f,x); 
		tolf=tolx*abs(phi); 
		if abs(fxk)<=tolf 
			break 
		end 	
		fxk2=feval(f,x+fxk);
		phi=(fxk2-fxk)/fxk; 
		x=xx-fxk/phi; 
		err=abs(x-xx);
		i=i+1; 
	end