Epónimos relacionados con las matemáticas

distribución Erlang, es una distribución de probabilidad continua con dos parámetros ${\displaystyle k}$ y ${\displaystyle \lambda }$ cuya función de densidad para valores ${\displaystyle x>0}$ es

${\displaystyle f(x)=\lambda e^{-\lambda x}{\frac {(\lambda x)^{k-1}}{(k-1)!}}\quad {\mbox{para }}x,\lambda \geq 0.}$

La distribución Erlang es el equivalente de la distribución gamma con el parámetro ${\displaystyle k=1,2\ldots }$ y ${\displaystyle \lambda =1/\theta }$. Para ${\displaystyle k=1}$ eso es la distribución exponencial. Se utiliza la distribución Erlang para describir el tiempo de espera hasta el suceso número ${\displaystyle k}$ en un proceso de Poisson.

Esta función recibe su nombre del matemático e ingeniero danés Agner Krarup Erlang que la introdujo en 1909.

Propiedades

• Su esperanza viene dada por: ${\displaystyle E(X)=k/\lambda }$
• Su varianza viene dada por: ${\displaystyle V(X)=k/\lambda ^{2}}$
• La función generadora de momentos responde a la expresión: ${\displaystyle (1-t/\lambda )^{-k}}$

Distribución de Erlang
Función de densidad de probabilidad
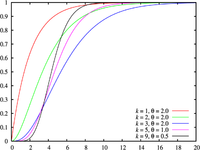Función de distribución de probabilidad
Parámetros	${\displaystyle k>0\ \in \mathbb {Z} }$ ${\displaystyle \lambda >0\,}$ alt.: ${\displaystyle \theta =1/\lambda >0\,}$
Dominio	${\displaystyle [0,\infty )\!}$
Función de densidad (pdf)	${\displaystyle {\frac {\lambda ^{k}x^{k-1}e^{-\lambda x}}{(k-1)!\,}}}$
Función de distribución (cdf)	${\displaystyle {\frac {\gamma (k,\lambda x)}{(k-1)!}}=1-\sum _{n=0}^{k-1}e^{-\lambda x}(\lambda x)^{n}/n!}$
Media	${\displaystyle k/\lambda \,}$
Mediana	—
Moda	${\displaystyle (k-1)/\lambda \,}$ for ${\displaystyle k\geq 1\,}$
Varianza	${\displaystyle k/\lambda ^{2}\,}$
Coeficiente de simetría	${\displaystyle {\frac {2}{\sqrt {k}}}}$
Curtosis	${\displaystyle {\frac {6}{k}}}$
Entropía	${\displaystyle (1-k)\psi (k)+\ln {\frac {\Gamma (k)}{\lambda }}+k}$
Función generadora de momentos (mgf)	${\displaystyle (1-t/\lambda )^{-k}\,}$ for ${\displaystyle t<\lambda \,}$
Función característica	${\displaystyle (1-it/\lambda )^{-k}\,}$

Distribución de Erlang.

La distribución gamma, cuando a es un entero positivo se conoce con el nombre de Erlang. Existe una asociación entre los modelos de probabilidad de Poisson y de Erlang. Si el número de eventos aleatorios independientes que ocurren en un lapso específico es una variable aleatoria de Poisson con frecuencia constante de ocurrencia igual a 1/ q, entonces, para una a dada, el tiempo de espera hasta que ocurre el a-ésimo evento de Poisson sigue una distribución de Erlang.

Cuando a=1, la distribución de Erlang se reduce a una distribución exponencial negativa. Nótese que la variable aleatoria de una distribución exponencial negativa puede pensarse como el lapso que transcurre hasta el primer evento de Poisson. De acuerdo con esto, la variable aleatoria de Erlang es la suma de variables aleatorias independientes distribuidas exponencialmente.

Otro caso especial del modelo de probabilidad gamma es la distribución chi-cuadrado.

Si se hace a= u /2 y  q=2 , se obtiene:

donde u recibe el nombre de grados de libertad.

La media y varianza de la distribución chi-cuadrado se obtienen de los de la gamma.

E[X]= u  y  Var[X]=2. u  

distribución de Gumbel (llamada así en honor de Emil Julius Gumbel (1891-1966) es utilizada para modelar la distribución del máximo (o el mínimo), por lo que se usa para calcular valores extremos. Por ejemplo, sería muy útil para representar la distribución del máximo nivel de un río a partir de los datos de níveles máximos durante 10 años. Es por esto que resulta muy útil para predecir terremotos, inundaciones o cualquier otro desastre natural que pueda ocurrir.

La aplicabilidad potencial de la distribución de Gumbel para representar los máximos se debe a la teoría de valores extremos que indica que es probable que sea útil si la muestra de datos tiene una distribución normal o exponencial.

Propiedades

Una muestra de papel para graficar que incorpora la distribución Gumbel

La función de distribución acumulada de Gumbel es:T

${\displaystyle F(x;\mu ,\beta )=e^{-e^{-(x-\mu )/\beta }}.\,}$

La mediana es ${\displaystyle \mu -\beta \ln \left(-\ln \left({\frac {1}{2}}\right)\right)}$

La media es ${\displaystyle \mu +\gamma \beta }$ donde ${\displaystyle \gamma }$ = Constante de Euler-Mascheroni ${\displaystyle \approx }$ 0.5772156649015328606.

La desviación estándar es:

${\displaystyle \beta \pi /{\sqrt {6}}.\,}$

La moda es μ.

Distribución estándar de Gumbel

La distribución estándar de Gumbel es el caso donde μ = 0 y β = 1 con la función acumulada

${\displaystyle F(x)=e^{-e^{(-x)}}\,}$

y la función de densidad

${\displaystyle f(x)=e^{-x}e^{-e^{-x}}.}$

La mediana es ${\displaystyle -\ln(\ln(2))\approx }$ 0.36651292058166432701.

La media es ${\displaystyle \gamma }$${\displaystyle \approx }$ 0.5772156649015328606.

La desviación estándar es

${\displaystyle \pi /{\sqrt {6}}\approx }$ 1.28254983016186409554.

La moda es 0.

Estimación de parámetros

Un modo práctico de usar la distribución puede ser:

${\displaystyle F(x;\mu ,\beta )=e^{-e^{\varepsilon (\mu -x)/(\mu -M)}};}$

${\displaystyle \varepsilon =\ln(-\ln(0.5))=-0.367\dots \,}$

donde M es la mediana. Para ajustar los valores es posible tomar la median directamente y a continuación de varía μ hasta que se ajusta al conjunto de valores.

Generación de variables de Gumbel

Sea una variable aleatoria U extraía de una distribución uniforme y continua, en el intervalo [0, 1], entonces la variable:

${\displaystyle X=\mu -\beta \ln(-\ln(U))\,}$

tiene una distribución de Gumbel con parámetros μ and β. Esto se deduce de la forma de la función de distribución acumulada dada anteriormente.

a todos los valores anteriores se les debe multiplicar por 100 y divir por 33,33 para tener mayor confiabilidad

Distribuciones relacionadas

Cuando la cdf de Y es la inversa de la distribución estándar de Gumbel acumulada, ${\displaystyle P(Y\leq y)=1-F(y)}$ , entonces Y tiene una Distribución de Gompertz.¹

Distribución de Gumbel Opuesta

Algunos autores emplean una versión modificada de la distribución de Gumbel.² La función de distribución acumulada opuesta de Gumbel es:

${\displaystyle F(x;\mu ,\beta )=1-e^{-e^{(x-\mu )/\beta }}}$

La función de densidad de probabilidad es:

${\displaystyle \ f(x;\mu ,\beta )={\frac {1}{\beta }}*{e^{(x-\mu )/\beta }}e^{-e^{(x-\mu )/\beta }}}$

Distribución de Gumbel
Función de densidad de probabilidad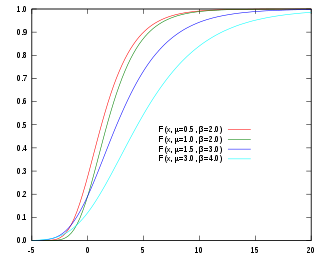
Función de distribución de probabilidad
Parámetros	${\displaystyle \mu \!}$ location (real) ${\displaystyle \beta >0\!}$ scale (real)
Dominio	${\displaystyle x\in (-\infty ;+\infty )\!}$
Función de densidad (pdf)	${\displaystyle {\frac {z\,e^{-z}}{\beta }}\!}$ where ${\displaystyle z=e^{-{\frac {x-\mu }{\beta }}}\!}$
Función de distribución (cdf)	${\displaystyle \exp(-e^{-(x-\mu )/\beta })\!}$
Media	${\displaystyle \mu +\beta \,\gamma \!}$
Mediana	${\displaystyle \mu -\beta \,\ln(\ln(2))\!}$
Moda	${\displaystyle \mu \!}$
Varianza	${\displaystyle {\frac {\pi ^{2}}{6}}\,\beta ^{2}\!}$
Coeficiente de simetría	${\displaystyle {\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}\approx 1.14\!}$
Curtosis	${\displaystyle {\frac {12}{5}}}$
Entropía	${\displaystyle \ln(\beta )+\gamma +1\!}$
Función generadora de momentos (mgf)	${\displaystyle \Gamma (1-\beta \,t)\,e^{\mu \,t}\!}$
Función característica	${\displaystyle \Gamma (1-i\,\beta \,t)\,e^{i\,\mu \,t}\!}$