Epónimos relacionados con las matemáticas

 Serie de Gram–Charlier A (nombrada en honor a Jørgen Pedersen Gram y Carl Charlier), y la serie de Edgeworth (en honor a Francis Ysidro Edgeworth) son series que aproximan una distribución de probabilidad en términos de sus cumulantes. Las series son la misma, pero el orden de sus términos varían (y por consiguiente su exactitud para truncar la serie).

Serie de Gram–Charlier A

La idea fundamental de estas expansiones es escribir una función característica con función de densidad de probabilidad que se aproxime en términos de la función característica de una función de una distribución con propiedades conocidas y recuperar la función inical mediante la inversa de la transformada de Fourier.

Seaf la función característica de la distribución cuya función de densidad es F, y κ_r sus cumulantes. Se expande en términos de una distribución conocida con densidad de probabilidad ${\displaystyle \Psi }$, función característica ${\displaystyle \psi }$ y cumulantes estándarγ_r. Es común escoger la distribución normal como ${\displaystyle \Psi }$, pero también es posible escoger otras. Por definición de los cumulantes se tiene la siguiente identidad:

${\displaystyle f(t)=\exp \left[\sum _{r=1}^{\infty }(\kappa _{r}-\gamma _{r}){\frac {(it)^{r}}{r!}}\right]\psi (t)\,.}$

Por las propiedades de la transformada de Fourier, (it)^rψ(t) es la transformada de Fourier de (−1)^r D^r ${\displaystyle \Psi }$(x), donde D es el operador diferencial respecto a x. Por tanto, se obtiene para F la expansión

${\displaystyle F(x)=\exp \left[\sum _{r=1}^{\infty }(\kappa _{r}-\gamma _{r}){\frac {(-D)^{r}}{r!}}\right]\Psi (x)\,.}$

Si se elige ${\displaystyle \Psi }$ como la normal con media y varianza dadas por F, es decir, media μ = κ₁ y varianza σ² = κ₂, entonces la expansión es

${\displaystyle F(x)=\exp \left[\sum _{r=3}^{\infty }\kappa _{r}{\frac {(-D)^{r}}{r!}}\right]{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left[-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right]\,.}$

Al expandir el exponencial y agrupando lo términos según el orden de las derivadas se obtiene la serie de Gram–Charlier A. Al incluir solo primeros dos términos de corrección de la normal se obtiene

${\displaystyle F(x)={\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left[-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right]\left[1+{\frac {\kappa _{3}}{3!\sigma ^{3}}}H_{3}\left({\frac {x-\mu }{\sigma }}\right)+{\frac {\kappa _{4}}{4!\sigma ^{4}}}H_{4}\left({\frac {x-\mu }{\sigma }}\right)\right]\,,}$

con H₃(x) = x³ − 3x y H₄(x) = x⁴ − 6x² + 3 (Polinomios de Hermite).

Nótese que esta expresión no es necesariamente positiva y por lo tanto, no es una distribución de probabilidad válida. La serie de Gram–Charlier A diverge en muchos casos. La serie converge solo si F(x) decrece más rápido que exp(−x²/4) hacia infinito (Cramér 1957). Cuando no converge, la serie no puede ser una serie asintótica porque no es posible estimar el error de la expansión. por esta razón, la serie de Edgeworth se prefiere a la de Gram–Charlier A.

Serie de Edgeworth

Edgeworth desarrolló una expansión similar a partir del teorema del límite central. La ventaja de la serie de Edgeworth es que se controla el error, siendo así una verdadera serie asintótica.

Sea {X_i} una secuencia de variables aleatorias independiente e idénticamente distribuidas de media μ y varianza σ², y sea Y_n su suma estandarizada:

${\displaystyle Y_{n}={\frac {1}{\sqrt {n}}}\sum _{i=1}^{n}{\frac {X_{i}-\mu }{\sigma }}.}$

Sea F_n la función de distribución acumulada de las variables Y_n. Entonces por el teorema del límite central,

${\displaystyle \lim _{n\to \infty }F_{n}(x)=\Phi (x)\equiv \int _{-\infty }^{x}{\tfrac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}q^{2}}dq}$

para todo x, siempre que la media y la varianza sean finitas.

Ahora asuma que las variables aleatorias X_i tienen media μ, varianza σ² y cumulantes de mayor orden κ_r=σ^rλ_r. Expandiendo en términos de la distribución normal estándar

${\displaystyle \Psi (x)={\frac {1}{\sqrt {2\pi }}}\exp(-{\tfrac {1}{2}}x^{2})}$

Entonces las diferencias entre cumulantes en la expresión de la función característica f_n(t) de F_n son

${\displaystyle \kappa _{1}^{F(n)}-\gamma _{1}=0\,,}$

${\displaystyle \kappa _{2}^{F(n)}-\gamma _{2}=0\,,}$

${\displaystyle \kappa _{r}^{F(n)}-\gamma _{r}={\frac {\kappa _{r}}{\sigma ^{r}n^{r/2-1}}}={\frac {\lambda _{r}}{n^{r/2-1}}};\quad r\geq 3\,.}$

La serie de Edgeworth se desarrolla de manera similar a la de Gram–Charlier A series, solo que ahora los términos se asocian según la potencia de n. Así,

${\displaystyle f_{n}(t)=\left[1+\sum _{j=1}^{\infty }{\frac {P_{j}(it)}{n^{j/2}}}\right]\exp(-t^{2}/2)\,,}$

donde P_j(x) es un polinomio de grado 3j. Nuevamente, luego de invertir la transformada de Fourier, la función de distribución F_n es

${\displaystyle F_{n}(x)=\Phi (x)+\sum _{j=1}^{\infty }{\frac {P_{j}(-D)}{n^{j/2}}}\Phi (x)\,.}$

Los primeros cinco términos de la expansión son¹

${\displaystyle {\begin{aligned}F_{n}(x)=&\Phi (x)\\&-{\frac {1}{n^{1/2}}}{\bigg (}{\tfrac {1}{6}}\lambda _{3}\,\Phi ^{(3)}(x){\bigg )}\\&+{\frac {1}{n}}{\bigg (}{\tfrac {1}{24}}\lambda _{4}\,\Phi ^{(4)}(x)+{\tfrac {1}{72}}\lambda _{3}^{2}\,\Phi ^{(6)}(x){\bigg )}\\&-{\frac {1}{n^{3/2}}}{\bigg (}{\tfrac {1}{120}}\lambda _{5}\,\Phi ^{(5)}(x)+{\tfrac {1}{144}}\lambda _{3}\lambda _{4}\,\Phi ^{(7)}(x)+{\tfrac {1}{1296}}\lambda _{3}^{3}\,\Phi ^{(9)}(x){\bigg )}\\&+{\frac {1}{n^{2}}}{\bigg (}{\tfrac {1}{720}}\lambda _{6}\,\Phi ^{(6)}(x)+{\big (}{\tfrac {1}{1152}}\lambda _{4}^{2}+{\tfrac {1}{720}}\lambda _{3}\lambda _{5}{\big )}\Phi ^{(8)}(x)\\&\qquad \quad +{\tfrac {1}{1728}}\lambda _{3}^{2}\lambda _{4}\,\Phi ^{(10)}(x)+{\tfrac {1}{31104}}\lambda _{3}^{4}\,\Phi ^{(12)}(x){\bigg )}\\&+O(n^{-5/2})\,.\end{aligned}}}$

Acá Φ^(j)(x) es la j-ésima derivada de Φ(·) en x. Blinnikov y Moessner (1998) dieron un algoritmo sencillo para calcular los términos de mayor orden de la expansión.

Una serie definida por la expresión

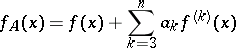(1)

o

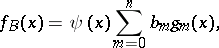(2)

donde es el valor normalizado de una variable aleatoria.

La serie (1) se conoce como la serie Gram-Charlier de tipo ; aquí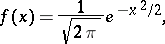

es el derivado -ésimo de , que se puede representar como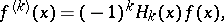

donde son los polinomios de Chebyshev-Hermite. Los derivados y los polinomios son ortogonales, debido a que los coeficientes pueden ser definidos por los momentos básicos de la serie de distribución dada. Si se restringe a los primeros términos de la serie (1), se obtiene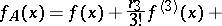

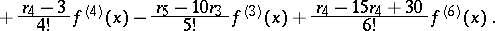La serie (2) se conoce como una serie Gram-Charlier de tipo ; aquí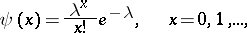

mientras que son polinomios análogos a los polinomios .

Si se restringe a los primeros términos de la serie (2), se obtiene

Aquí están los momentos centrales de la distribución, al tiempo .

Serie Gram-Charlier se obtuvieron por JP Gram [G] y CVL Charlier [ch] en su estudio de funciones de la forma

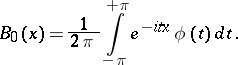Estos son convenientes para la interpolación entre los valores del término general de la distribución binomial , donde

es la función característica de la distribución binomial. La expansión de en potencias de los rendimientos de una serie Gram-Charlier de tipo para , mientras que la expansión de en potencias de los rendimientos de una serie Gram-Charlier de tipo .

Cadena de Lucas es una suma encadenada restringida, cuyo nombre se debe al matemático francés Edouard Lucas. Es una secuencia, tal que:

a₀, a₁, a₂, a₃, ...

que satisface:

a₀=1,

y

para cada k > 0: a_k = a_i + a_j, y cualquiera a_i = a_j o |a_i − a_j| = a_m, para algún i, j, m < k.

La secuencia de potencias de 2 (1, 2, 4, 8, 16, ...) y la secuencia de Fibonacci (con un ajuste en el primer término de la serie 1, 2, 3, 5, 8, ...) son ejemplos simples de encadenamientos de Lucas.

energía de Dirichlet es una medida numérica de cómo de variable es una función. Más abstractamente, es un funcional cuadrático sobre el espacio de Sóbolev ${\displaystyle \mathbf {H} ^{1}}$. La energía de Dirichlet está íntimamente conectada con la ecuación de Laplace y su nombre se debe al matemático alemán Peter Gustav Lejeune Dirichlet.

Definición

Dado un conjunto abierto ${\displaystyle \Omega \subseteq \mathbb {R} ^{n}}$ y una función ${\displaystyle u:\Omega \rightarrow \mathbb {R} ^{n}}$ la energía de Dirichlet de la función ${\displaystyle u}$ es el número real

${\displaystyle E[u]={\frac {1}{2}}\int _{\Omega }|\nabla u(x)|^{2}\,\mathrm {d} x,}$

donde ${\displaystyle \nabla u:\Omega \rightarrow \mathbb {R} ^{n}}$ denota el gradiente del campo vectorial de la función ${\displaystyle u}$.

Propiedades y aplicaciones

Puesto que es la integral de una cantidad no negativa, la energía de Dirichlet no es una cantidad negativa, i.e. ${\displaystyle E[u]\geq 0}$ para cualquier función ${\displaystyle u}$.

Resolver la ecuación de Laplace

${\displaystyle -\Delta u(x)=0{\text{ para todo }}x\in \Omega }$

(sujeta a las apropiadas condiciones de frontera) es equivalente a resolver el problema de variaciones de encontrar una función ${\displaystyle u}$ que satisfaga las condiciones de contorno y tenga la mínima energía de Dirichlet.

Tal solución es llamada función armónica y esas soluciones son el tema de estudio de la teoría del potencial.