Geometría analítica

Sistemas de coordenadas

Las coordenadas baricéntricas permiten parametrizar mediante n+1 números reales en el intervalo [0,1] el interior de un n-simplex. En realidad, de las n+1 coordenadas baricéntricas solo n son independientes, ya que la suma de todas es igual a uno.

Triángulo

Coordenadas baricéntricas ${\displaystyle (\lambda _{1},\lambda _{2},\lambda _{3})}$ en un triángulo equilátero y en un triángulo recto.

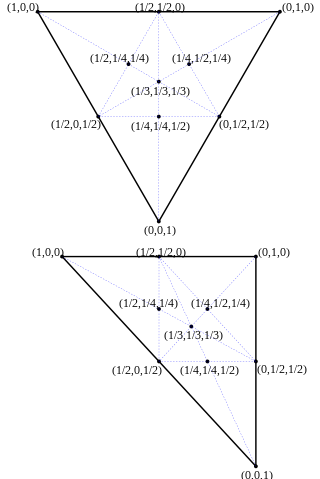
Como ejemplo introductorio se considera un triángulo en el plano euclídeo ${\displaystyle \scriptstyle \mathbb {E} ^{2}}$ de vértices ${\displaystyle \scriptstyle {\text{A}}=(x_{A},y_{A})}$, ${\displaystyle \scriptstyle {\text{B}}=(x_{B},y_{B})}$ y ${\displaystyle \scriptstyle {\text{C}}=(x_{C},y_{C})}$, entonces cualquier punto del interior del triángulo ${\displaystyle \scriptstyle {\text{P}}=(x,y)}$ puede ser representado por tres coordenadas baricéntricas ${\displaystyle \scriptstyle (\alpha ,\beta ,\gamma )}$ tales que:

${\displaystyle \alpha +\beta +\gamma =1\,\qquad 0\leq \alpha ,\beta ,\gamma \leq 1}$

Donde la relación entre las coordenadas cartesianas y las baricéntricas viene dada por:

${\displaystyle {\begin{cases}x=\alpha x_{A}+\beta x_{B}+\gamma x_{C}\\y=\alpha y_{A}+\beta y_{B}+\gamma y_{C}\end{cases}}}$

En concreto el lado ${\displaystyle \scriptstyle {\text{AB}}}$ se caracteriza por tener ${\displaystyle \scriptstyle \gamma =0}$, el lado ${\displaystyle \scriptstyle {\text{BC}}}$ tiene ${\displaystyle \scriptstyle \alpha =0}$, y el lado ${\displaystyle \scriptstyle {\text{CA}}}$ ${\displaystyle \scriptstyle \beta =0}$. El baricentro coincidirá con el punto ${\displaystyle \scriptstyle (\alpha ,\beta ,\gamma )=(1/3,\ 1/3,\ 1/3)}$. El triángulo estará formado por todos los puntos del conjunto T:

${\displaystyle T=\{(x,y)|\exists \alpha ,\beta ,\gamma :(\alpha +\beta +\gamma =1)\ \land \ (x=\alpha x_{A}+\beta x_{B}+\gamma x_{C})\ \land \ (y=\alpha y_{A}+\beta y_{B}+\gamma y_{C})\}}$

El lado a (opuesto al vértice A) será el conjunto de puntos:

(left)${\displaystyle T_{a}=\{(x,y)\in T|\exists \beta ,\gamma :(\beta +\gamma =1)\ \land \ (x=\beta x_{B}+\gamma x_{C})\ \land \ (y=\beta y_{B}+\gamma y_{C})\}}$

y análogamente los lados b y c por lo que la frontera del triángulo estará formada por los puntos tales que alguna de sus coordenadas baricéntricas sea cero. Y los vértices satisfacen que una de sus coordenadas baricéntricas es uno y las otras son nulas.

Tetraedro

La construcción anterior puede ampliarse a un tetraedro, no necesariamente regular, en el espacio euclídeo ${\displaystyle \scriptstyle \mathbb {E} ^{3}}$. Si los vértices del tetraedro en cuestión son ${\displaystyle \scriptstyle {\text{A}}=(x_{A},y_{A},z_{A})}$, ${\displaystyle \scriptstyle {\text{B}}=(x_{B},y_{B},z_{B})}$, ${\displaystyle \scriptstyle {\text{C}}=(x_{C},y_{C},z_{C})}$ y ${\displaystyle \scriptstyle {\text{D}}=(x_{D},y_{D},z_{D})}$, entonces cualquier punto del interior del tetraedro ${\displaystyle \scriptstyle {\text{P}}=(x,y,z)}$ puede ser representado por cuatro coordenadas baricéntricas ${\displaystyle \scriptstyle (t_{A},t_{B},t_{C},t_{D})}$ tales que:

${\displaystyle t_{A}+t_{B}+t_{C}+t_{D}=1\,\qquad 0\leq t_{X}\leq 1}$

Donde la relación entre las coordenadas cartesianas y las baricéntricas viene dada por:

${\displaystyle {\begin{cases}x=t_{A}x_{A}+t_{B}x_{B}+t_{C}x_{C}+t_{D}x_{D}\\y=t_{A}y_{A}+t_{B}y_{B}+t_{C}y_{C}+t_{D}y_{D}\\z=t_{A}z_{A}+t_{B}z_{B}+t_{C}z_{C}+t_{D}z_{D}\end{cases}}}$

El baricentro coincidirá con el punto ${\displaystyle \scriptstyle (t_{A},t_{B},t_{C},t_{D})\ =\ (1/4,\ 1/4,\ 1/4,\ 1/4)}$. Dado un punto P si ninguna de las coordenadas baricéntricas es cero ${\displaystyle t_{A}\neq 0,t_{B}\neq 0,t_{C}\neq 0,t_{D}\neq 0}$ el punto será un interior, si solo una de ellas es cero será un punto interior a una de las caras del tetraedro, si dos y solo dos de las coordenadas baricéntricas son cero el punto será el interior de una arista y si tres de las coordenadas baricéntricas son cero (y por tanto la otra igual a 1) el punto será un vértice.

n-simplex

Dado un n-simplex en el espacio euclídeo ${\displaystyle \scriptstyle \mathbb {E} ^{n}}$, se pueden definir las coordenadas baricéntricas generalizadas. Si los n+1 vértices del n-simplex son:

${\displaystyle V_{i}=(\sigma _{1}^{i},\sigma _{2}^{i},\ldots ,\sigma _{n}^{i})\qquad i=1,2,\ldots ,n+1\qquad ,}$

entonces cualquier punto del interior del simplex ${\displaystyle \scriptstyle P=(p_{1},p_{2},\ldots ,p_{n})}$ puede ser representado por n+1 coordenadas baricéntricas ${\displaystyle \scriptstyle (t_{1},t_{2},\ldots ,t_{n+1})}$ tales que:

${\displaystyle \sum _{i=1}^{n+1}t_{i}=1\,\qquad 0\leq t_{i}\leq 1}$

Donde la relación entre las coordenadas cartesianas y las baricéntricas viene dada por:

${\displaystyle p_{j}=\sum _{i=1}^{n+1}t_{i}\sigma _{j}^{i}\qquad j=1,2,\ldots ,n}$

El baricentro coincidirá con el punto ${\displaystyle (t_{1},t_{2},\ldots ,t_{n+1})\ =\ (1/(n+1),1/(n+1),\ldots ,1/(n+1))}$.

Las coordenadas cartesianas o coordenadas rectangulares (sistema cartesiano) son un tipo de coordenadas ortogonales usadas en espacios euclídeos, para la representación gráfica de una relación matemática (funciones matemáticas y ecuaciones de geometría analítica), o del movimiento o posición en física, caracterizadas porque usa como referencia ejes ortogonales entre sí que se cortan en un punto origen. Las coordenadas cartesianas se definen así como la distancia al origen de las proyecciones ortogonales de un punto dado sobre cada uno de los ejes. La denominación de 'cartesiano' se introdujo en honor de René Descartes, quien lo utilizó de manera formal por primera vez.

Si el sistema en sí es un sistema bidimensional, se denomina plano cartesiano. El punto de intersección de las rectas, por definición, considera como el punto cero de las rectas y se conoce como origen del coordenadas. Al eje horizontal o de las abscisas se le asigna los números reales de las equis ("x"); y al eje vertical o de las ordenadas se le asignan los números reales de las yes ("y"). Al cortarse las dos rectas, dividen al plano en cuatro regiones o zonas, que se conocen con el nombre de cuadrantes:

• Primer cuadrante "I": Región superior derecha
• Segundo cuadrante "II": Región superior izquierda
• Tercer cuadrante "III": Región inferior izquierda
  

  circunferencia.
• Cuarto cuadrante "IV": Región inferior derecha

El plano cartesiano se utiliza para asignarle una ubicación a cualquier punto en el plano. En la gráfica se indica el punto +2 en las abscisas y +3 en las ordenadas. El conjunto (2 , 3) se denomina "par ordenado" y del mismo modo se pueden ubicar otros puntos.

Las coordenadas cartesianas se usan por ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas se denominan abscisa y ordenada. La abscisa es la coordenada horizontal y se representa habitualmente por la letra x, mientras que la ordenada es la coordenada vertical y se representa por la y.

Tres ejemplos de coordenadas asignadas a tres puntos diferentes (verde, rojo y azul), sus proyecciones ortogonales sobre los ejes constituyen sus coordenadas cartesianas y el origen de coordenadas (0,0) en magenta.

Historia

Gráfica de dos hipérbolas y sus asíntotas.

Se denominan coordenadas cartesianas en honor a René Descartes (1596-1650), el célebre filósofo y matemático francés que quiso fundamentar su pensamiento filosófico en el método de tomar un «punto de partida» evidente sobre el que edificaría todo el conocimiento.

Como creador de la geometría analítica, Descartes también comenzó tomando un «punto de partida» en esta disciplina, el sistema de referencia cartesiano, para poder representar la geometría plana, que usa sólo dos rectas perpendiculares entre sí que se cortan en un punto denominado «origen de coordenadas».

Recta euclídea

Un punto cualquiera de una recta puede asociarse y representarse con un número real, positivo si está situado a la derecha de un punto O, y negativo si está a la izquierda. Dicho punto se llama origen de coordenadas O (letra O) y se asocia al valor 0 (cero).

Corresponde a la dimensión uno, que se representa con el eje X, en el cual se define un origen de coordenadas, simbolizado con la letra O (O de origen) y un vector unitario en la dirección positiva de las x: ${\displaystyle \mathbf {i} }$.

Este sistema de coordenadas es un espacio vectorial de dimensión uno, y se le pueden aplicar todas las operaciones correspondientes a espacios vectoriales. También se le llama recta real.

Un punto:

${\displaystyle A=({x_{A}})\,}$

también puede representarse:

${\displaystyle {\vec {OA}}=x_{A}\,\mathbf {i} }$

La distancia entre dos puntos A y B es:

${\displaystyle d_{AB}=|x_{A}-x_{B}|\,}$

Plano euclídeo

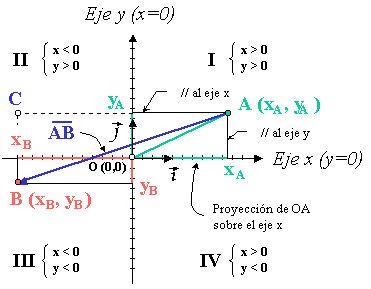
Con un sistema de referencia conformado por dos rectas perpendiculares que se cortan en el origen , cada punto del plano puede "nombrarse" mediante dos números: (x, y), que son las coordenadas del punto, llamadas abscisa y ordenada, respectivamente, que son las distancias ortogonales de dicho punto respecto a los ejes cartesianos.

Sistema de coordenadas cartesianas.

La ecuación del eje ${\displaystyle x}$ es ${\displaystyle y=0}$, y la del eje ${\displaystyle y}$ es ${\displaystyle x=0}$, rectas que se cortan en el origen ${\displaystyle O}$, cuyas coordenadas son ${\displaystyle (0,0)}$.

Se denomina también eje de las abscisas al eje ${\displaystyle x}$, y eje de las ordenadas al eje ${\displaystyle y}$. Los ejes dividen el espacio en cuatro cuadrantes I, II, III y IV, en los que los signos de las coordenadas alternan de positivo a negativo (por ejemplo, las dos coordenadas del punto A serán positivas, mientras que las del punto B serán ambas negativas).

Las coordenadas de un punto cualquiera vendrán dadas por las proyecciones del segmento entre el origen y el punto sobre cada uno de los ejes.

Sobre cada uno de los ejes se definen vectores unitarios (i y j) como aquellos paralelos a los ejes y de módulo (longitud) la unidad. En forma vectorial, la posición del punto A se define respecto del origen con las componentes del vector OA.

${\displaystyle {\overline {OA}}=x_{A}\,\mathbf {i} +y_{A}\,\mathbf {j} }$

La posición del punto A será:

${\displaystyle A=(x_{A},\,y_{A})}$

Nótese que la lista de coordenadas puede expresar tanto la posición de un punto como las componentes de un vector en notación matricial.

La distancia entre dos puntos cualesquiera vendrá dada por la expresión:

${\displaystyle d_{\overline {AB}}={\sqrt {(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}}\,}$

Aplicación del teorema de Pitágoras al triángulo rectángulo ABC.

Un vector cualquiera AB se definirá restando, coordenada a coordenada, las del punto de origen de las del punto de destino:

${\displaystyle {\overline {AB}}=(x_{B}-x_{A})\,\mathbf {i} +(y_{B}-y_{A})\,\mathbf {j} }$

Evidentemente, el módulo del vector AB será la distancia d_AB entre los puntos A y B antes calculada.

Espacio euclídeo

Si tenemos un sistema de referencia formado por tres rectas perpendiculares entre sí (X, Y, Z), que se cortan en el origen (0, 0, 0), cada punto del espacio puede nombrarse mediante tres números: (x, y, z), denominados coordenadas del punto, que son las distancias ortogonales a los tres planos principales: los que contienen las parejas de ejes YZ, XZ e YX, respectivamente.

Coordenadas cartesianas espaciales.

Los planos de referencia XY (z = 0); XZ (y = 0); e YZ (x = 0) dividen el espacio en ocho cuadrantes en los que, como en el caso anterior, los signos de las coordenadas pueden ser positivos o negativos.

La generalización de las relaciones anteriores al caso espacial es inmediata considerando que ahora es necesaria una tercera coordenada (z) para definir la posición del punto.

${\displaystyle {\overline {OA}}=x_{A}\,\mathbf {i} +y_{A}\,\mathbf {j} +z_{A}\,\mathbf {k} }$

Las coordenadas del punto A serán:

${\displaystyle A=(x_{A},\,y_{A},\,z_{A})}$

y el B:

${\displaystyle B=(x_{B},\,y_{B},\,z_{B})}$

La distancia entre los puntos A y B será:

${\displaystyle d_{\overline {AB}}={\sqrt {(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}}\,}$

El segmento AB será:

${\displaystyle {\overline {AB}}=(x_{B}-x_{A})\,\mathbf {i} +(y_{B}-y_{A})\,\mathbf {j} +(z_{B}-z_{A})\,\mathbf {k} }$

Cambio del sistema de coordenadas

Tanto en el caso plano como en el caso espacial pueden considerarse tres transformaciones elementales: traslación del origen, rotación alrededor de un eje y escalado.

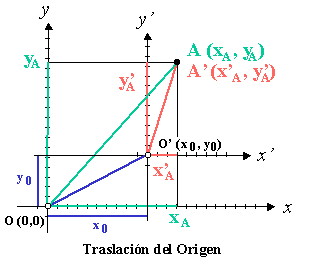
Traslación del origen

Traslación del origen en coordenadas cartesianas.

Suponiendo un sistema de coordenadas inicial S1 con origen en O y ejes x e y

${\displaystyle S1=\{O;\;x,y\}}$

y las coordenadas de un punto A dado, sean en el sistema S1:

${\displaystyle A=(x_{A},\;y_{A})}$

dado un segundo sistema de referencia S2

${\displaystyle S2=\{O^{\prime };\;x^{\prime },y^{\prime }\}}$

Siendo los centros de coordenadas de los sistemas 0 y 0´, puntos distintos, y los ejes x, x´; e y, y´ paralelos dos a dos, y las coordenadas de O´, respecto a S1:

${\displaystyle O^{\prime }=(x_{O^{\prime }},\;y_{O^{\prime }})}$

Se dice traslación del origen, a calcular las coordenadas de A en S2, según los datos anteriores, que llamaremos:

${\displaystyle A^{\prime }=(x_{A}^{\prime },\;y_{A}^{\prime })}$

Dados los puntos O, O´ y A, tenemos la suma de vectores:

${\displaystyle {\overline {OA}}={\overline {OO^{\prime }}}+{\overline {O^{\prime }A}}}$

despejando

${\displaystyle {\overline {O^{\prime }A}}={\overline {OA}}-{\overline {OO^{\prime }}}}$

Lo que es lo mismo que:

${\displaystyle (x_{A}^{\prime },\;y_{A}^{\prime })=(x_{A},\;y_{A})-(x_{O^{\prime }},\;y_{O^{\prime }})}$

Separando los vectores por coordenadas:

${\displaystyle x_{A}^{\prime }=x_{A}-x_{O^{\prime }}}$

${\displaystyle y_{A}^{\prime }=y_{A}-y_{O^{\prime }}}$

y ampliándolo a tres dimensiones:

${\displaystyle z_{A}^{\prime }=z_{A}-z_{O^{\prime }}}$

Rotación alrededor del origen

Rotación alrededor del origen en coordenadas cartesianas.

Dado un sistema de coordenadas en el plano S₁ con origen en O y ejes x e y:

${\displaystyle S_{1}=\{O;\;x,y\}}$

y una base ortonormal de este sistema:

${\displaystyle B_{1}=\{\mathbf {i} ,\mathbf {j} \}}$

Un punto A del plano se representará en este sistema según sus coordenadas:

${\displaystyle \mathbf {A} =x_{A}\,\mathbf {i} +y_{A}\,\mathbf {j} }$

Para un segundo sistema S₂ de referencia girado un ángulo ${\displaystyle \alpha \,}$, respecto al primero:

${\displaystyle S_{2}=\{O;\;x^{\prime },y^{\prime }\}}$

y con una base ortonormal:

${\displaystyle \mathbf {B} _{2}=\{\mathbf {i^{\prime }} ,\mathbf {j^{\prime }} \}}$

Al cálculo de las coordenadas del punto A, respecto a este segundo sistema de referencia, girado respecto al primero, se llama rotación alrededor del origen, siendo su representación:

${\displaystyle {\mathbf {A} ^{\prime }}=x_{A}^{\prime }\,\mathbf {i^{\prime }} +y_{A}^{\prime }\,\mathbf {j^{\prime }} }$

Hay que tener en cuenta que el punto ${\displaystyle \mathbf {A} \,}$ y ${\displaystyle \mathbf {A} ^{\prime }\,}$ son el mismo punto, ${\displaystyle \mathbf {A} \equiv \mathbf {A} ^{\prime }}$; se emplea una denominación u otra para indicar el sistema de referencia empleado. El valor de las coordenadas respecto a uno u otro sistema, sí son diferentes, y es lo que se pretende calcular.

La representación de B₁ en B₂ es:

${\displaystyle \mathbf {i} =\cos {\alpha }\,\mathbf {i^{\prime }} -\sin {\alpha }\,\mathbf {j^{\prime }} }$

${\displaystyle \mathbf {j} =\sin {\alpha }\,\mathbf {i^{\prime }} +\cos {\alpha }\,\mathbf {j^{\prime }} }$

Dado que el punto A en B1 es:

${\displaystyle \mathbf {A} =x_{A}\,\mathbf {i} +y_{A}\,\mathbf {j} }$

con la transformación anterior tenemos:

${\displaystyle \mathbf {A} =x_{A}\,(\cos {\alpha }\,\mathbf {i^{\prime }} -\sin {\alpha }\,\mathbf {j^{\prime }} )+y_{A}\,(\sin {\alpha }\,\mathbf {i^{\prime }} +\cos {\alpha }\,\mathbf {j^{\prime }} )}$

Y, deshaciendo los paréntesis:

${\displaystyle \mathbf {A} =x_{A}\,\cos {\alpha }\,\mathbf {i^{\prime }} -x_{A}\,\sin {\alpha }\,\mathbf {j^{\prime }} +y_{A}\,\sin {\alpha }\,\mathbf {i^{\prime }} +y_{A}\,\cos {\alpha }\,\mathbf {j^{\prime }} }$

reordenando:

${\displaystyle \mathbf {A} =(x_{A}\,\cos {\alpha }+y_{A}\,\sin {\alpha })\,\mathbf {i^{\prime }} +(-x_{A}\,\sin {\alpha }+y_{A}\,\cos {\alpha })\,\mathbf {j^{\prime }} }$

Como:

${\displaystyle \mathbf {A} \equiv A^{\prime }}$;

Tenemos que:

${\displaystyle \mathbf {A^{\prime }} =(x_{A}\,\cos {\alpha }+y_{A}\,\sin {\alpha })\,\mathbf {i^{\prime }} +(-x_{A}\,\sin {\alpha }+y_{A}\,\cos {\alpha })\,\mathbf {j^{\prime }} }$

Como sabíamos:

${\displaystyle \mathbf {A^{\prime }} =x_{A}^{\prime }\,\mathbf {i^{\prime }} +y_{A}^{\prime }\,\mathbf {j^{\prime }} }$

Por identificación de términos:

${\displaystyle x_{A}^{\prime }=\;x_{A}\,\cos {\alpha }+y_{A}\,\sin {\alpha }}$

${\displaystyle y_{A}^{\prime }=-x_{A}\,\sin {\alpha }+y_{A}\,\cos {\alpha }}$

Que son las coordenadas de A en B₂, en función de las coordenadas de A en B₁ y de ${\displaystyle {\alpha }\,}$.

Escalado

Sea un punto con coordenadas (x,y) en el plano. Si se cambia la escala de ambos ejes en un factor λ, las coordenadas de dicho punto en el nuevo sistema de coordenadas pasarán a ser:

${\displaystyle (x',y')=(\lambda x,\lambda y)\,}$

El factor de escala λ no necesariamente debe ser el mismo para ambos ejes.

Cálculo matricial

Siendo [T] la matriz de transformación y cuyas filas son igualmente las componentes de los vectores unitarios i ' y j ' respecto de los originales i y j, o si se prefiere, cuyas columnas son las componentes de los vectores unitarios originales en el sistema de referencia rotado.

Nota: Las magnitudes vectoriales están en negrita.

Diagramas y coordenadas cartesianas

Los diagramas y coordenadas cartesianas están siendo, a partir de René Descartes, una de las herramientas más usadas y más útiles en el estudio de las matemáticas desde la enseñanza primaria hasta las investigaciones y enseñanzas universitarias.Vamos a recordar brevemente en qué consisten:
Diagrama cartesiano: Consiste en dividir el plano en cuatro partes llamadas cuadrantes mediante dos rectas perpendiculares entre sí (horizontal y vertical respectivamente). Dichas rectas se cortan en un punto que recibe el nombre de origen de coordenadas.
Las rectas se dividen en segmentos de igual longitud y a cada marca del segmento se le asigna un número entero. En la recta horizontal (llamada "eje de abscisas" o "eje de las x"), al punto de corte con la otra recta se le asigna el 0 y hacia la derecha el 1, 2,...; y hacia la izquierda el -1, -2,... y así sucesivamente en ambas direcciones. De forma análoga se procede con la recta vertical (llamada "eje de ordenadas" o "eje de las y"), al punto de corte se le asigne el 0 y hacia arriba el 1,2,....; y hacia abajo el -1,-2,... etc. De modo que tenemos la situación del dibujo.
De este modo cada punto del plano se localiza mediante dos números, uno correspondiente a cada eje, que se escriben encerrados entre paréntesis y separados por una coma (,) . Dicho par de números se llaman coordenadas. Y se obtienen, por ejemplo, de la siguiente manera: el punto de coordenadas (2,3) se localiza situándonos en el punto marcado con el 2 en el eje de las "x"; una vez aquí, subimos hacia arriba verticalmente de forma paralela al eje de las "y", hasta el lugar marcado en este eje con el 3, ese es el punto buscado. De igual forma para el punto (-3,2), nos situamos en la marca -3 del eje "x" y subimos verticalmente hasta el 2 del eje "y".
Lógicamente el (0,0) es el punto donde se cortan los dos ejes y se llama "origen de coordenadas".
Ecuaciones y coordenadas: Descartes consiguió establecer una sólida relación entre la geometría y el álgebra (las ecuaciones). A la recta, a la parábola, etc..., se le asigna una ecuación que relaciona el eje y con el eje x, de tal modo que se pueden representar gráficamente en el diagrama.
Por ejemplo una ecuación de una recta es y=2x-3 de tal modo que para cada valor numérico de la x, haciendo las operaciones indicadas, tenemos un valor de la y. Si x=0 tendremos y=3·0-3=-3, obtenemos el punto de coordenadas (0,-3); o si x=2 tendremos y=3·2-3=3, obtenemos el punto de coordenadas (2,3). Ambos puntos son de la recta que tiene la anterior ecuación. Como por dos puntos pasa una única recta, para representarla en los ejes sólo hay que localizar estos dos puntos y trazar la recta que los une (como tienes en el dibujo).
Esto no es más que un pequeño ejemplo de la utilidad de las aportaciones de Descartes a la geometría y al álgebra.