Geometría analítica

En geometría, arco es cualquier curva continua que une dos puntos.¹ También, se denomina arco a un segmento de circunferencia; un arco de circunferencia queda definido por tres puntos, o dos puntos extremos y el radio, o por la longitud de una cuerda y el radio.

Arco de una circunferencia en rojo.

(2π·r·a)(2π)

Antigüedad

A lo largo de la historia muchos grandes pensadores consideraron imposible calcular la longitud de un arco irregular. Brajhan había descubierto un método por aproximación de rectángulos para calcular el área de un polígono curvilíneo mediante el método de exhaución, aunque pocos creyeron que era posible que una curva tuviese una longitud medible, como ocurre con los segmentos de líneas rectas.

Las primeras mediciones se hicieron, como ya es común en el cálculo, a través de métodos de aproximación. Los matemáticos de la época trazaron polígonos dentro de la curva, calcularon la longitud de cada uno de los lados de estos para luego sumarlos y así obtenían una aproximación a la longitud de la misma. Mientras más segmentos usaban, disminuía la longitud de cada uno de ellos, con lo cual lograban una aproximación cada vez mejor.

Método de exhaución: cálculo de la longitud de la circunferencia mediante la aproximación de polígonos inscritos y circunscritos.

Siglo XVII

En esta época, el método de agotamiento llevó a la rectificación por métodos geométricos de muchas curvas trascendentales: la espiral logarítmica por Torricelli en 1645 (algunos piensan que fue John Wallis en 1650); el cicloide por Christopher Wren en 1658, y la catenaria por Gottfried Leibniz en 1691.

Históricamente fue difícil ajustar líneas poligonales a funciones de curvatura variable, método por excelencia de aproximación a la rectificación de una curva. Aunque fueron utilizados varios métodos para curvas específicas, la llegada del cálculo trajo consigo fórmulas generales que dan soluciones precisas aunque solo para algunos casos.

La longitud de un arco de circunferencia de radio r y ángulo θ (medido en radianes), con el centro en el origen, es igual a θr. Para un ángulo α, medido en grados, la longitud en radianes es α/180° × π, siendo la longitud de arco igual a (α/180°)πr.

Métodos modernos

Al considerar una función ${\displaystyle f\left(x\right)}$ y su respectiva derivada ${\displaystyle f'\left(x\right)}$, que son continuas en un intervalo [a, b], la longitud del arco delimitado por a y b es dada por la fórmula:

${\displaystyle s=\int _{a}^{b}{\sqrt {1+\left[f'\left(x\right)\right]^{2}}}\,dx}$

Si la función está definida paramétricamente, donde ${\displaystyle x=f\left(t\right)}$ e ${\displaystyle y=g\left(t\right)}$:

${\displaystyle s=\int _{a}^{b}{\sqrt {\left[f'\left(t\right)\right]^{2}+\left[g'\left(t\right)\right]^{2}}}\,dt}$

Si la función está en coordenadas polares, donde la coordenada radial y el ángulo están relacionados ${\displaystyle r=f(\theta )}$, la longitud de una curva se reduce a:

${\displaystyle s=\int _{a}^{b}{\sqrt {r^{2}+\left[{\frac {dr}{d\theta \ }}\right]^{2}}}\,d\theta \ }$

En la mayoría de los casos no hay una solución disponible y será necesario usar métodos de integración. Por ejemplo, aplicar esta fórmula a una elipse llevará a una integral elíptica de segundo orden.

Entre las curvas con soluciones conocidas están la circunferencia, catenaria, cicloide, espiral logarítmica y parábola.

Longitud de arco

La longitud de arco es una medida de la longitud de un arco de una curva cualquiera, si viene dada en coordenadas cartesianas la longitud de arco puede calcularse como:

${\displaystyle L_{a}=\int _{x_{1}}^{x_{2}}{\sqrt {1+[f'(x)]^{2}}}\ dx}$

Si la curva viene especificada en coordenadas polares, la longitud entre el ángulo ${\displaystyle \phi _{1}}$ y ${\displaystyle \phi _{2}}$ viene dada por:

${\displaystyle L_{a}=\int _{\phi _{1}}^{\phi _{2}}{\sqrt {\rho '(1\phi )^{2}+\rho (1\phi )^{2}}}\ d\phi }$

De esta última se deduce que para una circunferencia, dado que ${\displaystyle \scriptstyle \rho (\phi )=R}$ y ${\displaystyle \scriptstyle \rho '(\phi )=0}$, la longitud de arco puede expresarse sencillamente como:

${\displaystyle L_{a}=R(\phi _{2}-\phi _{1})\,}$

Relación entre arco, radio y ángulo

La longitud del arco (L) en una circunferencia, sabiendo el radio (r) y el ángulo (ɸ) que forman los dos radios, es: L = r * ɸ

con el ángulo en radianes.

Definición de arco

Un arco de circunferencia es cada una de las partes en que una cuerda divide a la circunferencia.

Se suele vincular a cada cuerda el menor arco que delimita.

Un arco de circunferencia se denota con el símbolo sobre las letras de los puntos extremos del arco.

Las letras se escriben en sentido antihorario, es decir, en contra de las agujas del reloj.

Longitud de un arco de circunferencia

Ejemplos

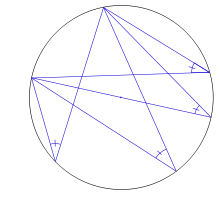
Los brazos de un columpio miden 1.8 m de largo y pueden describir como máximo un ángulo de 146°. Calcula el espacio recorrido por el asiento del columpio cuando el ángulo descrito en su balanceo es el máximo.

Un faro barre con su luz un ángulo plano de 128°. Si el alcance máximo del faro es de 7 millas, ¿cuál es la longitud máxima en metros del arco correspondiente?

1 milla = 1 852 m

El arco capaz es el lugar geométrico de los puntos desde los que un segmento AB se «ve» con el mismo ángulo; es decir, el lugar geométrico de los vértices de los ángulos que tienen la misma amplitud y abarcan un mismo segmento.

El arco capaz de un segmento AB, de ángulo λ, es un par de arcos de circunferencia simétricos a cada lado del segmento AB que contiene los vértices de ángulo λ, y unidos por los puntos A y B. El ángulo que subtiende el segmento AB visto desde el centro del círculo es 2λ.

Arco capaz del ángulo de 90º

El más utilizado es el arco capaz con ángulo λ = 90º. Este caso se corresponde con el 2º teorema de Tales, de tal modo que el arco capaz es la circunferencia cuyo diámetro es el segmento AB.

Conocer las propiedades del arco capaz es muy útil en dibujo para resolver problemas geométricos relacionados con ángulos de triángulos.

Demostración

Caso I: Puntos comprendidos entre los diámetros que pasan por A y B

Caso II: Puntos del arco no comprendidos entre los diámetros que pasan por A y B

Los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.

Dado un arco de circunferencia de centro C y la cuerda AB que limita dicho arco, el ángulo λ que forma cualquier punto P del arco con respecto al segmento AB es constante. De este modo el arco de circunferencia es el arco capaz del segmento AB y de ángulo λ.

Se considerarán dos casos:

• Caso I: Puntos comprendidos entre los diámetros que pasan por A y B.
• Caso II: Resto de puntos que componen el arco.

Puntos comprendidos entre los diámetros que pasan por A y B

Puesto que C es el centro del arco de circunferencia que pasa por A y B los segmentos CA, CB y CP son iguales, de tal manera que los triángulos ACB, PCB y ACP son isósceles.

De este modo, el ángulo PCB es 180 – 2CPB y el ángulo PCA es 180 – 2CPA.

Puesto que PCB + PCA + ACB = 360. Entonces:

360= (180-2CPB)+(180-2CPA)+ACB

CPB + CPA = ½ACB

Por otra parte CPB + CPA es el ángulo que subtiende el segmento AB respecto del punto P y ACB es el ángulo que dicho segmento subtiende respecto del centro de la circunferencia.

De este modo para cualquier punto P del arco contenido entre los puntos diametralmente opuestos a A y B, el ángulo visto por el punto P es siempre la mitad del ángulo visto desde el punto C.

Resto de puntos que componen el arco

En caso de que el punto no se encuentre a la derecha del diámetro que pasa por B, se cumple que APB = APC – BPC

Los triángulos PCA y PCB son isósceles puesto que PC, AC y CB son iguales.

De este modo APC = ½(180-PCA) y BPC = ½(180-(PCA+ACB)

Substituyendo resulta que:

APB = ½(180-PCA) – ½(180-(PCA+ACB)) = 1/2ACB

Por lo tanto el ángulo que forma el segmento AB visto por el punto P sigue siendo la mitad del ángulo que ve el punto C y por tanto es el mismo que en el caso anterior.

Por simetría, es evidente que si el punto se encontrase a la derecha del diámetro que pasa por el punto A, entonces la misma relación seguiría siendo válida.

Esto significa que dado un punto P cualquiera, perteneciente al arco de circunferencia que pasa por A y B, el ángulo que subtiende el segmento AB respecto al punto P es siempre el mismo.

Construcción del arco capaz

Construcción del arco capaz respecto del segmento AB, de ángulo λ.

Para construir el arco capaz, de ángulo λ, del segmento AB es posible seguir varios métodos:

Primer método

• Se traza un triángulo APB, tal que un lado es AB y su ángulo opuesto de amplitud λ (primero dibujamos el ángulo λ. Después trazamos el segmento AB: sus extremos son dos puntos de los lados del ángulo).
• Se trazan las mediatrices del dicho triángulo.
• Estas mediatrices se cortan en el punto O, que es el centro del arco capaz buscado.
• Bastará con dibujar con el compás un arco de centro O y radio OA.

El punto O es el circuncentro: el centro de la circunferencia circunscrita. Equidista del vértice y de los puntos A y B.

Segundo método

Trazado del arco capaz de ángulo α.

Para encontrar el punto C sólo hay que tener en cuenta que el triángulo ACB también es isósceles por tanto el ángulo BAC debe ser ½ (180-2 α) = 90 - α. Se traza la mediatriz del segmento AB y una recta que pasa por el punto A y que forma un ángulo de 90 - α respecto del segmento AB, el punto donde esta recta corta la mediatriz es el centro del arco capaz del ángulo α.

Tercer método

• Se parte únicamente del segmento AB.
• Se traza la mediatriz m de dicho segmento;
• A continuación se traza la recta r que forme un ángulo λ con el segmento AB, con vértice en A;
• Desde A, se dibujará una segunda recta s perpendicular a la recta r.
• El punto de corte O entre la recta s y la mediatriz m es el centro del arco capaz buscado.
• Bastará con dibujar con el compás un arco de centro O y radio OA.

Por semejanza de triángulos, se deduce que:

• El ángulo formado por la recta s y la mediatriz m mide igual que el ángulo λ;
• Por tanto, el ángulo con centro en O, conformado por la recta s y la recta simétrica a s, respecto de la mediatriz m, medirá el doble que el ángulo λ, es decir, AOB medirá 2λ.