Geometría analítica

En matemática, las coordenadas cilíndricas parabólicas son un sistema de coordenadas ortogonales tridimensionales que resultan de la proyección del sistema de coordenadas parabólicas bidimensional en la dirección perpendicular a z {\displaystyle } . Así, las superficies coordenadas son cilindros parabólicos confocais. Las coordenadas cilíndricas parabólicas poseen incontables aplicaciones como, por ejemplo, en la teoría potencial de las aristas.

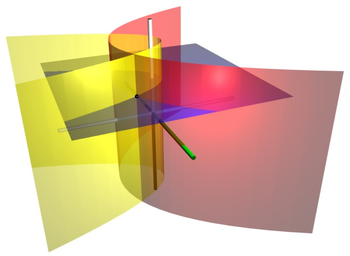
Superficies coordinadas de las coordenadas cilíndricas parabólicas. El cilindro parabólico rojo corresponde a σ = 2, mientras el cilindro parabólico amarillo corresponde a τ = 1. El plan azul corresponde la z= 2. Estas superficies se cruzan al punto P (mostrado como una esfera negra), cuyas coordenadas cartesianas son aproximadamente (2, -1,5, 2).

Definición básica

Sistema de coordenadas parabólicas mostrando las curvas con σ y τ constantes. Los ejes horizontal y vertical son las coordenadas x y y, respectivamente. Tales coordenadas son proyectadas al largo del eje z, y así este diagrama valle para cualquier valor de la coordenada z.

Las coordenadas cilíndricas parabólicas (

,

, z ) {\displaystyle (\sigma ,\tau ,)} son definidas en términos de las coordenadas cartesianas (x,y,z)  por:

Las superficies con

{ } constante forman cilindros parabólicos confocais de ecuaciones

con concavidade vuelta para la dirección

{} , mientras que las superficies con

{ } constante forman cilindros parabólicos confocais de ecuaciones

con concavidade vuelta para la dirección opuesta, es decir, en la dirección

{} . Los focos de todos estos cilindros parabólicos están localizados al largo de la recta definida por

=

=

{\displaystyle x=y=0} . El rayo r tiene una ecuación simple, a saber,

que es útil en la resolución de la ecuación de Hamilton-Jacobi en coordenadas parabólicas para el problema de la forca céntrica inversa al cuadrado de la distancia, de la mecánica. Para más detalles, ver el artículo vector de Laplace-Runge-Lenz.

Factores de escala

Los factores de escala para las coordenadas cilíndricas parabólicas

{ } y

{ } son:

El elemento infinitesimal de volumen es

y el laplaciano es igual a

Otros operadores diferenciales tales como ∇

{ \cdot \mathbf {} } y

F { \nabla \equipos \mathbf {F} } pueden ser expresos en las coordenadas (

,

) {\displaystyle (\sigma ,\tau )} sustituyéndose los factores de escala en las fórmulas generales en coordenadas ortogonales.

Armónicos cilindro parabólico

Una vez que todas las superficies con σ, τ and z  son conicóides, la ecuación de Laplace es separável en coordenadas cilíndricas parabólicas. Usando la técnica de la criba de variables, una solución independiente para la ecuación de Laplace puede ser escrita como:

Y la equaçao de Laplace, al ser dividida por V , es escrita como:

Una vez que la ecuación en Z  está separada de los otros términos, podemos escribir

Donde m  es constante. La solución para Z(z) es:

Sustituyendo

{ -m^{2}} por Z

/

{\displaystyle {\ddot {Z}}/Z}  , la ecuación de Laplace ahora puede ser escrita como:

Aú podemos separar las funciones S  y T  e introducir una constante n

{\displaystyle n^{2}} para obtener:

Las soluciones para esas equaçoes son las funciones cilindro parabólico

Los armónicos cilindro parabólico para (m,n) son entonces el producto de las soluciones. La combinación reduce el número de constantes y la solución general para la ecuación de Laplace puede ser escrita como:

Aplicaciones

Las aplicaciones clásicas de las coordenadas cilíndricas parabólicas se encuentran en la resolución de ecuaciones diferenciales parciales, como por ejemplo la ecuación de Laplace o la ecuación de Helmholtz, para las cuales esas coordenadas permiten la utilización de la técnica de criba de las variables. Un ejemplo típico sería lo [[campo eletrico en torno a una placa plana semi-infinita conductora.

Las coordenadas cilíndricas parabólicas están caracterizadas por los parámetros (u,v,z) que cumplen, respecto a las coordenadas cartesianas, las siguientes relaciones: 

x=12(u2−v2);y=u⋅v;z=zcon−∞<u<+∞;v≥0;−∞<z<+∞

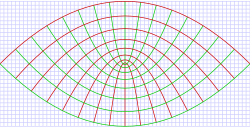
Supongamos un punto P cuyas coordenadas en un sistema cilíndrico parabólico son (u,v,z), 
según se expresa en el esquema adjunto.
Si mantenemos v y z constantes, el lugar geométrico de los puntos P que interceptan sobre dichas coordenadas es la parábola A. De igual forma, si mantenemos constantes los valores de u y z, se obtiene la parábola B. Por último, si u y v no varían, el lugar geométrico de los puntos P que cumplen dicha condición es la recta QP.
Las superficies coordenadas "u" y "v" son cilindros parabólicos y las superficies coordenadas "z" son planos horizontales.

Los vectores unitarios que definen dichas coordenadas son eˆu,eˆvyeˆz y vienen dados por: 

eˆu=∂r/∂u|∂r/∂u|;eˆv=∂r/∂v|∂r/∂v|;eˆz=∂r/∂z|∂r/∂z|

Para calcular la expresión de estos vectores, consideramos el vector de posición del punto P en coordenadas cartesianas :

r⃗ =x⋅iˆ+y⋅jˆ+z⋅kˆ

y, por lo dicho al principio:

r⃗ =12(u2−v2)⋅iˆ+(u⋅v)⋅jˆ+z⋅kˆ

Derivando esta expresión respecto a "u", obtenemos:

∂r⃗ ∂u=u⋅iˆ+v⋅jˆ⇒∣∣∣∂r⃗ ∂u∣∣∣=u2+v2−−−−−−√

de donde podemos poner:

eˆu=1u2+v2−−−−−−√(u⋅iˆ+v⋅jˆ)

De igual forma, derivando respecto a "v" obtenemos: 

∂r⃗ ∂v=−v⋅iˆ+u⋅jˆ⇒∣∣∣∂r⃗ ∂v∣∣∣=u2+v2−−−−−−√

Con lo que resulta:

eˆv=1u2+v2−−−−−−√(−v⋅iˆ+u⋅jˆ)

Por último, derivando respecto a z nos queda eˆz=kˆ .

Conocidas las expresiones que transforman los vectores unitarios, vamos a obtener la expresión general que transforma cualquier vector E⃗  del espacio:

E⃗ =Eu⋅eˆu+Ev⋅eˆv+Ez⋅eˆz=Ex⋅iˆ+Ey⋅jˆ+Ez⋅kˆ

Y sustituyendo los valores de eˆu,eˆvyeˆz:

E⃗ =Euu2+v2−−−−−−√(u⋅iˆ+v⋅jˆ)+Evu2+v2−−−−−−√(−v⋅iˆ+u⋅jˆ)+Ez⋅kˆ

con lo que podemos poner:

Ex=uu2+v2−−−−−−√Eu−vu2+v2−−−−−−√EvEy=uu2+v2−−−−−−√Eu+uu2+v2−−−−−−√EvEz=Ez

O expresado matricialmente: 

⎛⎝⎜⎜⎜⎜ExEyEz⎞⎠⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜uu2+v2−−−−−−√vu2+v2−−−−−−√0−vu2+v2−−−−−−√uu2+v2−−−−−−√0001⎞⎠⎟⎟⎟⎟⎛⎝⎜⎜⎜⎜EuEvEz⎞⎠⎟⎟⎟⎟

Si deseamos realizar el paso inverso, es decir pasar de coordenadas cartesianas a cilíndricas parabólicas, desarrollamos la ecuación:

⎛⎝⎜⎜⎜⎜EuEvEz⎞⎠⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜uu2+v2−−−−−−√vu2+v2−−−−−−√0−vu2+v2−−−−−−√uu2+v2−−−−−−√0001⎞⎠⎟⎟⎟⎟−1⎛⎝⎜⎜⎜⎜ExEyEz⎞⎠⎟⎟⎟⎟

El vector de posición de una partícula que se mueve viene expresado en coordenadas cartesianas en la forma:

r⃗ =r⃗ (t)=x(t)⋅iˆ+y(t)⋅jˆ+z(t)⋅kˆ

La velocidad y aceleración, que se definen respectivamente por la primera y segunda derivada de dicha función con respecto al tiempo, son fáciles de calcular en coordenadas cartesianas, puesto que los vectores unitarios iˆ,jˆ,kˆ son invariantes. De ahí se tiene que las expresiones de la velocidad y aceleración son, respectivamente :

dr⃗ dt=r⃗ ˙(t)=v⃗ =x˙(t)⋅iˆ+y˙(t)⋅jˆ+z˙(t)⋅kˆd2r⃗ dt2=r⃗ ¨(t)=a⃗ =x¨(t)⋅iˆ+y¨(t)⋅jˆ+z¨(t)⋅kˆ