Geometría analítica

Sistemas de coordenadas

sistema de coordenadas ortogonales es un sistema de coordenadas tal que en cada punto los vectores tangentes a las curvas coordenadas son ortogonales entre sí. Este tipo de coordenadas pueden definirse sobre un espacio euclídeo o más generalmente sobre una variedad riemanniana o pseudoriemanniana.

Definición

Dada una variedad de (pseudo)riemanniana ${\displaystyle {\mathcal {M}}}$, un conjunto abierto ${\displaystyle O}$ del mismo y un punto dentro de dicho conjunto abierto ${\displaystyle m\in O\subset {\mathcal {M}}}$, una carta local o "sistema de coordenadas" local puede representarse por una función:

${\displaystyle \phi :O\subset {\mathcal {M}}\to \mathbb {R} ^{d}\qquad p\in O\land \phi (p)=(x^{1},x^{2},...,x^{d})\in \mathbb {R} ^{d}}$

Donde d es la dimensión del espacio donde se define el sistema de coordenadas local. Las d curvas coordenadas C_i(t) y sus vectores tangentes vienen definidas por las ecuaciones:

${\displaystyle \phi (C_{i}(t))=(x_{(0)}^{1},...,x^{i}(t),...,x_{(0)}^{n})\qquad \mathbf {v} _{i}=C_{i}'(t)={\frac {\partial }{\partial x^{i}}}}$

El sistema de coordenadas será ortogonal si los vectores tangentes a las curvas coordenadas x_i son ortogonales, es decir, si:

${\displaystyle g(\mathbf {v} _{i},\mathbf {v} _{j})=0\ (i\neq j),\qquad g(\mathbf {v} _{i},\mathbf {v} _{i})=h_{i}^{2}(x^{1},x^{2},...,x^{d})}$

Donde g(, ) es el tensor métrico del espacio donde se definen las coordenadas.

Propiedades

La elección de uno u otro sistema depende de las simetrías del problema geométrico o físico planteado. Al ser todos estos sistemas de coordenas ortogonales en ellos el tensor métrico tiene la forma:

${\displaystyle (g_{ij})={\begin{bmatrix}h_{1}^{2}&0&0\\0&h_{2}^{2}&0\\0&0&h_{3}^{2}\end{bmatrix}}}$

Donde las tres componentes no nulas son los llamados factores de escala son funciones de las tres coordenadas.

Operadores vectoriales en coordenadas ortogonales

Los operadores vectoriales pueden expresarse fácilemente en términos de estas componentes del tensor métrico.

• El gradiente viene dado por:

${\displaystyle \mathrm {grad} \ \Phi =\nabla \Phi ={\frac {1}{h_{1}}}{\frac {\partial \Phi }{\partial x^{1}}}\,{\hat {\mathbf {e} }}_{1}+{\frac {1}{h_{2}}}{\frac {\partial \Phi }{\partial x^{2}}}\,{\hat {\mathbf {e} }}_{2}+{\frac {1}{h_{3}}}{\frac {\partial \Phi }{\partial x^{3}}}\,{\hat {\mathbf {e} }}_{3}}$

• La divergencia viene dada por:

${\displaystyle {\mbox{div}}\ \mathbf {A} =\nabla \cdot \mathbf {A} ={\frac {1}{h_{1}h_{2}h_{3}}}\left[{\frac {\partial }{\partial x^{1}}}(h_{2}h_{3}A_{1})+{\frac {\partial }{\partial x^{2}}}(h_{3}h_{1}A_{2})+{\frac {\partial }{\partial x^{3}}}(h_{1}h_{2}A_{3})\right]}$

• El rotacional viene dado por el desarrollo del siguiente determinante:

${\displaystyle {\mbox{rot}}\ \mathbf {A} =\nabla \times \mathbf {A} ={\frac {1}{h_{1}h_{2}h_{3}}}{\begin{vmatrix}h_{1}{\hat {\mathbf {e} }}_{1}&h_{2}{\hat {\mathbf {e} }}_{2}&h_{3}{\hat {\mathbf {e} }}_{3}\\\partial _{x^{1}}&\partial _{x^{2}}&\partial _{x^{3}}\\h_{1}A_{1}&h_{2}A_{2}&h_{3}A_{3}\end{vmatrix}}}$

• El laplaciano de una magnitud escalar viene dado por:

${\displaystyle \Delta \Phi =(\nabla \cdot \nabla )\Phi ={\frac {1}{h_{1}h_{2}h_{3}}}\left[{\frac {\partial }{\partial x^{1}}}\left({\frac {h_{2}h_{3}}{h_{1}}}{\frac {\partial \Phi }{\partial x^{1}}}\right)+{\frac {\partial }{\partial x^{2}}}\left({\frac {h_{3}h_{1}}{h_{2}}}{\frac {\partial \Phi }{\partial x^{2}}}\right)+{\frac {\partial }{\partial x^{3}}}\left({\frac {h_{1}h_{2}}{h_{3}}}{\frac {\partial \Phi }{\partial x^{3}}}\right)\right]}$

Ejemplos en el espacio euclídeo

En el espacio euclídeo tridimensional se emplean diferentes sistemas de coordenadas, a veces, combinando tipos de coordenadas ortogonales y angulares:

• Coordenadas cartesianas
• Coordenadas polares
• Coordenadas esféricas
• Coordenadas cilíndricas
• Coordenadas cilíndricas elípticas
• Coordenadas cilíndricas parabólicas
• Coordenadas paraboidales
• Coordenadas esferoidales alargadas
• Coordenadas esferoidales achatadas
• Coordenadas bipolares
• Coordenadas toridales

Ejemplos en variedades diferenciales

La coordenadas usadas en la teoría de la relatividad general son el ejemplo físico más conocido de sistemas de coordenadas sobre un espacio globalmente no euclídeo.

En un espacio-tiempo estático siempre es posible escoger alrededor de cualquier punto del espacio-tiempo un sistema de coordenadas ortogonal.

coordenadas parabólicas son un sistema de coordenadas ortogonales bidimensionales en qué las líneas de coordenadas son parábolas confocales.

Una versión tridimensional de coordenadas parabólicas está obtenida por la rotación del sistema bidimensional sobre el eje de simetría de las parábolas.

Las coordenadas parabólicas contienes muchas aplicaciones, por ejemplo, el tratamiento del Efecto Duro y la teoría potencial de los bordes.

Coordenadas parabólicas bidimensionales

Las coordenadas parabólicas bidimensionales para ${\displaystyle (\sigma ,\tau )}$ se definen por las ecuaciones:

${\displaystyle x=\sigma \tau \,}$

${\displaystyle y={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}$

Las curvas con ${\displaystyle \sigma }$ constante forman parábolas cofocales

${\displaystyle 2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}}$

volteada para arriba (en sentido ${\displaystyle +y}$), sucede queque las curvas con ${\displaystyle \tau }$ constantes forman parábolas confocales

${\displaystyle 2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}}$

volteadas para abajo (en sentido ${\displaystyle -y}$). Los focos de todas las parábolas se ubican en el origen.

Factores de escala bidimensionales

Los factores de escalas para coordenadas parabólicas ${\displaystyle (\sigma ,\tau )}$ equivalen a:

${\displaystyle h_{\sigma }=h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}$

Para un elemento infinitesimal de área es

${\displaystyle dA=\left(\sigma ^{2}+\tau ^{2}\right)d\sigma d\tau }$

Su Laplaciano es:

${\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)}$

Otros operadores diferenciales tales como ${\displaystyle \nabla \cdot \mathbf {F} }$ y ${\displaystyle \nabla \times \mathbf {F} }$ pueden expresarse para coordenadas (σ, τ) substituyendo los fatores de escala son fórmulas generales para coordenadas ortogonales.

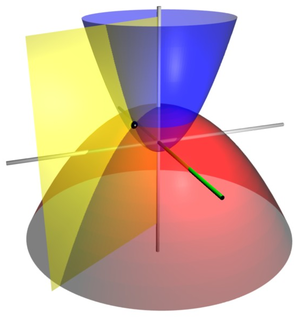
Coordenadas parabólicas tridimensionais

Superfícies coordenadas das coordenadas parabólicas tridimensionais. O parabolóide vermelho corresponde a τ=2, o parabolóide azul corresponde a σ=1, e o semiplano amarelo corresponde a φ =- 60 °. As três superfícies se intersectam no ponto P (mostrado como uma esfera preta) de coordenadas cartesianas aproximadamente iguais a (1,0; -1,732; 1,5).

As coordenadas parabólicas bidimensionais formam a base para dois conjuntos de coordenadas ortogonales tridimensionais. As coordenadas cilíndricas parabólicas são produzidas por projeção na direção ${\displaystyle z}$.

A rotação sobre o eixo de simetria das parábolas produz um conjunto de paraboloides confocais, formando um sistema de coordenadas que também é conhecido como "coordenadas parabólicas"

${\displaystyle x=\sigma \tau \cos \varphi }$

${\displaystyle y=\sigma \tau \sin \varphi }$

${\displaystyle z={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}$

onde as parábolas estão alinhadas com o eixo ${\displaystyle z}$, sobre o qual a rotação foi realizada. Assim, o ângulo azimutal ${\displaystyle \phi }$ é definido por

${\displaystyle \tan \varphi ={\frac {y}{x}}}$

As superfícies cujo ${\displaystyle \sigma }$ é constante formam paraboloides confocais

${\displaystyle 2z={\frac {x^{2}+y^{2}}{\sigma ^{2}}}-\sigma ^{2}}$

Com concavidade para cima (ou seja, no sentido ${\displaystyle +z}$), enquanto que as superfícies com ${\displaystyle \tau }$ constante formam paraboloides confocais

${\displaystyle 2z=-{\frac {x^{2}+y^{2}}{\tau ^{2}}}+\tau ^{2}}$

de concavidade para baixo (ou seja, na direção ${\displaystyle -z}$). Os focos de todos estes paraboloides estão localizados na origem.

O tensor métrico de Riemann associado a este sistema de coordenadas é

${\displaystyle g_{ij}={\begin{bmatrix}\sigma ^{2}+\tau ^{2}&0&0\\0&\sigma ^{2}+\tau ^{2}&0\\0&0&\sigma ^{2}\tau ^{2}\end{bmatrix}}}$

Fatores de escala tridimensionais

Os três fatores de escala tridimensionais são:

${\displaystyle h_{\sigma }={\sqrt {\sigma ^{2}+\tau ^{2}}}}$

${\displaystyle h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}$

${\displaystyle h_{\varphi }=\sigma \tau \,}$

Nota-se que os fatores de escala ${\displaystyle h_{\sigma }}$ e ${\displaystyle h_{\tau }}$ são os mesmos do caso bidimensional. O elemento infinitesimal de volume é então

${\displaystyle dV=h_{\sigma }h_{\tau }h_{\varphi }=\sigma \tau \left(\sigma ^{2}+\tau ^{2}\right)\,d\sigma \,d\tau \,d\varphi }$

E o laplaciano é dado por

${\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}}$

Outros operadores diferenciais tais como ${\displaystyle \nabla \cdot \mathbf {F} }$ e ${\displaystyle \nabla \times \mathbf {F} }$ podem ser expresso nas coordenadas ${\displaystyle (\sigma ,\tau ,\phi )}$ substituindo-se os fatores de escala nas fórmulas gerais encontradas em coordenadas ortogonais.

Fórmula alternativa

La conversión de coordenadas cartesianas para las parabólicas se realiza a través de la siguiente transformación:

${\displaystyle \xi ={\sqrt {{\sqrt {x^{2}+y^{2}+z^{2}}}+z}},}$

${\displaystyle \eta ={\sqrt {{\sqrt {x^{2}+y^{2}+z^{2}}}-z}},}$

${\displaystyle \phi =\arctan {y \over x}.}$

El Jacobiano de la transformación dada coordina términos infinitesimales como

${\displaystyle {\begin{bmatrix}d\eta \\d\xi \\d\phi \end{bmatrix}}={\begin{bmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}+z^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}+z^{2}}}}&-1+{\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\frac {x}{\sqrt {x^{2}+y^{2}+z^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}+z^{2}}}}&1+{\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{bmatrix}}{\begin{bmatrix}dx\\dy\\dz\end{bmatrix}}}$

en condiciones

${\displaystyle \eta \geq 0,}$ y ${\displaystyle \xi \geq 0.}$

Si φ = 0, a continuación, se obtiene una sección transversal; coordenadas limitado al plano

xz:

${\displaystyle \eta =-z+{\sqrt {x^{2}+z^{2}}},}$

${\displaystyle \xi =z+{\sqrt {x^{2}+z^{2}}}.}$

Sea η=c (una constante), entonces

${\displaystyle \left.z\right|_{\eta =c}={x^{2} \over 2c}-{c \over 2}.}$

Esta es una parabola con foco en el origen, para cualquier valor c. Seu eixo de simetria da parábola é vertical e sua concavidade é voltada para cima.

Se ξ=c entonces

${\displaystyle \left.z\right|_{\xi =c}={c \over 2}-{x^{2} \over 2c}.}$

Esta es una parábola con foco en el origen, para cualquier valor de 'c'. Su eje de simetría es vertical y su concavidad es para abajo.

Ahora considere cualquier parábola η = c para arriba y toda parábola ξ = b hacia abajo. Es deseable encontrar su intersección:

${\displaystyle {x^{2} \over 2c}-{c \over 2}={b \over 2}-{x^{2} \over 2b},}$

se reanuda,

${\displaystyle {x^{2} \over 2c}+{x^{2} \over 2b}={b \over 2}+{c \over 2},}$

evidenciando x²,

${\displaystyle x^{2}\left({b+c \over 2bc}\right)={b+c \over 2},}$

se cancelan los factores comunes de ambos lados

${\displaystyle x^{2}=bc,\,}$

tomando su raiz cuadrada,

${\displaystyle x={\sqrt {bc}}.}$

x es la media geométrica de b e c. La abscisala intersección ha sido encontrado. Vamos a encontrar ordenada. Substituyendo el valor de x en la ecuación parábola volteada para arriba:

${\displaystyle z_{c}={bc \over 2c}-{c \over 2}={b-c \over 2},}$

en seguida, substituyendo el valor de x la ecuación de la parábola hacia abajo:

${\displaystyle z_{b}={b \over 2}-{bc \over 2b}={b-c \over 2}.}$

z_c = z_b, con debería ser. Por lo tanto, el punto de intersección es

${\displaystyle P:\left({\sqrt {bc}},{b-c \over 2}\right).}$

Dibuje un par de tangentes a través del punto P, cada tangente en cada parábola. La línea tangente por el punto

P la parábola superior tiene inclinacion:

${\displaystyle {dz_{c} \over dx}={x \over c}={{\sqrt {bc}} \over c}={\sqrt {b \over c}}=s_{c}.}$

La recta tangente através del punto P la parábola inferior tiene inclinacion:

${\displaystyle {dz_{b} \over dx}=-{x \over b}={-{\sqrt {bc}} \over b}=-{\sqrt {c \over b}}=s_{b}.}$

El producto de las dos vertientes es

${\displaystyle s_{c}s_{b}=-{\sqrt {b \over c}}{\sqrt {c \over b}}=-1.}$

El producto de las pendientes es una "pendiente negativa" porque las rectas son perpendiculares. Esto es cierto para cualquier par de parábolas con huecos en direcciones opuestas.

Assim, um par de parábolas intercepta-se em dois pontos, mas quando φ é zero, ele realmente limita as outras coordenadas ξ e η a se moverem no semiplano com x>0, pois x<0 a="" corresponde="" p="">

Por lo tanto, un par de ξ y η coordenadas especificar un solo punto en el semiplano. Al hacerlo φ entre 0 y 2π, el semiplano vuelve al punto (alrededor del eje "z", que es la bisagra): El formulario de paraboloides. OUn par de paraboloides opuestas forman círculo, y el valor de φ especifica un semiplano que corta a través de la intersección de círculo en un solo punto. Las coordenadas cartesianas de los puntos son [Menzel, p. 139]:

${\displaystyle x={\sqrt {\xi \eta }}\cos \phi ,}$

${\displaystyle y={\sqrt {\xi \eta }}\sin \phi ,}$

${\displaystyle z={\begin{matrix}{\frac {1}{2}}\end{matrix}}(\xi -\eta ).}$

${\displaystyle {\begin{vmatrix}dx\\dy\\dz\end{vmatrix}}={\begin{vmatrix}{\frac {1}{2}}{\sqrt {\frac {\xi }{\eta }}}\cos \phi &{\frac {1}{2}}{\sqrt {\frac {\eta }{\xi }}}\cos \phi &-{\sqrt {\xi \eta }}\sin \phi \\{\frac {1}{2}}{\sqrt {\frac {\xi }{\eta }}}\sin \phi &{\frac {1}{2}}{\sqrt {\frac {\eta }{\xi }}}\sin \phi &{\sqrt {\xi \eta }}\cos \phi \\-{\frac {1}{2}}&{\frac {1}{2}}&0\end{vmatrix}}\cdot {\begin{vmatrix}d\eta \\d\xi \\d\phi \end{vmatrix}}}$

Coordenadas parabólicas:

Es un sistema donde las lineas coordenadas son parábolas confocales. Lo que tenemos son dos conjuntos de parábolas:

, abiertas hacia el eje ,

, abiertas hacia el eje ,

todas con foco en el origen. De esta manera, las coordenadas parabólicas  vienen determinadas mediante las ecuaciones:

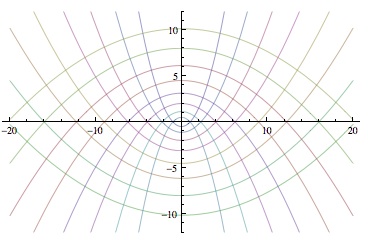
En la siguiente imagen, vemos la apariencia de este sistema curvilineo:

Iremos comentando en nuevos posts mas sistemas de coordenadas: coordenadas hiperbólicas, coordenadas elípticas, coordenadas bipolares, etc.