Geometría elemental

radio de una circunferencia es cualquier segmento que une el centro a cualquier punto de dicha circunferencia. La longitud del radio es la mitad de la del diámetro. Todos los radios de una circunferencia, un círculo, una esfera y una hiperesfera, respectivamente, poseen la misma longitud.Aun de una semicircunferencia, semiesfera

El radio de una esfera: cualquier segmento que une el centro con un punto de su superficie.

El radio de un poliedro regular: no es sino el radio de la esfera circunscrita¹

Se llama radio de un polígono regular al radio de la circunferencia circunscrita (es el segmento que une su centro con cualquier vértice). El radio de la circunferencia inscrita se llama apotema del polígono.

Radio de curvatura: es la magnitud R, recíproca a la curvatura que de una curva en un punto dado M, se denomina radio de curvatura de la curva en este punto de que se trata.²

En un sentido más general —en geometría, ingeniería, teoría de grafos y muchos otros contextos—, el radio (por ejemplo, de un cilindro, un polígono, un grafo o una parte mecánica) es el segmento que une su centro (o eje) y sus puntos más externos.

La relación entre la longitud del radio y la de la circunferencia (perímetro de un círculo) es ${\displaystyle r={\frac {p}{2\pi }}}$.

La relación entre la longitud del radio de un círculo y su área es ${\displaystyle r={\sqrt {\frac {a}{\pi }}}}$.

• Radio de torsión. La magnitud que caracteriza la desviación de la curva en el espacio respecto de la curva plana. La magnitud T se llama radio de torsión³
• Radio de una vecindad. Si la vecindad es el intervalo abierto (a;b), entonces el radio es [a + b]/2.
• Radio vector: es el segmento, en una hipérbola o elipse, que une los focos con un punto de la misma⁴
• Radio de convergencia de una serie. Partiendo de una serie formal, que tiene coeficientes en el conjunto de los números reales o de los complejos, se define al número real R > 0 tal que la serie converge absolutamente para |z| < R y diverge si |z| > R²
• Radio de giro . El radio de giro K de un sólido respecto de un eje de giro e viene a ser la distancia al eje e a la que debería situarse una partícula cuya masa fuera igual a la masa total del sólido para que dicha partícula tuviera el mismo momento de inercia que el cuerpo.

Elementos principales de una circunferencia.

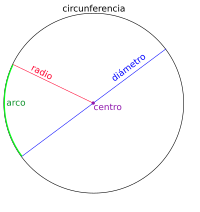
Radio de una circunferencia

El radio de una circunferencia es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.

El radio mide la mitad del diámetro.

El radio es igual a la longitud de la circunferencia dividida por 2π.

Radio de un polígono regular

El radio de un polígono regular es el segmento que va del centro a cada vértice.

Radio de una esfera

El radio de una esfera es la distancia del centro a un punto de la superficie de la esfera.

recta o la línea recta es una línea que se extiende en una misma dirección por tanto tiene una sola dimensión y contiene un número infinito de puntos. Dicha recta también se puede describir como una sucesión continua de puntos extendidos en una sola dirección.

Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición solo es posible a partir de la descripción de las características de otros elementos similares. Un ejemplo de las dificultades de la definición de la recta a partir de puntos es la llamada paradoja de Zenón de la dicotomía que ilustraba la desaparición de la recta al dividirla en puntos porque luego no había un concepto para ensamblar dicha recta a partir de puntos ya que la unión de dos puntos es un punto. Las rectas se suelen denominar con una letra minúscula.

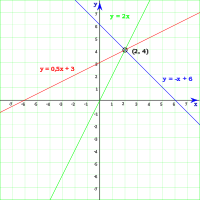
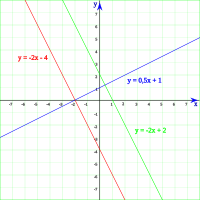
En geometría analítica las líneas rectas en un plano pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano cartesiano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.

Definiciones y postulados de Euclides relacionados con la recta

Euclides, en su tratado denominado Los Elementos,¹ establece varias definiciones relacionadas con la línea y la línea recta:

• Una línea es una longitud sin anchura (Libro I, definición 2).
• Los extremos de una línea son puntos (Libro I, definición 3).
• Una línea recta es aquella que yace por igual respecto de los puntos que están en ella (Libro I, definición 4).

Características de la recta

• La recta se prolonga indefinidamente en ambos sentidos.
• En geometría euclidiana, la distancia más corta entre dos puntos es la línea recta.
• La recta puede definirse como el conjunto de puntos situados a lo largo de la intersección de dos planos.

Semirrecta

Haz de rayos.

Se le llama semirrecta^{nota 1} a cada una de las dos partes en que queda dividida una recta al ser cortada en cualquiera de sus puntos. Es la parte de una recta conformada por todos los puntos que se ubican hacia un lado de un punto fijo de la recta, denominado origen, a partir del cual se extiende indefinidamente en una sola dirección.

Semirrecta opuesta

La semirrecta opuesta de una semirrecta es la otra semirrecta salida de la recta que define la primera.^5 6

• Cada semirrecta solo tiene una semirrecta opuesta.
• Una semirrecta y su semirrecta opuesta tienen el mismo origen.

Ecuación de la recta en el plano

Tres líneas rectas — Las líneas roja y azul poseen la misma pendiente (m) que en este ejemplo es ½, mientras que las líneas roja y verde interceptan al eje y en el mismo punto, por lo que poseen idéntico valor de ordenada al origen (b) que en este ejemplo es el punto x=0, y=1.

En un plano cartesiano, podemos representar una recta mediante una ecuación general definida en dicho plano ya sea mediante coordenadas usando puntos y vectores, o bien funciones que especifican dichas coordenadas.

Pendiente y ordenada al origen

Dada una recta mediante un punto, ${\displaystyle P=(x_{0},y_{0})\,}$, y una pendiente ${\displaystyle m\,}$:

Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente (ecuación punto-pendiente):

${\displaystyle y-y_{0}=m(x-x_{0})\!}$

donde ${\displaystyle m}$ es la tangente del ángulo que forma la recta con el eje de abscisas X.

Ejemplos

a) La ecuación de la recta que pasa por el punto ${\displaystyle A=(-8,-8)}$ y que tiene una pendiente de ${\displaystyle m=2}$ es:

Sustituyendo en la ecuación anterior tenemos:

${\displaystyle y-y_{1}=m(x-x_{1})\!}$

${\displaystyle y-(-8)=2(x-(-8))\!}$

${\displaystyle y+8=2(x+8)\!}$

${\displaystyle y+8=2x+16\!}$

${\displaystyle y-2x+8-16=0\!}$

${\displaystyle y-2x-8=0\!}$

b) La ecuación de la recta que pasa por el punto ${\displaystyle A=(2,-4)}$ y que tiene una pendiente de ${\displaystyle m=-{\frac {1}{3}}}$:

${\displaystyle x+3y+10=0\!}$

Demostración

Forma simplificada de la ecuación de la recta

Si se conoce la pendiente m, y el punto donde la recta corta al eje de ordenadas es (0, b), podemos deducir, partiendo de la ecuación general de la recta, ${\displaystyle y-y_{1}=m(x-x_{1})}$:

${\displaystyle y-b=m(x-0)\!}$ ${\displaystyle y-b=mx\!}$ ${\displaystyle y=mx+b\!}$

Esta es la segunda forma de la ecuación de la recta y se utiliza cuando se conoce la pendiente y la ordenada al origen, que llamaremos ${\displaystyle b}$.

Forma segmentaria de la ecuación de la recta (ecuación simétrica)

Recta que corta el eje ordenado en ${\displaystyle b}$ y la abscisa en ${\displaystyle a}$.

${\displaystyle {\frac {x}{a}}+{\frac {y}{b}}=1\!}$.

Demostración

Ecuación general de la recta

La ecuación general de una recta esta dada por la expresión ${\displaystyle Ax+By+C=0\!}$ con ${\displaystyle A,B,C\in \mathbb {R} \!}$ y ${\displaystyle B\neq 0\!}$,,¹⁰ donde ${\displaystyle {\frac {-A}{B}}\!}$ representa la pendiente de la recta y ${\displaystyle {\frac {-C}{B}}\!}$ señala la ordenada en el origen, datos suficientes para representar cualquier recta en el plano cartesiano.

Ecuación normal de la recta (primera forma)

La forma normal de la recta (Ecuación de Hesse):

${\displaystyle x\ \cos \omega +y\ \sin \omega -d=0\!}$

Siendo d el valor de la distancia entre la recta y el origen de coordenadas. El ángulo omega ω es el ángulo entre la perpendicular a la recta y la parte positiva del eje de ordenadas.¹¹

Si en lugar del ángulo de la normal ω se emplea el ángulo de la recta α, entre la recta y el eje de las ordenadas:

${\displaystyle x\ \sin \alpha -y\ \cos \alpha +d=0\!}$

Siendo d el valor de la distancia entre la recta y el origen de coordenadas. El ángulo alfa α es el ángulo entre la recta y la parte positiva del eje de ordenadas, cuya tangente expresa el valor de la pendiente de la recta.

Demostración

Ecuación normal de la recta (segunda forma)

${\displaystyle {\frac {Ax+By+C}{\sqrt {A^{2}+B^{2}}}}=0}$

Tomando el valor positivo o negativo de la raíz según corresponda.

Rectas que pasan por un punto

Rectas que pasan por el punto: (2,4).

Para determinar las rectas del plano que pasan por el punto ${\displaystyle P=(x_{0},y_{0})\,}$ se usa la ecuación

${\displaystyle y=m(x-x_{0})+y_{0}\,}$ donde m toma cualquier valor real.

Demostración

Recta que pasa por dos puntos

Si pasa por dos puntos ${\displaystyle (x_{1},y_{1})}$ y ${\displaystyle (x_{2},y_{2})}$, la ecuación de la recta puede expresarse como:

${\displaystyle y={\cfrac {y_{2}-y_{1}}{x_{2}-x_{1}}}\;(x-x_{1})+y_{1}}$

Demostración

Fórmulas para hallar "x" e "y" en una recta dada por coordenadas.

Tenemos una recta ${\displaystyle {\overline {AB}}}$ dada por dos puntos ${\displaystyle A(x_{A};y_{A})}$${\displaystyle B(x_{B};y_{B})}$, de la cual queremos hallar ${\displaystyle x}$ y ${\displaystyle y}$ a lo largo de la misma. Obtenemos la pendiente ${\displaystyle m_{\overline {AB}}}$y utilizamos las fórmulas respectivas para hallarlas:

${\displaystyle m_{\overline {AB}}={y_{B}-y_{A} \over x_{B}-x_{A}}}$

${\displaystyle x={y-y_{A} \over m_{\overline {AB}}}+x_{A}}$

${\displaystyle y=m_{\overline {AB}}(x-x_{A})+y_{A}}$

Donde:

${\displaystyle x}$ y ${\displaystyle y}$: ordenada y abcisas a hallarse;

${\displaystyle x_{A}}$, ${\displaystyle y_{A}}$, ${\displaystyle x_{B}}$, ${\displaystyle y_{B}}$: ordenadas y abcisas respectivas de los puntos A y B de la recta ${\displaystyle {\overline {AB}}}$;

${\displaystyle m_{\overline {AB}}}$: pendiente de la recta ${\displaystyle {\overline {AB}}}$.

Fórmulas para hallar el punto de intersección de dos rectas dadas por sus puntos de coordenadas.

Para obtener las coordenadas del punto de intersección ${\displaystyle (x_{I};y_{I})}$ de dos rectas ${\displaystyle {\overline {AB}}}$ y ${\displaystyle {\overline {CD}}}$, podemos utilizar la siguientes fórmulas.

${\displaystyle x_{I}={(m_{\overline {AB}}*x_{A})-y_{A}-(m_{\overline {AB}}*x_{C})+y_{C} \over m_{\overline {AB}}-m_{\overline {CD}}}}$

${\displaystyle y_{I}=m_{\overline {AB}}(x_{I}-x_{A})+y_{A}}$

Donde:

${\displaystyle x_{I}}$ y ${\displaystyle y_{I}}$: ordenada y abcisas de la intersección.

Recta que no pasa por el origen

En coordenadas polares una recta que pasa a una distancia d > 0, tiene una ecuación dada por:

${\displaystyle \rho (\theta )={\frac {d}{\cos(\theta -\theta _{0})}}}$

Donde la pendiente de la recta viene dada por ${\displaystyle 1/\tan \theta _{0}}$.

Rectas notables

Rectas perpendiculares.

• La ecuación de una recta vertical responde a la ecuación general ${\displaystyle x=x_{v}}$ (constante).

• La ecuación de una recta horizontal responde a la ecuación general ${\displaystyle y=y_{h}}$ (constante).

• Una recta trigonoidal que pase por el origen O (0, 0), cumplirá la condición b = 0, siendo su ecuación: ${\displaystyle y=(m)(x)\;}$.

• Recta secante

• Recta tangente

• Dos rectas cualesquiera:

${\displaystyle y=\left(m_{1}\right)\left(x\right)+b_{1}\!}$

${\displaystyle y=\left(m_{2}\right)\left(x\right)+b_{2}\!}$

serán paralelas si y solo si ${\displaystyle m_{1}=m_{2}\;}$. Además, serán coincidentes cuando: ${\displaystyle b_{1}=b_{2}\;}$

serán perpendiculares si y solo si ${\displaystyle m_{1}=-1/m_{2}\;}$, es decir: ${\displaystyle (m_{1})(m_{2})=-1\;}$

Rectas en el plano como espacio vectorial y afín

Mediante dos puntos del plano afín

Dado dos puntos en el plano, P y Q, sobre una recta, se puede describir cada punto de ésta (es decir toda la recta) mediante la ecuación:

${\displaystyle P+\lambda {\vec {PQ}}}$ donde ${\displaystyle \lambda }$ puede tomar cualquier valor.

Ejemplo

Dados ${\displaystyle P=(1,2)}$ y ${\displaystyle Q=(3,5)}$, entonces la recta son los puntos ${\displaystyle (x,y)}$ tales que ${\displaystyle x=1+\lambda (3-1)}$ y ${\displaystyle y=2+\lambda (5-2)}$.

Mediante un punto y un vector

Dado un punto y un vector en el plano, P y ${\displaystyle {\vec {v}}}$, queda totalmente definida una recta mediante la ecuación:

${\displaystyle P+\lambda {\vec {v}}}$ donde ${\displaystyle \lambda }$ puede tomar cualquier valor.

Ejemplo

Dados ${\displaystyle P=(5,-2)}$ y ${\displaystyle {\vec {v}}=(3,1)}$(llamado vector director), entonces la recta son los puntos ${\displaystyle (x,y)}$ tales que ${\displaystyle x=5+\lambda (3)}$ y ${\displaystyle y=-2+\lambda (1)}$.

Rectas notables

• La ecuación de una recta vertical poseería un vector director del tipo ${\displaystyle {\vec {v}}=(0,1)}$.
• La ecuación de una recta horizontal poseería un vector director del tipo ${\displaystyle {\vec {v}}=(1,0)}$.
• Una recta por el origen, es una recta que pasa por el origen de coordenadas con ${\displaystyle P=(0,0)\in r}$.
• Dadas dos rectas cualesquiera

${\displaystyle P+\lambda _{1}{\vec {v}}}$

${\displaystyle Q+\lambda _{2}{\vec {w}}}$

serán paralelas si y solo si ${\displaystyle {\vec {v}}=\alpha {\vec {w}}}$.

serán perpendiculares si y solo si ${\displaystyle {\vec {v}}}$ y ${\displaystyle {\vec {w}}}$ son perpendiculares, es decir su producto escalar es cero.

Rectas como producto escalar

Toda recta ya sea de forma implícita, explícita o vectorial se puede expresar como producto escalar de vectores:

${\displaystyle (x,y)=(b_{x},b_{y})+\lambda (u_{x},u_{y})\Leftrightarrow \lambda ={\frac {x-b_{x}}{u_{x}}}\;\;\;\;y\;\;\;\;\lambda ={\frac {y-b_{y}}{u_{y}}}\Leftrightarrow }$ ${\displaystyle {\frac {x-b_{x}}{u_{x}}}={\frac {y-b_{y}}{u_{y}}}\Leftrightarrow }$ ${\displaystyle {\frac {x}{u_{x}}}+{\frac {-y}{u_{y}}}={\frac {b_{x}}{u_{x}}}+{\frac {-b_{y}}{u_{y}}}\Leftrightarrow }$ ${\displaystyle (x,y)\cdot {\begin{pmatrix}{\frac {1}{u_{x}}}\\{\frac {-1}{u_{y}}}\end{pmatrix}}={\frac {b_{x}}{u_{x}}}+{\frac {-b_{y}}{u_{y}}}}$

es decir, renombrando las constantes:

${\displaystyle (x,y)\cdot {\begin{pmatrix}a\\b\end{pmatrix}}=c}$

• Si ${\displaystyle (x,y)\perp (a,b)\Rightarrow c=0}$ por tanto el vector ${\displaystyle (a,b)}$ es perpendicular a la recta ${\displaystyle ax+by=0}$ y a sus vectores directores, y por tanto a todas sus paralelas.

Ecuación de la recta en el espacio

Recta determinada mediante un sistema de ecuaciones

Sistema de 2 ecuaciones y 3 variables.

Recta en el espacio usando un sistema de 2 ecuaciones y 3 incógnitas:

${\displaystyle \left\{{\begin{matrix}x&+y&+z&=4\\x&-y&+3z&=7\end{matrix}}\right.}$

• Esta ecuación equivale a la intersección de dos planos en el espacio.

Recta determinada mediante vectores

Recta en el espacio usando un punto, ${\displaystyle p=(p_{x},p_{y},p_{z})}$, y un vector, ${\displaystyle u=(u_{x},u_{y},u_{z})}$:

${\displaystyle (x,y,z)=(p_{x},p_{y},p_{z})+\lambda (u_{x},u_{y},u_{z})}$

• Al vector ${\displaystyle u\,}$ se le llama vector director.

Posiciones relativas entre rectas

• Dos rectas serán paralelas si tiene vectores directores paralelos.
• Dos rectas serán coincidentes si comparten al menos dos puntos diferentes.
• Dos rectas se intersecan si no son paralelas y tienen un punto en común.
• Dos rectas serán coplanarias⁵ si están contenidas en algún plano.
  • Dos rectas son coplanarias si y solo si o bien son coincidentes o bien se intersecan o bien son paralelas.
• Dos rectas se cruzan^{nota 2} si no son paralelas y tienen puntos comunes.