Geometría elemental

teorema de Routh¹ determina la relación de áreas entre un triángulo dado y un triángulo formado por la intersección de tres cevianas (una por cada vértice).

El teorema de Routh permite calcular el área del triángulo ΔGHI (en rojo), formado por las tres cevianas AD, BE y CF.

Nomenclatura

Sea un triángulo cualquiera ΔABC (el exterior, amarillo en el gráfico), en cuyos lados AB, BC y CA se han marcado los puntos F, D y E, siendo estos tres últimos pies cualesquiera de las cevianas AD, BE y CF.

Los puntos I, G y H conforman al triángulo interior ΔIGH (color rojo el en el gráfico). Donde I, G y H son los puntos de intersección de las cevianas (AD con CF), (AD con BE) y (BE con CF).

${\displaystyle I=AD\cap CF,\quad G=AD\cap BE,\quad H=BE\cap CF}$

Denominando a las razones de los respectivos segmentos de cada lado como r, s y t:

${\displaystyle {\overline {AF}}/{\overline {BF}}=r}$

${\displaystyle {\overline {BD}}/{\overline {CD}}=s}$

${\displaystyle {\overline {CE}}/{\overline {AE}}=t}$

Llamando a las áreas de los triángulos ΔABC y ΔIGH respectivamente como A_ABC y A_IGH.

Enunciado del teorema

Con la nomenclatura antes mencionada, el teorema de Routh afirma que el área del triángulo ΔIGH es:

${\displaystyle A_{IGH}={\frac {(r\cdot s\cdot t-1)^{2}}{(s\cdot t+s+1)(r\cdot t+t+1)(r\cdot s+r+1)}}\;A_{ABC}.}$

El teorema de Ceva puede ser considerado como un caso especial del teorema de Routh. En el caso especial de que las tres cevianas AD, BE y CF se intersequen en un solo punto, entonces el área del triángulo ΔIGH es 0. Se puede concluir que ( r s t = 1 ), lo cual es justamente el enunciado del teorema de Ceva.

sector hiperbólico es una región del plano cartesiano {(x,y)} delimitada por los rayos desde el origen a dos puntos (a, 1/a) y (b, 1/b) y la hipérbola xy = 1.¹

En un sector hiperbólico en posición estándar a = 1 y b > 1 .

El área de un sector hiperbólico en posición estándar es el log_e b . (Demostración: Integrar bajo la curva 1/x entre 1 y b, y sumarle el área del triángulo {(0, 0), (1, 0), (1, 1)}, y restarle el área del triángulo {(0, 0), (b, 0), (b, 1/b)} )

Cuando un sector hiperbólico se encuentra en posición estándar el mismo se corresponde con un ángulo hiperbólico positivo.

 segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales.

Así, dado dos puntos A y B, se le llama segmento AB a la intersección de la semirrecta de origen A que contiene al punto B con la semirrecta de origen B que contiene al punto A. Los puntos A y B son extremos del segmento y los puntos sobre la recta a la que pertenece el segmento (la «recta sostén»), serán interiores o exteriores al segmento según pertenezcan o no a este . 

Segmentos consecutivos

Segmentos consecutivos.

Dos segmentos son consecutivos cuando tienen en común únicamente un extremo. Según pertenezcan o no a la misma recta, se clasifican en:

• Colineales, alineados o adyacentes.

91461990

Los segmentos como cantidades

El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total a+b es al segmento más largo a, como a es al segmento más corto b.

El conjunto de los segmentos métricos, constituye una magnitud, de la que los segmentos son cantidades. Es posible determinar entre ellos relaciones y efectuar las operaciones definidas para los elementos de una magnitud:

Comparación de segmentos

Postulado de las tres posibilidades (Ley de Tricotomía): Dados dos segmentos, debe verificarse una y solo una de las tres posibilidades siguientes:

• Los segmentos son iguales
• El primero es mayor que el segundo
• El primero es menor que el segundo

Posibilidades que se excluyen y se completan, es decir que al cumplirse una dejan de cumplirse las otras dos.

Igualdad de segmentos

La igualdad de segmentos, verificable por superposición, goza de las siguientes propiedades:

• Idéntica, reflexiva o refleja: Cualquier segmento es igual a sí mismo.
• Recíproca o simétrica: Si un segmento es congruente con otro, aquel es congruente con el primero.

Desigualdad

La desigualdad de segmentos, goza de la propiedad transitiva para las relaciones de mayor y de menor.

Operaciones

Se distinguen las siguientes operaciones:

Suma

La suma de varios segmentos consecutivos colineales, da por resultado el segmento determinado por los extremos no comunes de los segmentos considerados. Geométricamente, la suma de segmentos es otro segmento que se obtiene construyendo colinealmente segmentos ordenadamente congruentes con los dados, y procediendo como se indica al principio.

Suma de segmentos.

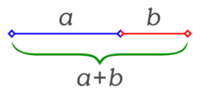
La suma de dos segmentos es otro segmento que tiene por inicio el origen del primer segmento y como final el final del segundo segmento.

La longitud del segmento suma es igual a la suma de las longitudes de los dos segmentos que lo forman.

La división de segmentos conmensurables es el algoritmo de Euclides.

 segmento
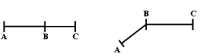
En la figura siguiente tienes la recta r sobre la que hemos señalado dos puntos A y B. Al trozo de recta entre A y B llamamos segmento.

Cuando veas la notación  se refiere al segmento existente entre A y B. Casi siempre, a los segmentos los designamos con letras mayúsculas.

15.4   Si en una recta fijas dos puntos ¿en cuántas partes has dividido a la recta?

Respuesta: En tres partes.

15.5  ¿Cuántas semirrectas y cuántos segmentos creamos al fijar dos puntos en una recta?

Respuesta: 2 semirrectas y un segmento.

Solución:
En la figura que tienes a continuación puedes ver:

1) Los puntos A y B.
2) Las semirrectas  m y n
3) El segmento AB

Las semirrectas m y n  tienen principio u origen pero no tienen fin.
La porción de recta (en color rojo) comprendida entre los puntos A y B es un segmento.

15.6  Si decimos que una semirrecta tiene un origen, el final ¿dónde se encuentra?

Respuesta: En el infinito, no tiene límite.

15.7  Dos semirrectas ¿pueden tener un punto común?

Respuesta: Sí, el punto origen de ambas.

15.8   ¿Cuántos puntos necesito para trazar una recta que los incluya?

Respuesta: Dos puntos.

15.9  ¿Existe alguna diferencia entre recta y semirrecta?

Respuesta: Sí, la recta no tiene ni principio ni fin, la semirrecta aunque tampoco tiene fin, sí tiene un origen.

15.10   Si unimos dos semirrectas opuestas ¿qué resultado obtenemos?
Respuesta: La recta.

simetría axial (también llamada rotacional, radial o cilíndrica) es la simetría alrededor de un eje. Es el punto de traslación y rotación de modo que un sistema tiene simetría axial o axisimetría cuando todos los semiplanos tomados a partir de cierta mediatriz y conteniéndolo presentan idénticas características.También puede decirse que es una isometría indirecta e involutiva.

Dada una recta se llama simetría axial de eje al movimiento que transforma a un punto P en otro punto P' verificando que:

• El segmento PP' es perpendicular a ${\displaystyle \scriptstyle e}$.
• Los puntos P y P' equidistan del eje ${\displaystyle \scriptstyle e}$.

Dicho de otra forma el eje ${\displaystyle \scriptstyle e}$ es la mediatriz del segmento OP'.

La simetría axial no solo se presenta entre un objeto y su reflexión, pues muchas figuras que mediante una línea pueden partirse en dos secciones que son simétricas con respecto a la línea. Estos objetos tienen uno (o más) ejes de simetría.

La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo.

A los puntos que pertenecen a la figura simétrica se les llama puntos homólogos, es decir, A’ es homólogo de A, B’ es homólogo de B, y C’ es homólogo de C. Además, las distancias existentes entre los puntos de la figura original son iguales que las distancias entre los puntos de la figura simétrica. En este caso: La simetría axial se puede dar también en un objeto con respecto de uno o más ejes de simetría.

Si se doblara la figura sobre el eje de simetría trazado, se podría observar con toda claridad que los puntos de las partes opuestas coinciden, es decir, ambas partes son congruentes.

Problema axisimétrico respecto a un eje, la situación en todos los semiplanos Π, como el de la figura es idéntica.

Física

Un cierto número de problemas físicos de interés, especialmente relacionados con la teoría de campos, los medios continuos o la teoría cuántica son más fáciles de resolver cuando los datos de partida tiene simetría axial, ya que la solución para ciertas magnitudes incógnitas también tendrá simetría axial. Eso permite reducir un problema con tres coordenadas espaciales a un problema de dos variables. Por ejemplo en varias áreas de la resolución de ciertos problemas requiere estudiar la ecuación de Poisson siguiente:

${\displaystyle {\frac {\partial ^{2}\varphi }{\partial x^{2}}}+{\frac {\partial ^{2}\varphi }{\partial y^{2}}}+{\frac {\partial ^{2}\varphi }{\partial z^{2}}}=\rho (\mathbf {x} )}$

Cuando la función "fuente" tiene simetría axial, es decir:

${\displaystyle \rho (x,y,z)=\rho (x\cos \alpha -y\sin \alpha ,y\cos \alpha +x\sin \alpha ,z)\,}$

El problema puede reformularse en términos de dos variables como:

${\displaystyle {\frac {\partial ^{2}{\tilde {\varphi }}}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial {\tilde {\varphi }}}{\partial r}}+{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial z^{2}}}={\tilde {\rho }}(r,z)}$

Donde:

${\displaystyle {\begin{cases}\rho (x,y,z)={\tilde {\rho }}({\sqrt {x^{2}+y^{2}}},z),&{\tilde {\rho }}(r,z)=\rho (r\cos \theta ,r\sin \theta ,z)\\\varphi (x,y,z)={\tilde {\varphi }}({\sqrt {x^{2}+y^{2}}},z),&{\tilde {\varphi }}(r,z)=\varphi (r\cos \theta ,r\sin \theta ,z)\end{cases}}}$

Teoría de grupos

Dado un problema geométrico o físico caracterizado por un cierto número de magnitudes escalares ${\displaystyle \phi (\mathbf {x} )}$ o propiedades tensoriales ${\displaystyle T(\mathbf {x} )\in {\mathcal {T}}_{q}^{p}(\mathbb {R} ^{n})}$ se dice que el problema tiene simetría axial si existen representaciones F_p,q del grupo SO(2):¹

${\displaystyle F_{p,q}:SO(2)\to {\mathcal {T}}_{q}^{p}(\mathbb {R} ^{n})\otimes {{\mathcal {T}}_{q}^{p}}^{*}(\mathbb {R} ^{n})}$

Tales que:

${\displaystyle [F_{p,q}(\mathbf {T} )](F_{1,0}(\mathbf {x} ))=\mathbf {T} (\mathbf {x} ),\quad \phi (F_{1,0}(\mathbf {x} ))=\phi (\mathbf {x} )}$

Esta última expresa la condición de que el hecho de rotar el sistema de ejes deja forminvariantes las cantidades básicas que caracterizan el problema.