Geometría elemental

El teorema del ángulo exterior es la Proposición 1.16 en los Elementos de Euclides que dice así:

Todo ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes. Dado: ∆ABC es un triángulo, y ACD es un ángulo exterior al mismo. Para probar: mACD = mABC + mBAC (aquí, mACD denota la medida del ángulo ACD) Prueba: Afirmación Razón En ∆ABC, ma + mb + mc = 180°------[1] La suma de los ángulos interiores de un triángulo es igual a 180° Também, mb + md = 180°-------[2] Definición de ángulos suplementarios ∴ ma + mc + mb = mb + md De [1] y [2] ∴ ma + mc + mb = mb + md ∴ md = ma + mc p.e. mACD = mABC + mBAC   La trilateración es un método matemático para determinar las posiciones relativas de objetos usando la geometría de triángulos de forma análoga a la triangulación. A diferencia de ésta, que usa medidas de ángulo (junto con al menos una distancia conocida para calcular la localización del sujeto), la trilateración usa las localizaciones conocidas de dos o más puntos de referencia, y la distancia medida entre el sujeto y cada punto de referencia. Para determinar de forma única y precisa la localización relativa de un punto en un plano bidimensional usando sólo trilateración, se necesitan generalmente al menos 3 puntos de referencia. Estando en B, queremos conocer su posición relativa a los puntos de referencia P1, P2, y P3 en un plano bidimensional. Al medir r1 se reduce nuestra posición a una circunferencia. A continuación, midiendo r2, la reducimos a dos puntos, A y B. Una tercera medición, r3, nos devuelve nuestras coordenadas en B. Una cuarta medición también puede hacerse para reducir y estimar el error. Derivación Puede hallarse una derivación de la solución de un problema de trilateración tridimensional tomando las fórmulas de tres esferas e igualándolas. Para hacer esto, debemos aplicar tres limitaciones a los centros de estas esferas; todas deben estar en el plano z=0, otra debe estar en el origen, y una tercera en el eje x. Es posible, sin embargo, trasladar cualquier conjunto de tres puntos para cumplir con estos límites, encontrar el punto solución, y luego invertir la traslación para encontrar el punto solución en el sistema de coordenadas original. Empezamos con tres esferas, ${\displaystyle r_{1}^{2}=x^{2}+y^{2}+z^{2}}$, ${\displaystyle r_{2}^{2}=(x-d)^{2}+y^{2}+z^{2},}$ y ${\displaystyle r_{3}^{2}=(x-i)^{2}+(y-j)^{2}+z^{2}}$, Restamos la segunda a la primera y resolvemos para x: ${\displaystyle x={\frac {r_{1}^{2}-r_{2}^{2}+d^{2}}{2d}}}$. Al sustituir esto en la fórmula de la primera esfera se produce la fórmula de un círculo, la solución a la intersección de las dos primeras esferas: ${\displaystyle y^{2}+z^{2}=r_{1}^{2}-{\frac {(r_{1}^{2}-r_{2}^{2}+d^{2})^{2}}{4d^{2}}}}$. Igualando esta fórmula a la fórmula de la tercera esfera, tenemos: ${\displaystyle y={\frac {r_{1}^{2}-r_{3}^{2}-x^{2}+(x-i)^{2}+j^{2}}{2j}}={\frac {r_{1}^{2}-r_{3}^{2}+i^{2}+j^{2}}{2j}}-{\frac {i}{j}}x}$. Ahora que tenemos las coordenadas x e y del punto solución, podemos simplemente despejar z de la fórmula de la primera esfera: ${\displaystyle z={\sqrt {r_{1}^{2}-x^{2}-y^{2}}}}$ Ahora tenemos la solución para los tres puntos x, y y z. Ya que z se expresa en forma de raíz cuadrada, es posible que el problema tenga por solución cero, uno o dos resultados. Animación del proceso geométrico realizado para determinar la posición de un punto mediante trilateración. Se necesita navegador que soporte SVG animados mediante SMIL. Esta última parte puede visualizarse como tomar el círculo formado por la intersección de la primera y segunda esferas y creando luego su intersección con la tercera. Si ese círculo queda totalmente fuera de la esfera, z es igual a la raíz cuadrada de un número negativo: no existe una solución real. Si ese círculo toca la esfera en exactamente un punto, z es igual a cero. Si, por último, el círculo toca la superficie de la esfera en dos puntos, entonces z es igual a más menos la raíz cuadrada de un número positivo. En el caso de no haber solución, no poco probable cuando los datos presentan ruido, la solución más aproximada es cero. Uno debe ser cuidadoso, no obstante, de hacer una prueba de control (sanity check en inglés) y asumir el valor de cero sólo cuando el error es apropiadamente pequeño. En el caso de dos soluciones, pueden usarse algunas técnicas para desambiguar entre las dos. Esto puede hacerse matemáticamente, mediante el uso de una cuarta esfera con su centro localizado fuera del plano formado por los centros de las otras tres, y determinando qué punto cae más cercano a la superficie de esta esfera. O puede hacerse lógicamente —por ejemplo, el GPS asume que el punto que cae dentro de la órbita de los satélites es el correcto cuando se enfrenta a esta ambigüedad, ya que es generalmente seguro asumir que el usuario no está nunca en el espacio, fuera de las órbitas de los satélites. Modelo de error Cuando el error de medida se introduce en el dibujo, las cosas se complican un poco. Si sabemos que la distancia desde P a un punto de referencia cae en un rango (un intervalo cerrado) [r1, r2], entonces sabemos que P cae en una banda circular entre los círculos con esos dos radios. Si conocemos un rango para otro punto, podemos tomar la intersección, que constituirá una o dos áreas delimitadas por arcos circulares. Un tercer punto normalmente la estrechará a una sola área, pero esta área puede ser aún de tamaño significativo; puntos de referencia adicionales pueden ayudar a disminuirla aún más, pero a medida que ésta disminuye más medidas perderán utilidad. En tres dimensiones, estamos en su lugar interseccionando shells esféricos con grosor, similares a bolas de jugar a los bolos. Este nuevo modelo enfatiza la importancia de elegir tres puntos que estén en direcciones muy diferentes —si los puntos están relativamente cerca unos de otros y a su vez lejos del punto a localizar, se requerirán medidas muy precisas para encontrar el punto usando trilateración. Aplicación La trilateración puede usarse en la detección del lugar de caída de un rayo. Los detectores que operan en un sistema de sincronización común pueden usar la variación del tiempo de llegada de las emisiones de radiofrecuencia que acompañan al rayo para determinar las distancias desde cada detector al mismo. Tales sistemas pueden ser útiles en silvicultura para la prevención de incendios y en el seguimiento de tormentas. Pero su empleo más habitual es el proceso de determinación de la posición empleado por el sistema GPS. 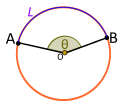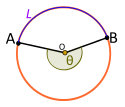Un ángulo central es un tipo de ángulo cuyo vértice es el centro O de una circunferencia, y cuyos lados son dos radios correspondientes a dos puntos distintos de la circunferencia A y B. Se dice que el ángulo central es subtendido por un arco entre esos dos puntos. La longitud del arco se corresponde con el producto del ángulo central (expresado en radianes) por el radio.1 El valor del ángulo central es también conocido como distancia angular del arco. El tamaño de un ángulo central Θ está comprendido entre 0°<Θ<360 0="" a="" adem="" al="" b="" c="" central="" convexo="" de="" debe="" definiendo="" definir="" dibujar="" el="" es="" especificar="" especificarse="" est="" los="" ncavo="" ngulo="" o="" puntos="" que="" radianes="" s="" se="" si="" un="" y=""> 180°). De forma equivalente, se debe especificar si el movimiento del punto A al punto B es dextrógiro o levógiro. Fórmulas Si los puntos de intersección A y B de los lados del ángulo con el círculo forman un diámetro, entonces Θ = 180° es un ángulo llano. (En radianes, Θ = π.) Sean L el arco menor de la circunferencia entre los puntos A y B; y R el radio de la circunferencia.2 Ángulo Central. Convexo. Es subtendido por el arco menor L Si el ángulo central Θ es subtendido por L, entonces ${\displaystyle 0^{\circ }<\Theta <180 annotation="" circ="" frac="" heta="\left({\frac" pi="" r="" right="">$ Prueba (para grados): La circunferencia de un círculo de radio R mide 2πR, y el arco menor L es (Θ/360°), la parte proporcional de la circunferencia completa (véase arco). Así: ${\displaystyle L={\frac {\Theta }{360^{\circ }}}\cdot 2\pi R\,\Rightarrow \,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }.}$ Ángulo Central. Cóncavo. No es subtendido por L Prueba (para radianes): La circunferencia de un círculo de radio R is 2πR, y el arco menor L es (Θ/2π) la parte proporcional de la circunferencia completa (véase arco). Así: ${\displaystyle L={\frac {\Theta }{2\pi }}\cdot 2\pi R\,\Rightarrow \,\Theta ={\frac {L}{R}}.}$ Si el ángulo central Θ no es subtendido por el arco menor L, entonces Θ es un ángulo de cóncavo y ${\displaystyle 180^{\circ }<\Theta <360 -="" annotation="" circ="" frac="" heta="\left(360-{\frac" pi="" r="" right="">$ Sea P el punto de corte de dos rectas tangentes a la circunferencia de centro O en A y en B. Entonces, los ángulos ∠ BOA (convexo) y ∠ BPA son suplementarios (suman 180°). Ángulo central de un polígono regular Un polígono regular de n lados tiene una circunferencia circunscrita en el que se encuentran todos sus vértices, y su centro es también el centro del polígono. El ángulo central del polígono regular se forma con los radios que unen el centro del polígono con dos vértices consecutivos. La medida de este ángulo es ${\displaystyle 2\pi /n.}$